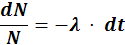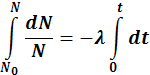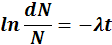Вывести закон радиоактивного распада построить график зависимости

Содержание

Вывести закон радиоактивного распада построить график зависимости
Физика. 11 класс
§ 39. Закон радиоактивного распада
Закон радиоактивного распада
Закон радиоактивного распада (вывод закона)

Вывести закон радиоактивного распада построить график зависимости

В природе существует большое число атомных ядер, которые могут спонтанно излучать элементарные частицы или ядерные фрагменты. Такое явление называется радиоактивным распадом . Этот эффект изучали на рубеже \(19-20\) веков Антуан Беккерель , Мария и Пьер Кюри , Фредерик Содди , Эрнест Резерфорд и другие ученые. В результате экспериментов, Ф.Содди и Э.Резерфорд вывели закон радиоактивного распада , который описывается дифференциальным уравнением \[\frac<><

> = — \lambda N,\] где \(N\) − количество радиоактивного материала, \(\lambda\) − положительная константа, зависящая от радиоактивного вещества. Знак минус в правой части означает, что количество радиоактивного материала \(N\left( t \right)\) со временем уменьшается (рисунок \(1\)).

Данное уравнение легко решить, и решение имеет вид: \[N\left( t \right) = C>.\] Чтобы определить постоянную \(C,\) необходимо указать начальное значение. Если в момент \(t = 0\) количество вещества было \(,\) то закон радиоактивного распада записывается в виде: \[N\left( t \right) = >.\]

Далее мы введем две полезных величины, вытекающие из данного закона.

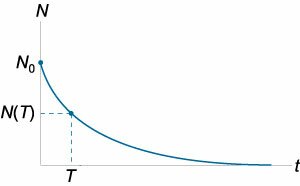
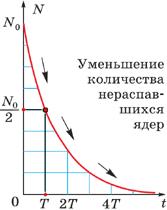
Периодом полураспада \(T\) радиоактивного материала называется время, необходимое для распада половины первоначального количества вещества. Следовательно, в момент \(T:\) \[N\left( T \right) = \frac<<>> <2>= >.\] Отсюда получаем формулу для периода полураспада: \[ <> = \frac<1><2>,>\;\; <\Rightarrow - \lambda T = \ln \frac<1> <2>= — \ln 2,>\;\; <\Rightarrow T = \frac<1><\lambda >\ln 2.> \] Среднее время жизни \(\tau\) радиоактивного атома определяется выражением \[\tau = \frac<1><\lambda >.\] Видно, что период полураспада \(T\) и среднее время жизни \(\tau\) связаны между собой по формуле: \[T = \tau \ln 2 \approx 0.693\,\tau \] Эти два параметра широко варьируются для различных радиоактивных материалов. Например, период полураспада полония-\(212\) меньше \(1\) микросекунды, а период полураспада тория-\(232\) превышает миллиард лет! Большой спектр изотопов с различными периодами полураспада был выброшен из атомных реакторов и охлаждающих бассейнов при авариях в Чернобыле и Фукусиме (рисунок \(2\)).

По истечении периода полураспада масса радиоактивного материала уменьшается в два раза. Поэтому, после \(3\) периодов полураспада масса материала будет составлять \(<\left( <\large\frac<1><2>\normalsize> \right)^3> = \large\frac<1><8>\normalsize\) от первоначального количества. Следовательно, через заданный промежуток времени масса вещества будет равна \(80\,\text<г>\cdot <\large\frac<1><8>\normalsize> = 10\,\text<г>.\)

Активность изотопа измеряется числом распада ядер за единицу времени, т.е. скоростью распада. Предположим, что \(d\) ядер распадаются за некоторый короткий период времени \(dt.\) Тогда активность изотопа \(A\) выражается формулой \[A = \frac<>><

>.\] Согласно закону радиоактивного распада, \[N\left( t \right) = >,\] где \(N\left( t \right)\) − количество еще нераспавшегося вещества. Поэтому, \[ <\left( t \right) = — N\left( t \right) > = <— > > = <\left( <1 - >> \right).> \] Дифференцируя последнее выражение по времени \(t,\) находим выражение для активности: \[A\left( t \right) = \frac<>><

> = \lambda >.\] Первоначальная активность изотопа составляла \[A\left( \right) = = \lambda .\] Следовательно, \[A\left( t \right) = >.\] Как видно, активность снижается со временем по такому же закону, как и количество еще нераспавшегося материала. Подставляя выражение для периода полураспада \(T = \large\frac<<\ln 2>><\lambda >\normalsize\) в последнюю формулу, получаем: \[A\left( t \right) = >\normalsize>>.\] Из последнего выражения легко найти значение \(T:\) \[ <>\normalsize>> = \frac<<>>,>\;\; <\Rightarrow - \frac<> = \ln \frac<<>>,>\;\; <\Rightarrow \frac<> = \ln \frac<<>>,>\;\; <\Rightarrow T = \frac<><<\ln \frac<<>>>>.> \] В нашем случае период полураспада изотопа составляет \[ ><<\ln \frac<<>>>> > = <\frac<<30\ln 2>><<\ln \frac<<100>><<90>>>> > \approx <\frac<<30 \cdot 0.93>><<\ln 1.11>> > \approx <197.3\,\text<дня>.> \]

Источник

Физика. 11 класс

§ 39. Закон радиоактивного распада

При всем разнообразии реакций самопроизвольного (спонтанного) распада ядер в этом процессе наблюдается общая закономерность, которую можно описать математически. Интересно, что зависимость количества распавшихся ядер от времени задается одной и той же функцией для различных ядер, участвующих в распаде. Перейдем к количественному описанию процессов радиоактивного распада.

Большинство изотопов любого химического элемента превращается в более устойчивые изотопы путем радиоактивного распада. Каждый радиоактивный элемент распадается со своей, присущей только ему «скоростью». При этом для каждого радиоактивного ядра существует характерное время, называемое периодом полураспада , спустя которое в исходном состоянии остается половина имевшихся ядер. Таким образом, периодом полураспада называется промежуток времени, за который распадается половина начального количества радиоактивных ядер. Другая половина ядер превращается в более устойчивые изотопы посредством распада.
Отметим, что период полураспада не зависит от того, в каком состоянии находится вещество: твердом, жидком или газообразном. Кроме того, период полураспада радиоактивного вещества не зависит от его количества, от времени, места и условий, в которых оно находится. Поэтому количество радиоактивных ядер «тогда» и «сейчас» непосредственно определяет промежуток времени , прошедший с момента уменьшения числа ядер от до .
Невозможно точно предсказать, когда произойдет распад данного ядра. Однако можно оценить среднее число ядер, которые распадутся за данный промежуток времени. Таким образом, закон радиоактивного распада является статистическим и он справедлив только при достаточно большом количестве радиоактивных ядер.

Для записи закона радиоактивного распада будем считать, что в начальный момент времени ( ) число радиоактивных ядер . Через промежуток времени, равный периоду полураспада, это число будет , еще через такой же промежуток времени — (рис. 218). Спустя промежуток времени, равный n периодам полураспада , радиоактивных ядер останется:

Это соотношение выражает закон радиоактивного распада, который можно сформулировать следующим образом:

число нераспавшихся радиоактивных ядер убывает с течением времени по закону, представленному соотношением (1).

Закон радиоактивного распада позволяет найти число нераспавшихся ядер в любой момент времени. Полученное выражение хорошо описывает распад радиоактивных ядер, если их количество достаточно велико.
Приведем экспериментальные результаты, которые показывают, что при малом количестве радиоактивных ядер это выражение неприменимо. На рисунке 219 изображен график распада 47 ядер изотопа фермия , период полураспада которого . Из рисунка 219 видно, что пока ядер было достаточно много — от 47 до 12, то показательная функция хорошо описывала закон распада. Однако при меньшем числе ядер истинная зависимость существенно отличается от показательной функции.
Периоды полураспада некоторых радиоактивных изотопов веществ приведены в таблице 11.

Таблица 11. Периоды полураспада радиоактивных изотопов веществ
Вещество	Период полураспада
30,17 лет
5,3 года
8,04 суток
24 390 лет
1600 лет
3,8 суток
700 млн лет
4,5 млрд лет

Впервые процесс радиоактивного распада для измерения промежутков времени был использован в 1904 г . Резерфордом. По отношению концентрации урана и его дочернего продукта распада (гелия) он определил возраст урановой породы. Эта работа положила начало ядерной геохронологии — определению возраста различных минералов Земли по радиоактивным долгоживущим веществам. В дальнейшем исследование процессов ядерного синтеза позволило перейти к ядерной космохронологии, т.е. к определению продолжительных промежутков времени, прошедших с момента образования элементов в масштабах Галактики и Вселенной. В основу ядерной космохронологии положена неизменность «скорости» радиоактивного распада.

В 1927 г . американский ученый Г. Блюмгарт, используя изотоп , впервые определил скорость кровотока у людей.

В 1934 г . венгерский ученый Дьердь фон Хевеши, используя дейтерий, впервые установил, что в организме человека вода полностью обновляется в течение 14 суток.

В 1943 г. Дьердь фон Хевеши была присуждена Нобелевская премия по химии «за работу по использованию изотопов в качестве меченых атомов при изучении химических процессов».

Источник

Закон радиоактивного распада

Появление «ручных» сцинтилляционных счетчиков и, главным образом, счётчиков Гейгера–Мюллера, которые помогли автоматизировать подсчёты частиц (см. § 15-е), привело физиков к важному выводу. Любой радиоактивный изотоп характеризуется самопроизвольным ослабеванием радиоактивности, выражающимся в уменьшении количества распадающихся ядер в единицу времени.

Построение графиков активности различных радиоактивных изотопов приводило учёных к одной и той же зависимости, выражающейся показательной функцией (см. график). По горизонтальной оси отложено время наблюдения, а по вертикальной – количество нераспавшихся ядер. Кривизна линий могла быть различной, однако сама функция, которой выражались описываемые графиками зависимости, оставалась одной и той же:

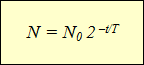N – количество нераспавшихся ядер
N0 – начальное количество ядер
t – время наблюдения, с
T – период полураспада, с

Эта формула выражает закон радиоактивного распада: количество нераспавшихся с течением времени ядер определяется как произведение начального количества ядер на 2 в степени, равной отношению времени наблюдения к периоду полураспада, взятой с отрицательным знаком.

Как выяснилось в ходе опытов, различные радиоактивные вещества можно охарактеризовать различным периодом полураспада – временем, за которое количество ещё нераспавшихся ядер уменьшается вдвое (см. таблицу).

Йод-129	15 млн лет	Углерод-14	5,7 тыс лет
Йод-131	8 дней	Уран-235	0,7 млрд лет
Йод-135	7 часов	Уран-238	4,5 млрд лет

Период полураспада – общепринятая физическая величина, характеризующая скорость радиоактивного распада. Многочисленные опыты показывают, что даже при очень длительном наблюдении за радиоактивным веществом его период полураспада постоянен, то есть не зависит от числа уже распавшихся атомов. Поэтому закон радиоактивного распада нашёл применение в методе определения возраста археологических и геологических находок.

Метод радиоуглеродного анализа. Углерод – очень распространённый на Земле химический элемент, в состав которого входят стабильные изотопы углерод-12, углерод-13 и радиоактивный изотоп углерод-14, период полураспада которого составляет 5,7 тысяч лет (см. таблицу). Живые организмы, потребляя пищу, накапливают в своих тканях все три изотопа. После прекращения жизни организма поступление углерода прекращается, и с течением времени его содержание убывает естественным путём, за счёт радиоактивного распада. Поскольку распадается только углерод-14, с течением веков и тысячелетий изменяется соотношение изотопов углерода в ископаемых останках живых организмов. Измерив эту «углеродную пропорцию», можно судить о возрасте археологической находки.

Метод радиоуглеродного анализа применим и для геологических пород, а также для ископаемых предметов быта человека, но при условии, что соотношение изотопов в образце не было нарушено за время его существования, например, пожаром или действием сильного источника радиации. Неучёт подобных причин сразу после открытия этого метода приводил к ошибкам на несколько веков и тысячелетий. Сегодня применяются «вековые калибровочные шкалы» для изотопа углерода-14, исходя из его распределения в долгоживущих деревьях (например, в американской тысячелетней секвойе). Их возраст можно подсчитать весьма точно – по годовым кольцам древесины.

Предел применения метода радиоуглеродного анализа в начале XXI века составлял 60 000 лет. Для измерения возраста более древних образцов, например горных пород или метеоритов, используют аналогичный метод, но вместо углерода наблюдают за изотопами урана или других элементов в зависимости от происхождения исследуемого образца.

Источник

Закон радиоактивного распада (вывод закона)

Закон радиоактивного распада определяет среднее число атомов, распадающихся за определенный промежуток времени. Допустим, что в радиоактивном препарате в произвольный момент времени t₀ имелось N₀ нераспавшихся радиоактивных атомов. Чем больше общее число радиоактивных атомов (N), тем больше и число распавшихся:

Из-за самопроизвольного и хаотического распада радиоактивных атомов можно считать, что число распавшихся атомов в интервале от t до t + dt пропорционально времени dt: dN

или dN = −λ · Ndt

где, как мы уже знаем, λ – коэффициент пропорциональности, называемый постоянной радиоактивного распада. Знак минус в правой части означает, что происходит уменьшение числа нераспавшихся атомов.

Разделим правую и левую часть в уравнении на число радиоактивных атомов (N), получим:

проинтегрировав это равенство получим:

отсюда число нераспавшихся атомов радиоактивного вещества равно:

Число распавшихся радиоактивных атомов можно определить из закона радиоактивного распада:

Продолжительность существования радионуклида обычно выражается периодом полураспада T_1/2. T_1/2 – строго постоянная величина для каждого радионуклида и, так же как и постоянная распада, характеризует его временную устойчивость.

Период полураспада T_1/2 – время, в течение которого число атомов радионуклида, а, следовательно, и его активность уменьшаются в результате распада вдвое.

Период полураспада связан с постоянной распада, получим соотношение, связывающее величину периода полураспада и постоянную распада.

По определению, период полураспада – это время за которое распадается половина всех ядер радиоактивного вещества, следовательно:

прологарифмировав это выражение, получим

(1.3)

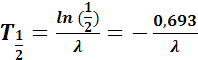
Из полученного выражения следует физический смысл периода полураспада: какое бы количество определенного радиоактивного препарата не было бы взято, половина его претерпит радиоактивный распад за одно и то же время.

Источник