- Законы Ньютона
- Что такое сила
- Смысл законов Ньютона
- Первый закон Ньютона
- Второй закон Ньютона
- Формула второго закона Ньютона с пояснениями
- Третий закон Ньютона
- Закон движения тела: определение, формулы
- О каких типах движения пойдет речь?
- Равномерное движение, или состояние покоя
- Перемещение по прямой с ускорением
- Прямолинейное ускоренное (замедленное) движение с наличием начальной скорости
- Движение по окружности
- Вращение вокруг оси с постоянной скоростью
- Вращение вокруг оси с ускорением
- Движение по эллиптической траектории на примере планет Солнечной системы
Законы Ньютона
Ньютон первым обратил внимание на силу, как причину, по которой тела приходят в движение и меняют свою скорость.
Раздел механики, изучающий силы, называется динамикой. По-гречески «динамис», значит «сила».
Что такое сила
Тела действуют друг на друга с помощью сил.
Сила – это мера взаимодействия тел. Измеряя силу, мы измеряем величину взаимного действия тел. В обыденной жизни мы говорим: «как сильно» одно тело действует на другое тело.
Смысл законов Ньютона
Ньютон, в своих законах динамики, хотел сказать следующее:
- В I законе: Если сила не действует, скорость не меняется. Импульс тела тоже не меняется.
- Во II законе: Если сила действует, скорость меняется. Импульс тела, также, меняется, появляется ускорение.
- В III законе: Взаимодействуют два тела — возникают две силы. Они по модулю равны, а по направлению противоположны.
Примечание:
Выражение «векторы равны по модулю», понимаем так: «длины векторов одинаковые».
Перед изучением законов Ньютона рекомендую вспомнить, что такое инерциальные системы отсчета (откроется в новой вкладке).
Первый закон Ньютона
Словесная формулировка первого закона Ньютона:
В инерциальной системе отсчета тело свою скорость не меняет, если на него не действуют другие тела (или действие других тел скомпенсировано).
Формула:
\( F = 0 \) – сила на тело не действует (Может быть и так: на тело действуют несколько сил, но их действие компенсируется);
\( a = 0 \) – ускорение отсутствует;
\( v = const \) – скорость тела не изменяется (остается одной и той же);
\( p = const \) – импульс тела не изменяется (остается одним и тем же);
Важно! По первому закону Ньютона, «двигаться с одной и той же скоростью по прямой» и «покоиться» — это равнозначные виды движения.
Значит, если на тело не действуют другие тела (силы), то
- тело будет двигаться с одной и той же скоростью по прямой, если оно так двигалось до этого,
- или будет продолжать покоиться, если покоилось в прошлом.
Второй закон Ньютона
Сформулируем словами второй закон Ньютона:
Ускорение, приобретаемое телом,
прямо пропорционально
приложенной силе
и обратно пропорционально
массе этого тела.
Формула второго закона Ньютона с пояснениями
\( a \left( \frac<\text<м>>
\( m \left( \text <кг>\right) \) – масса тела
\( F \left( H \right) \) – сила, которую приложили к телу
Примечание: Ускорение отвечает на вопрос: «Как быстро меняется скорость тела?». Значит, если изменяется хотя бы одна из характеристик вектора скорости, ускорение есть. А если скорость не изменяется, ускорения нет \( \vec < a >= 0 \)
Ускорение прямо пропорционально силе:
Чем больше сила, тем больше ускорение тела, тем быстрее тело меняет скорость.
Ускорение обратно пропорционально массе:
Чем больше месса тела, тем труднее изменить его скорость.
Формулу второго закона часто записывают в векторном виде:
Мы можем заменить местами правую и левую части, в таком случае получим:
Расшифруем эту запись: Возьмем вектор «F», умножим его на скаляр (1/m) и получим новый вектор «a».
Дробь \( \displaystyle \frac<1>
Примечания:
- Вместо слов «направлены в одну и ту же сторону» физики пользуются термином «сонаправлены». Лично мне удобнее пользоваться первой формулировкой.
- Часто применяют еще один вид записи, его называют так: «Второй закон Ньютона в импульсной форме».
Третий закон Ньютона
Пусть одно тело действует на второе тело. Тогда это второе тело будет в ответ действовать на первое.
Словами третий закона Ньютона можно сформулировать так:
Силы взаимного действия по модулю равны, а направлены противоположно. Они лежат на прямой, которая соединяет центры тел, действующих друг на друга.
\( F_ <12>\left( H \right) \) – сила, с которой первое тело действует на второе тело.
\( F_ <21>\left( H \right) \) – сила, с которой второе тело отвечает первому.
Пояснить формулу можно с помощью такого рисунка:
Обратите внимание, что длины красного и черного векторов равны.
Не важно, перед каким из векторов находится знак «минус». Этот знак показывает, что векторы направлены в противоположные стороны. Поэтому, формулу третьего закона Ньютона можно записать и так:
Примечания:
- Если перед каким-либо вектором записан знак «минус», то этот вектор развернут в противоположную от выбранной нами сторону.
- Между векторами находится знак равенства. Это значит, что длины векторов одинаковые (векторы по модулю равны).
Советую прочитать еще две статьи. Так как для решения задач кроме знания трех законов Ньютона нужно дополнительно уметь:
- находить проекции вектора на оси и
- составлять векторные силовые уравнения (ссылки открываются в новых вкладках).
Источник
Закон движения тела: определение, формулы
Каждый обращал внимание на все многообразие видов движения, с которыми он сталкивается в своей жизни. Однако любое механическое движение тела сводится к одному из двух типов: линейное или вращательное. Рассмотрим в статье основные законы движения тел.
О каких типах движения пойдет речь?
Как было отмечено во введении, все виды движения тела, которые рассматриваются в классической физике, связаны либо с прямолинейной траекторией, либо с круговой. Любые другие траектории можно получить благодаря комбинации этих двух. Далее в статье будут рассмотрены следующие законы движения тела:
Равномерное движение, или состояние покоя
Вам будет интересно: Преподаватели СПБГУ: педагогический состав, факультеты, направления
Этим движением с научной точки зрения начал интересоваться впервые Галилей в конце XVI — начале XVII века. Изучая инерционные свойства тела, а также введя понятие о системе отсчета, он догадался, что состояние покоя и равномерного движения — это одно и то же (все зависит от выбора объекта, относительно которого рассчитывают скорость).
Вам будет интересно: Характеристика движения под углом к горизонту: формулы, решение задачи с лучником
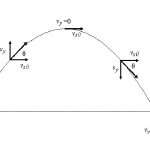
Впоследствии Исаак Ньютон сформулировал свой первый закон движения тела, согласно которому скорость последнего является постоянной величиной всегда, когда нет внешних сил, изменяющих характеристики движения.
Равномерное прямолинейное перемещение тела в пространстве описывается следующей формулой:
Где s — расстояние, которое преодолеет тело за время t, двигаясь со скоростью v. Это простое выражение также записывается в следующих формах (все зависит от величин, которые известны):
v = s / t; t = s / v
Перемещение по прямой с ускорением
Согласно второму закону Ньютона, наличие внешней силы, действующей на тело, неминуемо приводит к появлению ускорения у последнего. Из определения ускорения (быстрота изменения скорости) следует выражение:
Вам будет интересно: Тюркизмы в русском языке: понятие, история появления, звучание и примеры
a = v / t или v = a * t
Если действующая на тело внешняя сила будет оставаться постоянной (не будет изменять модуля и направления), то ускорение также не изменится. Такой тип движения называется равноускоренным, где ускорение выступает коэффициентом пропорциональности между скоростью и временем (скорость растет линейно).
Для этого движения пройденный путь рассчитывается с помощью интегрирования скорости по времени. Закон движения тела для пути при равноускоренном перемещении приобретает форму:
Самым распространенным примером этого движения является падение любого предмета с высоты, при котором сила тяжести сообщает ему ускорение g = 9,81 м/с2.
Прямолинейное ускоренное (замедленное) движение с наличием начальной скорости
По сути, речь идет о комбинации двух видов перемещения, рассмотренных в предыдущих пунктах. Представим простую ситуацию: автомобиль ехал с некоторой скоростью v0, затем водитель нажал на тормоза, и транспортное средство через некоторое время остановилось. Как описать движение в этом случае? Для функции скорости от времени справедливо выражение:
Здесь v0 — начальная скорость (до торможения авто). Знак минус говорит о том, что внешняя сила (трения скольжения) направлена против скорости v0.
Как и в предыдущем пункте, если взять интеграл по времени от v(t), то получаем формулу для пути:
s = v0 * t — a * t2 / 2
Отметим, что по этой формуле вычисляется только путь торможения. Чтобы узнать расстояние, пройденное автомобилем за все время его движения, следует найти сумму двух путей: для равномерного и для равнозамедленного движения.
В примере описанном выше, если бы водитель нажал не на педаль тормоза, а на педаль газа, тогда в представленных формулах поменялся бы знак «-» на «+».
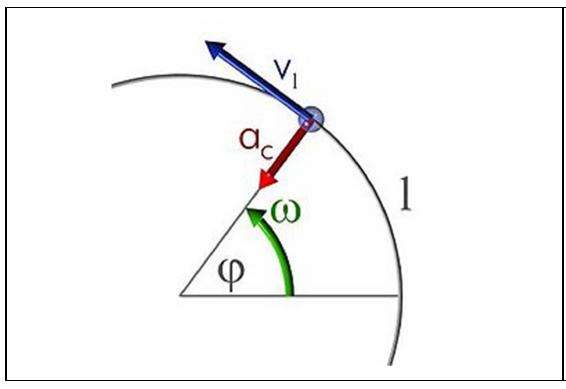
Движение по окружности
Любое движение по окружности не может происходить без ускорения, поскольку даже при сохранении модуля скорости изменяется ее направление. Ускорение, которое связано с этим изменением, называется центростремительным (именно оно искривляет траекторию тела, превращая ее в окружность). Модуль этого ускорения вычисляют так:
ac = v2 / r, r — радиус
В этом выражении скорость может зависеть от времени, как это происходит в случае равноускоренного движения по окружности. В последнем случае ac будет быстро расти (квадратичная зависимость).
Центростремительное ускорение определяет силу, которую нужно прикладывать, чтобы удерживать тело на круговой орбите. Примером являются соревнования по метанию молота, когда спортсмены прикладывают значительные усилия, чтобы раскрутить снаряд до его метания.
Вращение вокруг оси с постоянной скоростью
Этот вид движения идентичен предыдущему, только описывать его принято не с использованием линейных физических величин, а с применением угловых характеристик. Закон вращательного движения тела, когда угловая скорость не изменяется, в скалярной форме записывается так:
Здесь L и I — моменты импульса и инерции, соответственно, ω — угловая скорость, которая с линейной связана равенством:
Величина ω показывает, на сколько радиан повернется тело за секунду. Величины L и I имеют такой же смысл, как импульс и масса для прямолинейного движения. Соответственно, угол θ, на который повернется тело за время t, вычисляется так:
Примером этого типа движения является вращение маховика, находящегося на коленчатом вале в двигателе автомобиля. Маховик — это массивный диск, которому очень тяжело придать какое-либо ускорение. Благодаря этому он обеспечивает плавность изменения крутящего момента, который передается от двигателя к колесам.
Вращение вокруг оси с ускорением
Если к системе, которая способна вращаться, прикладывать внешнюю силу, то она начнет увеличивать свою угловую скорость. Такая ситуация описывается следующим законом движения тела вокруг оси вращения:
F * d = I * dω / dt
Здесь F — внешняя сила, которая приложена к системе на расстоянии d от оси вращения. Произведение в левой части равенства носит название момента силы.
Для равноускоренного движения по окружности получаем, что ω зависит от времени следующим образом:
ω = α * t, где α = F * d / I — угловое ускорение
В этом случае угол поворота за время t можно определить, проинтегрировав ω по времени, то есть:
Если же тело уже вращалось с некоторой скоростью ω0, а затем начал действовать внешний момент силы F*d, то по аналогии с линейным случаем можно записать такие выражения:
θ = ω0 * t + α * t2 / 2
Таким образом, появление внешнего момента сил является причиной наличия ускорения в системе с осью вращения.
Для полноты информации отметим, что изменить скорость вращения ω можно не только с помощью внешнего момента сил, но и благодаря изменению внутренних характеристик системы, в частности ее момента инерции. Эту ситуацию видел каждый человек, который наблюдал за вращением фигуристов на льду. Группируясь, спортсмены увеличивают ω за счет уменьшения I, согласно простому закону движения тела:
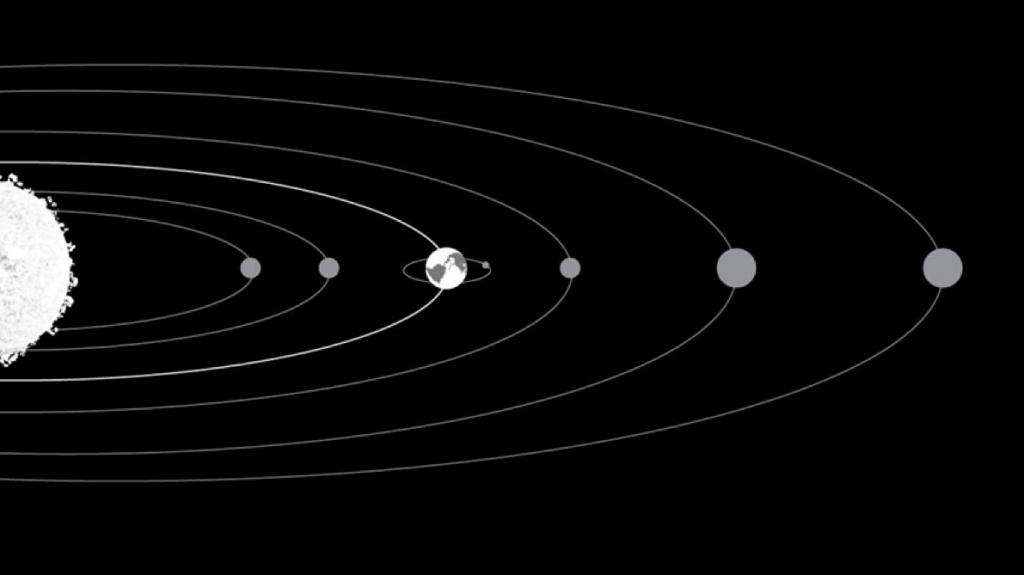
Движение по эллиптической траектории на примере планет Солнечной системы
Как известно, наша Земля и другие планеты Солнечной системы вращаются вокруг своей звезды не по окружности, а по эллиптической траектории. Впервые математические законы для описания этого вращения сформулировал знаменитый немецкий ученый Иоганн Кеплер в начале XVII века. Используя результаты наблюдений своего учителя Тихо Браге за движением планет, Кеплер пришел к формулировке своих трех законов. Они формулируются следующим образом:
T2 / a3 = С = const
Впоследствии Исаак Ньютон, используя эти законы движения тел (планет), сформулировал свой знаменитый закон всемирной гравитации, или тяготения. Применяя его, можно показать, что константа C в 3-м законе Кеплера равна:
C = 4 * pi2 / (G * M)
Где G — гравитационная универсальная константа, а M — масса Солнца.
Отметим, что движение по эллиптической орбите в случае действия центральной силы (тяготения) приводит к тому, что линейная скорость v постоянно меняется. Она максимальна, когда планета находится ближе всего к звезде, и минимальна вдали от нее.
Источник
