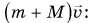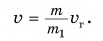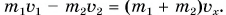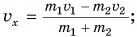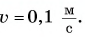- Законы Ньютона
- Что такое сила
- Смысл законов Ньютона
- Первый закон Ньютона
- Второй закон Ньютона
- Формула второго закона Ньютона с пояснениями
- Третий закон Ньютона
- Законы сохранения в физике — основные понятия, формулы и определения с примерами
- Законы сохранения в механике
- Импульс тела и импульс системы тел
- Закон сохранения импульса и реактивное движение
- Механическая работа и мощность
Законы Ньютона
Ньютон первым обратил внимание на силу, как причину, по которой тела приходят в движение и меняют свою скорость.
Раздел механики, изучающий силы, называется динамикой. По-гречески «динамис», значит «сила».
Что такое сила
Тела действуют друг на друга с помощью сил.
Сила – это мера взаимодействия тел. Измеряя силу, мы измеряем величину взаимного действия тел. В обыденной жизни мы говорим: «как сильно» одно тело действует на другое тело.
Смысл законов Ньютона
Ньютон, в своих законах динамики, хотел сказать следующее:
- В I законе: Если сила не действует, скорость не меняется. Импульс тела тоже не меняется.
- Во II законе: Если сила действует, скорость меняется. Импульс тела, также, меняется, появляется ускорение.
- В III законе: Взаимодействуют два тела — возникают две силы. Они по модулю равны, а по направлению противоположны.
Примечание:
Выражение «векторы равны по модулю», понимаем так: «длины векторов одинаковые».
Перед изучением законов Ньютона рекомендую вспомнить, что такое инерциальные системы отсчета (откроется в новой вкладке).
Первый закон Ньютона
Словесная формулировка первого закона Ньютона:
В инерциальной системе отсчета тело свою скорость не меняет, если на него не действуют другие тела (или действие других тел скомпенсировано).
Формула:
\( F = 0 \) – сила на тело не действует (Может быть и так: на тело действуют несколько сил, но их действие компенсируется);
\( a = 0 \) – ускорение отсутствует;
\( v = const \) – скорость тела не изменяется (остается одной и той же);
\( p = const \) – импульс тела не изменяется (остается одним и тем же);
Важно! По первому закону Ньютона, «двигаться с одной и той же скоростью по прямой» и «покоиться» — это равнозначные виды движения.
Значит, если на тело не действуют другие тела (силы), то
- тело будет двигаться с одной и той же скоростью по прямой, если оно так двигалось до этого,
- или будет продолжать покоиться, если покоилось в прошлом.
Второй закон Ньютона
Сформулируем словами второй закон Ньютона:
Ускорение, приобретаемое телом,
прямо пропорционально
приложенной силе
и обратно пропорционально
массе этого тела.
Формула второго закона Ньютона с пояснениями
\( a \left( \frac<\text<м>>
\( m \left( \text <кг>\right) \) – масса тела
\( F \left( H \right) \) – сила, которую приложили к телу
Примечание: Ускорение отвечает на вопрос: «Как быстро меняется скорость тела?». Значит, если изменяется хотя бы одна из характеристик вектора скорости, ускорение есть. А если скорость не изменяется, ускорения нет \( \vec < a >= 0 \)
Ускорение прямо пропорционально силе:
Чем больше сила, тем больше ускорение тела, тем быстрее тело меняет скорость.
Ускорение обратно пропорционально массе:
Чем больше месса тела, тем труднее изменить его скорость.
Формулу второго закона часто записывают в векторном виде:
Мы можем заменить местами правую и левую части, в таком случае получим:
Расшифруем эту запись: Возьмем вектор «F», умножим его на скаляр (1/m) и получим новый вектор «a».
Дробь \( \displaystyle \frac<1>
Примечания:
- Вместо слов «направлены в одну и ту же сторону» физики пользуются термином «сонаправлены». Лично мне удобнее пользоваться первой формулировкой.
- Часто применяют еще один вид записи, его называют так: «Второй закон Ньютона в импульсной форме».
Третий закон Ньютона
Пусть одно тело действует на второе тело. Тогда это второе тело будет в ответ действовать на первое.
Словами третий закона Ньютона можно сформулировать так:
Силы взаимного действия по модулю равны, а направлены противоположно. Они лежат на прямой, которая соединяет центры тел, действующих друг на друга.
\( F_ <12>\left( H \right) \) – сила, с которой первое тело действует на второе тело.
\( F_ <21>\left( H \right) \) – сила, с которой второе тело отвечает первому.
Пояснить формулу можно с помощью такого рисунка:
Обратите внимание, что длины красного и черного векторов равны.
Не важно, перед каким из векторов находится знак «минус». Этот знак показывает, что векторы направлены в противоположные стороны. Поэтому, формулу третьего закона Ньютона можно записать и так:
Примечания:
- Если перед каким-либо вектором записан знак «минус», то этот вектор развернут в противоположную от выбранной нами сторону.
- Между векторами находится знак равенства. Это значит, что длины векторов одинаковые (векторы по модулю равны).
Советую прочитать еще две статьи. Так как для решения задач кроме знания трех законов Ньютона нужно дополнительно уметь:
- находить проекции вектора на оси и
- составлять векторные силовые уравнения (ссылки открываются в новых вкладках).
Источник
Законы сохранения в физике — основные понятия, формулы и определения с примерами
Содержание:
Три закона Ньютона являются основой механики. Выдающийся американский физик XX ст. P Фейнман в своих знаменитых «Фейнмановских лекциях» отметил, что вся классическая механика содержится в этих законах. C их помощью в принципе можно решить любую задачу о движении тел с малыми скоростями.
Значение законов Ньютона заключается не только в этом. Они позволили создать стройную физическую теорию механического движения тел, ввести такие фундаментальные физические величины, как энергия и импульс, установить для них законы сохранения, являющиеся фундаментальными законами природы. C помощью этих законов в динамике решаются задачи, когда силы взаимодействия тел неизвестны. Например, при столкновении тел трудно определить значения сил взаимодействия между ними.
Законы сохранения в механике
Все изменения, наблюдаемые нами в природе, -результат взаимодействия между телами. Взаимодействия бывают электромагнитные, гравитационные и ядерные. Их интенсивность зависит не только от их природы, но и от расстояний между телами, их характеристик.
При определенных условиях один вид взаимодействия может быть интенсивнее другого. Так, на больших расстояниях существенным является гравитационное взаимодействие, в то время как ядерное будет существенным только на расстояниях, соизмеримых с размерами ядра атома.
Одновременно сделать расчеты всех взаимодействий тяжело, да и не всегда нужно. Поэтому ученые, как правило, рассматривают физические явления, пренебрегая некоторыми второстепенными взаимодействиями. Например, при расчетах силы трения, действующей на колеса автомобиля, существенной является сила притяжения Земли, а действием Луны можно пренебречь.
Ученые, рассматривая физические явления, как правило, пренебрегают второстепенными взаимодействиями.
При расчетах движения межпланетного корабля в пределах Солнечной системы нельзя пренебречь действием на корабль Солнца и планет, а вот действие далеких звезд можно не принимать во внимание.
Таким образом, в общей картине природы рассматривается лишь некоторая совокупность физических тел, условно изолированных от окружающей среды и объединенных общими признаками.
Группа объединенных по общим признакам тел, на которые не действуют другие тела или их действие несущественно в данных условиях, называется замкнутой (изолированной) системой.
Замкнутость системы — понятие относительное и определяется задачами, которые ставятся перед исследованиями, и уровнем развития их экспериментального или теоретического методов решения. Если система по определенным соображениям объявляется замкнутой, то она не становится абсолютно изолированной, «вне природы», в ней действуют те же физические законы. Это подтверждается многочисленными исследованиями, свидетельствующими об однородности пространства. Ни одной точке пространства нельзя дать преимущество по сравнению с другими точками, а протекание физических явлений не изменяется в случае перехода из одной точки пространства в другую. Поэтому не случайно закон гравитационного взаимодействия называется всемирным.
Наличие однородности в полной мере присуще и времени. Течение времени в разных точках пространства происходит одинаково. Поэтому некоторые физические величины в замкнутых системах остаются неизменными, например масса, энергия, импульс, т. е. подчиняются законам сохранения. В механике основными такими законами являются закон сохранения энергии и закон сохранения импульса.
Импульс тела и импульс системы тел
Еще в XVII в. в механике появилось понятие «количество движения». В настоящее время количество движения тела называют импульсом тела (от латинского impulses — толчок). Чему он равен? Как его можно изменить?
В механике Ньютона импульсом тела называется векторная величина, равная произведению массы тела на скорость его движения:
Импульс тела направлен так же, как скорость движения тела. Единица импульса в СИ — I килограмм-метр в секунду
Из определения следует, что импульс зависит и от скорости, и от массы. Например, импульс груженого самосвала БЕЛАЗ гораздо больше импульса движущегося с такой же скоростью автомобиля (рис. 225).
Согласно первому закону Ньютона скорость движения тела, на которое не действуют силы или действие сил скомпенсировано, постоянна. Значит, в этом случае постоянен и его импульс. Изменить импульс тела можно, только приложив к нему силу.
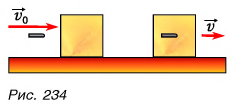
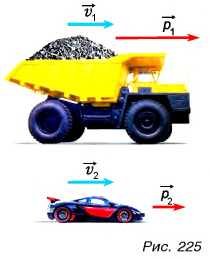
Рассмотрим пример. Тележку массой т, имеющую начальную скорость 
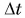
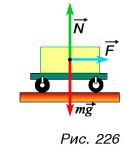
Найдем результирующую силу, действующую на тележку. Силами сопротивления можно пренебречь, сила реакции N и сила тяжести mg (рис. 226) компенсируют друг друга. Тогда по второму закону Ньютона
Подставляя в эту формулу ускорение 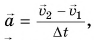
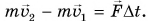
Величину 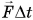
Импульс силы — это векторная величина, равная произведению силы на время ее действия.
Формула (2) выражает закон изменения импульса тела.
Изменение импульса тела равно импульсу результирующей всех сил, приложенных к нему.
Из данного закона следует:
- изменение импульса тела
направлено так же, как результирующая сила F;
- изменение импульса тела тем больше, чем больше приложенная к нему сила и чем продолжительнее время ее действия.
Формулу (2) можно записать в виде
Для любознательных:
Равенство 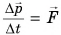
Закон изменения импульса объясняет целый ряд явлений повседневной жизни.
Проделаем простой опыт. Возьмем две нити: обычную 1 и резиновую 2 (рис. 227) одинаковой прочности и длины. Привяжем их к одинаковым грузам и дадим грузам возможность падать с одинаковой высоты. Нить 1 порвется, а нить 2 — нет (рис. 227). Почему это происходит?
Дело в том, что промежуток времени торможения At для груза на обычной нити 1 был во много раз меньше, чем для груза на резиновой, легко деформируемой нити 2. Из формулы (3) следует, что сила F тем больше, чем меньше 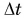
Это необходимо учитывать в технике. Нельзя делать резких рывков при подъеме грузов и при буксировке транспортных средств. Может произойти обрыв троса.
Чтобы избежать тяжелых последствий при столкновениях, следует уменьшить силу или увеличить время, за которое импульс уменьшится до нуля. Для этой цели вагоны снабжают буферными пружинными амортизаторами (рис. 228), автомобили — бамперами, ремнями безопасности, автоматически срабатывающими воздушными подушками (рис. 229).
И наоборот, для получения больших сил используют удар, при котором импульс изменяется за очень малый промежуток времени At (см. формулу (3)). Примерами служат забивание свай падающим молотом (рис. 230), разрушающее действие пуль, снарядов и т. д.
Мы рассмотрели изменение импульса одного тела. А как изменяется суммарный импульс нескольких тел?
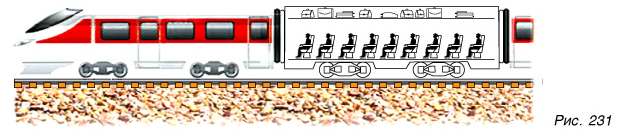
В механике группу из нескольких тел называют механической системой. Тела, не входящие в систему, называются внешними телами.
Например, механической системой является пассажирский вагон (рис. 231). В механическую систему «вагон» входят: корпус вагона, люди, находящиеся в вагоне, багаж и т. д. Внешними телами будут: Земля, локомотив, рельсы, остальные вагоны поезда и т. д.
Силы взаимодействия тел системы друг с другом называют внутренними. Например, в системе «вагон» внутренней будет сила, с которой багаж давит на полку, и сила, с которой полка действует на багаж. Силы, действующие на тела системы со стороны внешних тел, называют внешними силами. Например, сила тяжести, с которой Земля действует на багаж, — это внешняя сила.
Каждое из тел механической системы имеет свой импульс. Векторная сумма импульсов всех тел, входящих в систему, называется импульсом механической системы:
где п — количество тел системы.
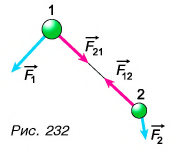
Рассмотрим систему из двух тел (1 и 2) (рис. 232). Силы их взаимодействия 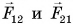
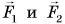
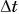
- •для тела 1:
- •для тела 2:
- •для всей системы:
По третьему закону Ньютона силы взаимодействия тел
А если в механическую систему входит больше двух тел? Сумма всех внутренних сил будет по-прежнему равна нулю, а изменение импульса механической системы
где 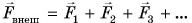
Формула (4) выражает закон изменения импульса механической системы.
Изменение импульса механической системы равно импульсу результирующей внешних сил.
Таким образом, только внешние силы могут вызвать изменение импульса механической системы. Внутренние силы не изменяют импульс механической системы в целом, но могут изменить импульс отдельных тел системы.
Ответьте самостоятельно: какая сила увеличивает импульс вагона на участке разгона? Какие силы уменьшают импульс вагона при его торможении? Могут ли пассажиры, находящиеся в вагоне, вызвать изменение импульса механической системы «вагон»?
Главные выводы:
- Импульс тела — это векторная величина, равная произведению массы тела на скорость его движения.
- Направление импульса тела совпадает с направлением его скорости.
- Изменение импульса тела равно импульсу результирующей всех сил, приложенных к нему.
- Изменить импульс механической системы могут только внешние силы. Это изменение равно импульсу результирующей внешних сил.
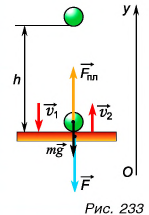
Пример №1
Шарик массой 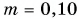
Решение
Так как на шарик во время удара действуют сила тяжести и сила, приложенная к нему со стороны плиты, то изменение импульса шарика за время удара 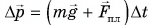
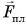
где 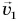
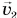
В проекции на ось Оу.
Так как шарик свободно падал без начальной скорости с высоты h, то 
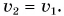
По третьему закону Ньютона средняя сила, с которой шарик во время удара действовал на плиту, 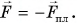
Сила, с которой шарик во время удара действовал на плиту, направлена по вертикали вниз. Модуль средней силы удара в 81 раз больше, чем вес покоящегося шарика.
Закон сохранения импульса и реактивное движение
Знаменитый французский философ и математик Рене Декарт (1596— 1650) утверждал: «Во Вселенной есть известное количество движения, которое никогда не изменяется. И если одно тело приводит в движение другое, то оно теряет столько своего движения, сколько его сообщает». Как вывести это утверждение из закона изменения импульса?
В предыдущем параграфе мы доказали, что импульс системы тел может измениться только под действием внешних сил:
А если результирующая внешних сил 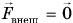
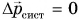
Векторное равенство (2) выражает закон сохранения импульса. Импульс механической системы сохраняется, если результирующая внешних сил, действующих на нее, равна нулю.
В каких случаях можно применять закон сохранения импульса? Прежде всего — когда на систему вообще не действуют внешние силы. Такие системы называют замкнутыми. Импульс замкнутой системы не изменяется (сохраняется), как и утверждал Декарт.
Реальные механические системы не бывают замкнутыми. На все окружающие нас тела действует Земля, на Землю действует Солнце и т. д. Однако закон сохранения импульса можно применять и для незамкнутых систем, если:
- •внешние силы действуют, но их результирующая
;
- •системы «замкнуты» в данном направлении, т. е. проекция
на это направление равна нулю. В этом случае сохраняется проекция импульса
на это направление;
- •внешние силы малы или ими можно пренебречь.
Например, закон сохранения импульса применяют при решении задач о столкновениях тел, выстрелах и т. д., когда в течение крайне малых промежутков времени внутри системы возникают огромные силы. Рассмотрим пример. Деревянный кубик массой М лежит на горизонтальном столе. В кубик попадает пуля массой 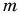
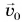
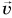
Замкнута ли система «кубик + пуля»? Нет. Но сила тяжести системы скомпенсирована силой реакции опоры, а сила трения кубика о стол мала. Значит, величиной 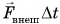
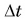
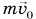
Значит, скорость кубика вместе с пулей после удара
Соударение, в результате которого тела объединяются и ведут себя как единое целое, называют абсолютно неупругим ударом.
Рассмотренный пример — частный случай такого удара. Другими примерами являются соединение вагонов при сценке, слипание пластилиновых шариков при соударении и т. д.
Рассмотрим теперь пример, в котором происходит не объединение, а разделение частей системы.
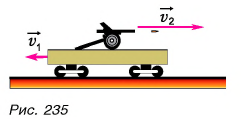
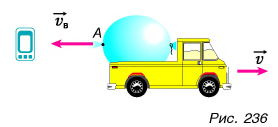
На горизонтальном рельсовом пути стоит платформа (рис. 235) с закрепленной на ней пушкой. Установка может свободно катиться по рельсам. Ствол орудия горизонтален. Пушка производит выстрел. Платформа приобретает скорость, направленную противоположно скорости снаряда.
Как найти скорость 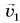
Так как импульс системы до выстрела был равен нулю, то после выстрела:
где 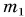
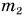
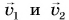
Почему платформа пришла в движение? Потому что пороховые газы, образовавшиеся в канале ствола при выстреле, действовали как на снаряд, так и на пушку. Сила, приложенная к пушке, вызвала движение платформы с пушкой в направлении, противоположном движению снаряда («отдачу»). Аналогичное явление можно наблюдать на простом опыте. Прикрепим к игрушечному автомобилю надутый воздушный шарик (рис. 236). Проколем его в точке А иглой. Образуется струя воздуха, вырывающегося из шарика, и автомобиль приходит в движение. Оно возникло при отделении от тела его части со скоростью, не равной нулю. Его называют реактивным движением, а силу, ускоряющую тело, — реактивной силой.
Реактивная сила возникает при отделении от тела какой-либо его части со скоростью, не равной нулю (относительно тела).
Устройство, создающее реактивную силу, называется реактивным двигателем.
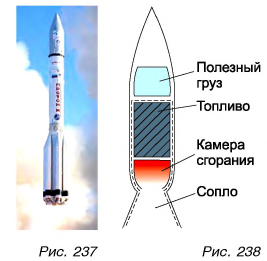
Реактивными двигателями оснащены скоростные самолеты, современные космические корабли (рис. 237). Упрощенная схема реактивного двигателя показана на рисунке 238.
Какую скорость 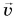
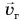
По закону сохранения импульса из формулы (5) находим модуль скорости, приобретаемой ракетой:
Значит, ракета набирает тем большую скорость, чем больше скорость истечения газов из ее сопла и чем меньше масса ракеты. Отсюда понятна выгода использования многоступенчатых ракет (рис. 238). После выгорания топлива в ступени ее отделяют. Масса ракеты уменьшается, что облегчает ее дальнейший разгон. С помощью многоступенчатых ракет выводят на орбиту искусственные спутники Земли, исследуют околоземное и межпланетное космическое пространство.
Первый в мире искусственный спутник Земли был запущен в 1957 г. в СССР. Первый орбитальный полет человека вокруг Земли совершил летчик-космонавт Ю. Гагарин в 1961 г. Американские астронавты Н. Армстронг и Э. Олдрин в 1969 г. первыми высадились на поверхность Луны.
Ракетно-космические исследования стали неотъемлемой частью современной цивилизации. Среди космонавтов есть уроженцы Беларуси: П. И. Климук, В. В. Коваленок, О. В. Новицкий. С космодрома «Байконур» 22 июля 2012 г. был запущен Белорусский космический аппарат (БКА) — спутник массой 400 кг. Он обеспечивает дистанционное зондирование территории Беларуси путем съемки из космоса.
Главные выводы:
- Если результирующая внешних сил равна нулю, то импульс системы сохраняется.
- Закон сохранения импульса можно применить к незамкнутым системам, если влиянием внешних сил можно пренебречь.
- Реактивная сила возникает при отделении от тела какой-либо его части с не равной нулю скоростью.
Пример №2
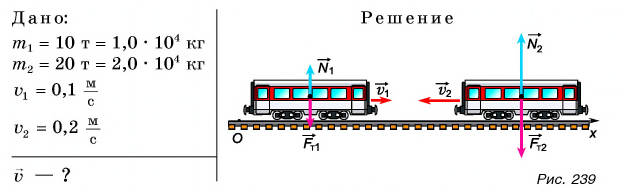
Два вагона массами 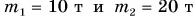
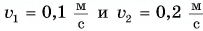
На систему из двух вагонов (рис. 239) действуют внешние силы: силы тяжести 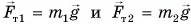
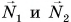
В итоге сумма внешних сил, действующих на вагоны, равна нулю. Значит, к системе из двух вагонов можно применить закон сохранения импульса: 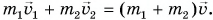
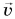
Отсюда
Знак «—» указывает на то, что после автосцепки вагоны будут двигаться противоположно направлению оси Ох.
Ответ: скорость v направлена противоположно оси Ох;
Механическая работа и мощность
В 7-м классе вы познакомились с физической величиной, называемой «механическая работа». Вы узнали, что; в случае когда направление силы F совпадает с направлением движения, работа, которую совершает эта сила, определяется по формуле:
А если сила направлена под углом к перемещению? Как определить работу в этом случае?
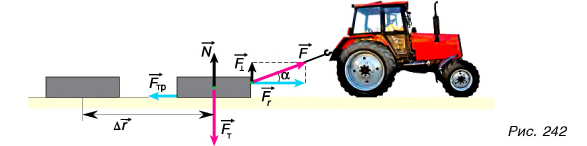
Рассмотрим пример. Трактор передвигает бетонный блок, действуя на него силой 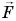
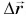
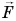
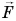
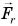
В направлении силы 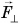
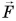
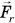
Так как 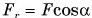
Механическая работа равна модулю силы, умноженному на модуль перемещения и на косинус угла между силой и перемещением.
Работа — скалярная величина.
Единицей работы в СИ является 1 джоуль (1 Дж). Он равен работе, совершаемой силой 1 ныотон при перемещении тела на 1 метр в направлении этой силы (1 Дж = 1 Н • м).
Работа силы может быть положительной, отрицательной или равной нулю. Это зависит от угла между силой и перемещением. Из формулы (1) следует:
- •если угол а острый, то cos а > 0 и работа положительна;
- •если прямой — равна нулю (cosа = 0);
- •если тупой — отрицательна (cos а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник


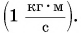
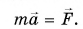

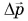 направлено так же, как результирующая сила F;
направлено так же, как результирующая сила F;



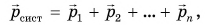
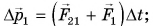
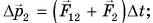
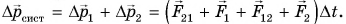
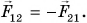
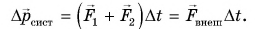


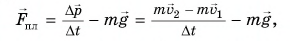
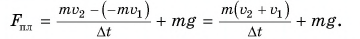
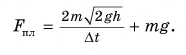
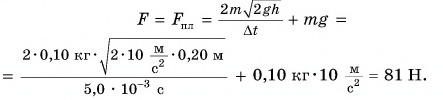


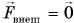 ;
;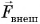 на это направление равна нулю. В этом случае сохраняется проекция импульса
на это направление равна нулю. В этом случае сохраняется проекция импульса 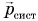 на это направление;
на это направление;