Вывести последовательность фибоначчи питон

Числа Фибоначчи: циклом и рекурсией

Числа Фибоначчи – это ряд чисел, в котором каждое следующее число равно сумме двух предыдущих.

Иногда ряд начинают с нуля.

В данном случае мы будем придерживаться первого варианта.

Вычисление n-го числа ряда Фибоначчи с помощью цикла while

Присвоим переменным fib1 и fib2 значения двух первых элементов ряда, то есть единицы.

Получим от пользователя номер элемента, значение которого требуется вычислить. Присвоим номер элемента переменной n .

Поскольку значения первых двух элементов ряда Фибоначчи нам уже известны и вычисления начинаем с третьего, количество проходов по телу цикла должно быть на 2 меньше значения n , то есть n — 2 .

Если пользователь вводит 1 или 2, тело цикла ни разу не выполняется, на экран выводится исходное значение fib2 .

В теле цикла выполнять следующие действия:

1. Сложить fib1 и fib2 , присвоив результат переменной для временного хранения данных, например, fib_sum .
2. Переменной fib1 присвоить значение fib2 .
3. Переменной fib2 присвоить значение fib_sum .

После окончания работы цикла вывести значение fib2 на экран.

Пример выполнения программы:

Компактный вариант кода:

Вывод чисел Фибоначчи циклом for

В данном случае выводится не только значение искомого элемента ряда Фибоначчи, но и все числа до него включительно. Для этого вывод значения fib2 помещен в цикл.

Рекурсивное вычисление n-го числа ряда Фибоначчи

1. Если n = 1 или n = 2, вернуть в вызывающую ветку единицу, так как первый и второй элементы ряда Фибоначчи равны единице.
2. Во всех остальных случаях вызвать эту же функцию с аргументами n — 1 и n — 2. Результат двух вызовов сложить и вернуть в вызывающую ветку программы.

Допустим, n = 4. Тогда произойдет рекурсивный вызов fibonacci(3) и fibonacci(2). Второй вернет единицу, а первый приведет к еще двум вызовам функции: fibonacci(2) и fibonacci(1). Оба вызова вернут единицу, в сумме будет два. Таким образом, вызов fibonacci(3) возвращает число 2, которое суммируется с числом 1 от вызова fibonacci(2). Результат 3 возвращается в основную ветку программы. Четвертый элемент ряда Фибоначчи равен трем: 1 1 2 3.

Источник

Числа Фибоначчи

Ряд чисел Фибоначчи представляет собой последовательность. Первый и второй элементы последовательности равны единице. Каждый последующий элемент равен сумме двух предыдущих. Рассмотрим разные способы нахождения элементов по номеру и генерацию списка с помощью Python 3.

Введение

Расчет ряда чисел Фибонначчи – один из лучших примеров программ на Python, использующих рекурсию. Хотя наиболее частый пример, рекурсии – это расчет факториала.

Рассмотрим варианты получения ряда Фибоначчи на Python 3:

• С помощью рекурсии.
• Используя оператор цикла.

Также сгенерируем список чисел и создадим генератор с помощью которого можно поочередно получать числа.

Будем искать с помощью цикла for. В переменных prew и cur будут предыдущий элемент последовательности и текущий, их проинициализируем в 1. Если пользователь запросит первый или второй элемент, то мы так и не попадём внутрь тела цикла. И будет выведена единица из переменной cur .

Если же запросят 3-ий или какой либо последующий элемент последовательности Фибоначчи, то мы зайдем в цикл. Во временную переменную tmp сохраним следующее число последовательности. После этого заполним prew и cur новыми значениям. Когда пройдет нужное количество итераций, выведем значение cur в консоль.

В предыдущем коде нам пришлось воспользоваться переменной tmp . Но можно код внутри цикла переписать следующим образом:

Теперь вместо трех строк кода получилась одна строка! И пропала необходимость использования дополнительной переменной.

В этом примере мы использовали цикл for , но можно эту программу реализовать, немного изменив код, с помощью цикла while .

Рекурсия

В случае с рекурсией напишем функцию, аргументом которой будет требуемое число ряда Фибоначчи. Текущему значению последовательности cur вначале присвоим 1. После этого воспользуемся условным оператором языка Python – if . В нем проверим аргумент функции. Если он больше 2, то функция вызовет саму себя и вычислит предыдущее значение ряда, а так же то, которое было еще раньше и запишет в переменную cur их сумму.

Конечно, пример с рекурсией интересен. Но он будет работать гораздо медленнее.

А если вы решите вычислить, допустим 1000-ый элемент последовательности. Используя цикл, мы его очень быстро рассчитаем. А вот в случае с рекурсией получим ошибку превышения максимального количества рекурсий:

Генератор списка

Если мы захотим инициализировать список рядом Фибоначчи, то это можно сделать следующим образом:

Здесь fibonacci(10) это генератор объекта ряда размерностью 10. При каждом последующем вызове он будет с помощью yield возвращать очередной элемент. Мы создаём из него список. Затем выводим список в консоль с помощью функции print .

Если нам надо будет поочередно получать числа ряда, а не держать в памяти сразу весь список, то можно поступить следующим образом:

Здесь мы создали с помощью Python 3 генератор чисел Фибоначчи. При помощи функции next мы получаем поочередно числа ряда.

Источник

Числа Фибоначчи в языке программирования Python: как произвести расчет

Бывают такие случаи, когда необходимо генерировать или вычислять числа Фибоначчи при помощи Python. Числа Фибоначчи — это рядность целых последовательных чисел. Числовой ряд строится по следующему принципу: каждое число является суммой предыдущих двух чисел.

Последовательность числ ового ряда Фибоначчи выглядит так: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и так далее до бесконечности. Числа Фибоначчи известны не только своей грациозной последовательностью и красивыми графиками, но и одной особенностью: при делении двух соседних чисе л ( большее на меньшее) получается примерно одинаковый результат — 1,618. Такая пропорция названа «золотым сечением». Чуть позже люди стали замечать, что «золотое сечение» прослеживается везде в нашем окружении :

пропорциональный рост граней снежинок;

расположение лепестков в цветах и листьев в папоротнике;

рост « чешуек » ананаса;

раковины улиток завиты по этому сечению;

пропорции человеческого тела, например , рост разделить на расстояние от ступней и до пояса;

Кстати, уче н ые выяснили, что люди, чья внешность кажется наиболее приятной , несут больше соотношений «золотого сечения» в своем строении.

Цикл «while» в Python и числа Фибоначчи

Наиболее популярным методом вычисления числа Фибоначчи является использование цикла. Представим, что вам нужно вычислить число Фибоначчи с индексом «n». Что мы имеем:

fnum1 и fnum2 нам известны, значения первых двух чисел Фибоначчи равны 1;

количество проходов по циклу будет на 2 пункта меньше, потому что первые два числа нам известны, то есть «n-2»;

в цикле должны выполняться следующие действия: fnum1+fnum2, а полученную сумму необходимо будет сохранять в переменную, допустим , в fibSum;

после суммирования переменной fnum1 присваивается значение предыдущего fnum2, а fnum2 присваивает значение fnumSum, освобождая переменную для следующего суммирования;

цикл повторяется «n-2» количеств о раз;

после окончания прохождения цикла на экран необходимо вывести значение последней переменной fnum2.

Как это реализуется:

n = input (“ Введите номер числа Фибоначчи: “)

fnumSum = fnum1 + fnum2

print(“Число Фибоначчи под вашим номером: “, fnum2)

Результат программы будет следующим:

Введите номер числа Фибоначчи: 13

Число Фибоначчи под вашим номером: 233

Цикл «for» в Python и числа Фибоначчи

Цикл «for» в Python позволяет вывести не только конкретное число Фибоначчи, но и все предшествующие числа, то есть целый ряд чисел. Чтобы у нас это получилось , мы вывод значения «fsum2» поместим в цикл.

Как это реализуется:

fnum1 = fnum2 = 1

n = intput (“Введите номер числа Фибоначчи: “)

print (fnum1, fnum2, end= )

for i in range(2, n):

fnum1, fnum2 = fnum2, fnum1 + fnum2

print(“Ряд чисел Фибоначчи до указанного номера: “, fnum2, end= )

Программа нам выдаст следующий результат:

Введите номер числа Фибоначчи: 13

Ряд чисел Фибоначчи до указанного номера: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233

Заключение

Числа Фибоначчи можно просчитать при помощи циклов «for» или «while». Иногда для генерации чисел используют рекурсию, однако она имеет ряд ограничений и работает медленнее, чем представленные функции.

Мы будем очень благодарны

если под понравившемся материалом Вы нажмёте одну из кнопок социальных сетей и поделитесь с друзьями.

Источник

Рекурсивный метод нахождения чисел Фибоначчи

Описание задачи

Программа принимает на вход число членов последовательности Фибоначчи и при помощи рекурсии вычисляет все числа, входящие в эту последовательность.

Решение задачи

1. Принимаем на вход число членов последовательности и записываем его в отдельную переменную.
2. Это число передается в качестве аргумента в рекурсивную функцию, которая будет вычислять n -й член последовательности.
3. В качестве базового условия принимаем то обстоятельство, что число членов последовательности Фибоначчи не может быть меньше единицы либо равно ей. При наступление этого условия рекурсия останавливается.
4. В противном случае функция вызывается вновь следующим образом: в качестве аргумента нашей рекурсивной функции передается введенное число, уменьшенное на единицу, и к этому прибавляется эта же функция с аргументом, уменьшенным уже на 2.
5. Каждый вызов функции возвращает одно число, которое мы потом выводим на экран.

Исходный код

Ниже дан исходный код, который осуществляет вывод всех членов последовательности Фибоначчи заданного размера. Результаты работы программы также даны ниже.

Объяснение работы программы

1. Пользователь вводит число и оно записывается в переменную n .
2. Передаем число n в качестве аргумента в рекурсивную функцию, которая вычисляет n-ый член последовательности.
3. Так как первый член последовательности Фибоначчи по определению не может быть меньше 1, в качестве базового условия принимаем n . Когда оно выполняется, рекурсия прерывается.
4. В противном случае функция вызывается вновь следующим образом: fibonacci(n-1) + fibonacci(n-2) .
5. Результаты выводятся на экран при помощи цикла for .

Результаты работы программы

Примечания переводчика

Данный пример приведен только с целью подробного ознакомления с алгоритмами рекурсии. Как вы можете заметить, данный код крайне неэффективен и не экономичен с вычислительной точки зрения, поскольку для вычисления n-го члена последовательности нам необходимо вычислять все предыдущие. И так мы делаем ровно n раз. Когда числа n являются большими, данный код абсолютно не применим. И, разумеется, для решения этой задачи есть другие, более эффективные, алгоритмы.

Источник

Мемоизация, рекурсия и цикл for в Python

В этой статье мы подробно разберем, как создать последовательность Фибоначчи. Решение данной задачи мы покажем с использованием трех разных методов. Рассмотрим мемоизацию, рекурсию и цикл for в Python.

Как вы, вероятно, знаете, последовательность Фибоначчи образуется следующим образом. Мы складываем первое и второе число, 0 и 1, чтобы получить третье число в последовательности (0 + 1 = 1). Затем мы складываем второе и третье число, чтобы получить 4-е число в последовательности (1 + 1 = 2). И так проделываем для каждого последующего числа Фибоначчи.

Код, который мы будем рассматривать, вы можете писать в Jupyter, Colab или любой IDE или текстовом редакторе, который вам удобен.

Вычисление n-го члена последовательности Фибоначчи с помощью цикла for

Напишем базовую программу, используя цикл for . Логика последовательности проста, мы уже обсудили ее выше.

Временная сложность решения с помощью цикла for — O(n), а пространственная сложность – O(1) или константа. Правда, на самом деле все несколько сложнее.

«Если ваше число меньше, чем 94, и вы используете 64-битное число, тогда алгоритм ведет себя, как имеющий линейную сложность. Но для N > 94 он начинает вести себя, как алгоритм с квадратичной сложностью», — из ответа Майкла Векслера на сайте Quora.

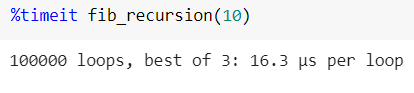
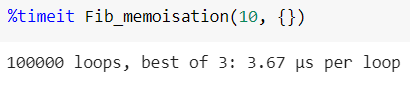
Запустим этот код с помощью модуля Python %timeit . Это позволит замерить время выполнения, избежав ряда распространенных ловушек.

Для того, чтобы высчитать 10-е число Фибоначчи, потребовалось по 675 наносекунд на каждую итерацию цикла.

Вычисление n-го члена последовательности Фибоначчи с помощью рекурсии

Теперь давайте реализуем последовательность Фибоначчи с помощью рекурсии. Рекурсивные функции вызывают себя повторно, пока не достигнут базового случая. Таким образом, рекурсия создает древовидную структуру.

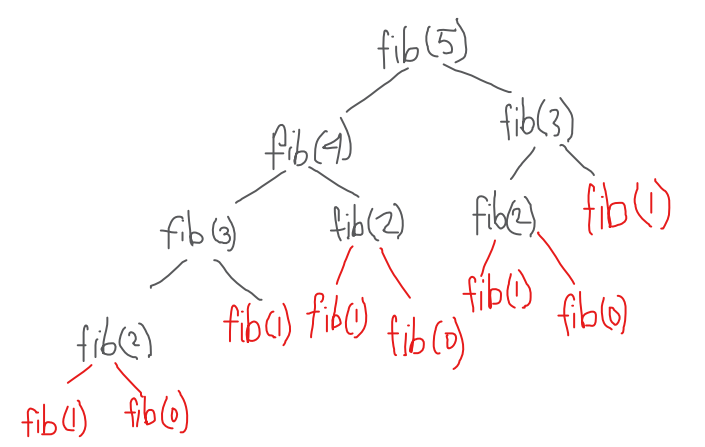
Если мы возьмем первые 5 чисел Фибоначчи, то в результате рекурсии получится вот такое дерево.

Пространственная сложность в данном случае — O(n), а временная сложность — O(2 n ). Так происходит, потому что у корневого узла есть 2 дочерних узла (fib(4) и fib(3)) и 4 внука. И, как видите, у каждого узла есть 2 дочерних элемента. Кроме того, вы могли заметить, что правое поддерево меньше, чем левое. Так что, на самом деле время выполнения составляет примерно O(1,6 n ).

Базовый случай: Fibonacci(2) = Fib(1) + Fib(0) = 1 + 0 = 1

Вычисление n-го члена последовательности Фибоначчи при помощи рекурсии определенно быстрее, чем с помощью цикла for.

Вычисление n-го члена последовательности Фибоначчи с использованием мемоизации

Мемоизация – это метод, который может значительно улучшить производительность рекурсивной функции за счет уменьшения вычислительных затрат. Он сохраняет результаты дорогостоящих вызовов функций в массиве или словаре и при вызове с такими же входными данными возвращает кэшированные результаты.

Давайте ещё раз посмотрим на приведенное выше дерево. Легко заметить, что некоторые входные данные пересчитываются при каждом обращении к ним.

Временная сложность — O(n * log₁₀n).

Что лучше: рекурсия, цикл for или мемоизация?

Нельзя сказать, что какая-то из этих техник однозначно лучше других. Вам просто нужно знать, в каких случаях какая из них будет наиболее подходящей и эффективной. Это, конечно же, зависит от ваших требований.

Итерация с помощью цикла for будет быстрее, чем рекурсия, потому что рекурсия должна иметь дело с фреймом рекурсивного стека вызовов. Однако, если рекурсия написана на языке, который оптимизирует «хвостовой» вызов, это устраняет излишние расходы, и тогда рекурсия сравнима с циклом for .

Наконец, мемоизация лучше, когда нужно иметь дело только с некоторыми более мелкими подзадачами, а не решать их все.

Таким образом, каждый из разобранных нами в этой статье методов по-своему хорош. Стоит помнить о существовании и особенностях каждого из них и выбирать наиболее оптимальный под вашу задачу.

Источник