- Площадь ромба онлайн
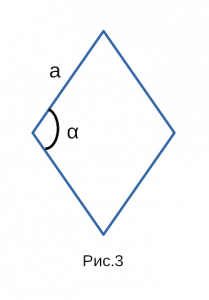
- 1. Площадь ромба через сторону и угол
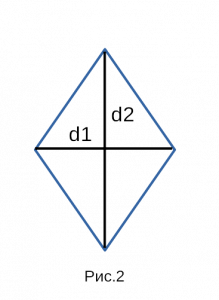
- 2. Площадь ромба через диагонали
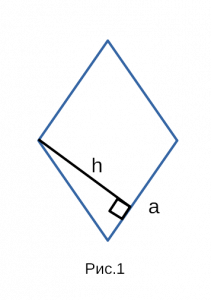
- 3. Площадь ромба через сторону и высоту
- 4. Площадь ромба через угол и противолежащую диагональ
- 5. Площадь ромба через угол и диагональ из данного угла
- 6. Площадь ромба через угол и радиус вписанной в ромб окружности
- 7. Площадь ромба через сторону и радиус вписанной в ромб окружности
- Написать программу для нахождения 25% площади ромба по двум диагоналям
- Функции. Площадь ромба
- Решение
- Площадь ромба через диагонали: онлайн-калькулятор
- Формула площади ромба через диагонали
- Как найти площадь ромба
Площадь ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти площадь ромба по известным элементам. Для нахождения площади ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
1. Площадь ромба через сторону и угол
Пусть задан ромб ABCD (Рис.1). Выведем формулу вычисления площади ромба через сторону и угол.
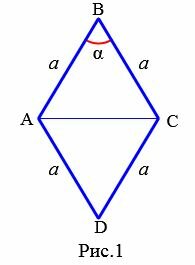 |
Проведем диагональ AC. Тогда ромб делится на два треугольника ABC и ADC. Противолежащие углы ромба равны (свойство 1 статя Ромб). Поэтому треугольники ABC и ADC равны по двум сторонам и углу между ними. Площадь треугольника ABC по двум сторонам и углу между ними вычисляется по формуле:
| \(\small S=AB \cdot BC \cdot \sin \alpha \) |
или, учитывая, что AB=BC=a:
| \(\small S_ |
Аналогично, площадь треугольника ADC вычисляется по формуле
| \(\small S_ |
Поэтому площадь ромба равна:
2. Площадь ромба через диагонали
Пусть известны диагонали d1 и d2 ромба ABCD (Рис.2). Выведем формулу вычисления площади ромба через диагонали.
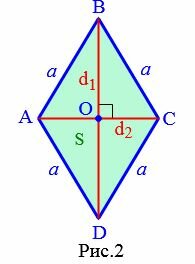 |
Поскольку диагонали ромба перепендикулярны и точкой пересечения делятся пополам (свойства 6 и 5 ромба), то они разделяют ромб на четыре прямоугольных треугольника. Тогда эти прямоугольные треугольники равны по двум катетам: \( \small \frac
| \(\small S_ |
Тогда площадь ромба равна:
3. Площадь ромба через сторону и высоту
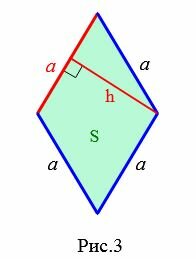 |
Пусть известны сторона a и высота h ромба (Рис.3). Так как ромб является параллелограммом, то площадь ромба вычисляется по формуле площади параллелограмма:
4. Площадь ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащий диагональ d=AC (Рис.4). Выведем формулу вычисления площади ромба.
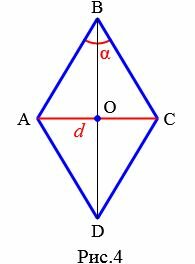 |
Проведем другой диагональ BD. Как было отмечено в параграфе 2, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Найдем площадь одного из них:
| \(\small S_ | (3) |
| \(\small \frac<\large OB > <\large AO>= \mathrm |
| \(\small OB= AO \cdot \mathrm | (4) |
Подставим (4) в (3):
| \(\small S_ |
или, учитывая что \( \small AO=\frac<\large d><\large 2>,\) получим:
| \(\small S_ | (5) |
Тогда площадь ромба равна:
| \(\small S= 4 \cdot S_ | (6) |
5. Площадь ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠BAD ромба и диагональ из данного угла d=AC (Рис.5). Выведем формулу вычисления площади ромба.
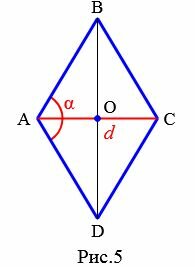 |
Проведем другой диагональ BD. Как было отмечено в параграфе 2, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Найдем площадь одного из них:
| \(\small S_ | (7) |
| \(\small \frac<\large OB > <\large AO>= \mathrm |
| \(\small OB= AO \cdot \mathrm | (8) |
Подставим (8) в (7):
| \(\small S_ |
или, учитывая что \( \small AO=\frac<\large d><\large 2>,\) получим:
| \(\small S_ | (9) |
Тогда площадь ромба равна:
| \(\small S= 4 \cdot S_ | (10) |
6. Площадь ромба через угол и радиус вписанной в ромб окружности
Пусть известны один из углов α=∠ABC ромба и радиус r вписанной в ромб окружности (Рис.6). Выведем формулу вычисления площади ромба.
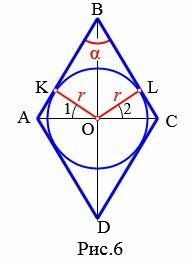 |
Как мы отметили выше, диагонали разделяют ромб на четыре равных прямоугольных треугольника. В частности
Тогда \( \small \angle BAO=\angle BCO=90°-\frac< \large \alpha > <\large 2>\). Треугольники AKO и CLO также прямоугольные. Следовательно
| \( \small \angle 1=90°- \angle BAO \) \( \small =90°- (90°-\frac< \large \alpha ><\large 2>) \) \( \small =\frac< \large \alpha ><\large 2>, \) | (12) |
| \( \small \angle 2=90°- \angle BCO \) \( \small =90°- (90°-\frac< \large \alpha ><\large 2>) \) \( \small =\frac< \large \alpha ><\large 2>. \) | (13) |
Применим теорему синусов для прямоугольного треугольника AOB:
| \( \small \frac<\large AO><\large \sin \frac< \alpha ><2>>= \frac<\large OB><\large \sin \left( 90°-\frac< \alpha > < 2>\right) >\) \( \small =\frac<\large OB><\large \cos \frac< \alpha > < 2>> \) |
Для прямоугольного треугольника AKO имеем:
или, учитывая (12) и KO=r:
Подставляя (15) в (14), получим:
Найдем площадь треугольника AOB:
| \( \small S_ | (17) |
Подставляя (15) и (16) в (17), получим:
| \( \small S_ |
Тогда площадь ромба равна:
7. Площадь ромба через сторону и радиус вписанной в ромб окружности
Пусть известны сторона a=AB ромба и радиус r вписанной в ромб окружности (Рис.7). Найдем площадь ромба.
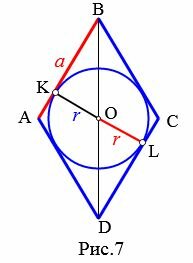 |
Прямая AB является касательной к окружности вписанной в ромб. Тогда \( \small OK ⊥ AB \). Прямая CD является касательной к окружности вписанной в ромб. Тогда \( \small OL ⊥ CD \). Поэтому треугольники BKO и DLO прямоугольные. Эти треугольники равны по гипотенузе и катету (BO=OD, KO=OL). Тогда \( \small \angle BOK=\angle DOL \). Углы BOK и KOD смежные. Следовательно \( \small \angle KOD=180°-\angle BOK. \) \( \small \angle KOD+\angle DOL \) \( \small =180°-\angle BOK+\angle DOL=180°. \) Получили, что отрезки KO и OL находятся на одной прямой. То есть KL=KO+OL=2r. Поскольку \( \small KL ⊥ AB, \) то является высотой ромба. Площадь ромба по стороне и высоте вычисляется из формулы (3). Тогда имеем:
Источник
Написать программу для нахождения 25% площади ромба по двум диагоналям
ВАРИАНТ №19
1. Дана квадратная матрица А порядка N и вектор Х =
2. F(x) = , для x[-1;5], hx = 0,4
3. Написать программу, в которой:
a. запрашивается форма обучения (з/о, очная) студента,
b. сравнивается введенная информация со значением строковой переменной (за-данным в программе),
c. выводится на экран сообщение (совпала или не совпала информация)
4. Написать программу для нахождения 25% площади ромба по двум диагоналям.
5. Написать программу для нахождения значения переменной S по формуле:
S=ln1+ln2+. +ln n
Помогите пожалуйста по вашему профилю(3 4 5 вопросы) если остальные тоже подскажите тоже буду очень рад!
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Написать программу для нахождения 25% площади ромба по двум диагоналям
2. Написать программу для нахождения 25% площади ромба по двум диагоналям.

1)Составить функцию нахождения площади ромба по его диагоналям. С помощью данной функции вычислить.

Составьте программу нахождения площади ромба по его стороной и острым углом ( угол предварительно.

1. Дан файл F, компоненты которого являются действительными числами. Число компонент файла кратно.
Источник
Функции. Площадь ромба
Помощь в написании контрольных, курсовых и дипломных работ здесь.

нужен код программы,заранее спасибо

Даны длина стороны и меньший угол ромба. Найти площадь ромба. Экзамен скоро сдавать, а никак не.

Здравствуйте. Помогите решить две очень простые задачи. 1. Написать программу, вычисляющую.
Решение
Найти площадь ромба
Добрый день! Вызвать функцию через цикл, которая как параметр получает стороны ( — ну ) ромба и.
Определить площадь ромба
Дан ромб ABCD.Окружность радиуса R описана около треугольника ABD и проходит через центр.
найти площадь ромба
Помогите. задание, ввести одну сторону ромба и диагональ

Задан ромб с диагоналями a и b. Определить площадь ромба.
Вычислить площадь и периметр ромба
Ромб описывают длины диагоналей «Д1″и «Д2», периметр «П» и площадь «С». Два числовых значений с.
Источник
Площадь ромба через диагонали: онлайн-калькулятор
Найти площадь фигуры можно несколькими способами. Один из них – использовать в расчетах значения диагоналей. Калькулятор на нашем сайте доступен без регистрации. Пользователь может вводить значения без ограничений в количестве вычислений.
Сервис используют учащиеся школ и университетов, родители учеников, преподаватели. Также среди пользователей работники технических профессий, которым необходимо быстро произвести расчеты.
- Введите значения диагоналей ромба в соответствующие окна.
- Выберите единицы измерения, в которых представлены значения диагоналей. Также установите единицу измерения, в которой необходимо получить ответ. Отправьте задание на расчет кнопкой «Найти».
- Получайте подробное решение и ответ.
Формула площади ромба через диагонали
В автоматическом подсчете сначала единицы измерения переводятся в необходимые. Затем программа переходит к непосредственному решению.
Чтобы вычислить площадь ромба по диагоналям, следует произведение диагоналей разделить пополам:
S = 1 2 · d 1 · d 2 .
Сервис с калькуляторами создан для расширения возможностей получить качественное образование. Zaochnik позволяет:
- Сэкономить деньги на репетиторах. В разделе собраны все основные темы. С их помощью ученик может самостоятельно подготовиться к поступлению в ВУЗ.
- Не отставать от программы. Пропущенная тема легко отрабатывается на примерах. Пошаговое решение помогает запомнить алгоритм и применять его в дальнейшем.
- Быстро проверять выполненные задания. Родители и преподаватели теперь смогут тратить меньше времени на проверку домашних заданий.
- Не растеряться на контрольной. Если необходимо срочно вспомнить формулу и свериться с ответом, найдите нужный калькулятор, введите данные и получите вычисления с готовым ответом.
Если тема все равно осталась непонятной или срочно надо сделать объемное задание, напишите консультанту. Он подберет опытного преподавателя из нашего штата. По выгодной цене вы получите готовый к сдаче проект.
Источник
Как найти площадь ромба
Площадь ромба можно вычислить разными способами.
Например, через половину произведения двух диагоналей
друг на друга, через синус и сторону в квадрате…
Также, площадь ромба равна площади параллелограмма.
Как следствие, так, как ромб является параллелограммом, с
равными сторонами, поэтому площадь ромба
можно найти через площадь параллелограмма.
Для ромба истинны и верны все свойства параллелограмма.
Формула площади ромба и формула
площади параллелограмма одинаковая.
Ромб — параллелограмм, у которого
все четыре стороны равны.
Формулировка площади ромба через параллелограмм:
Формула площади ромба через параллелограмм:
a — основание; h — высота;
Площадь ромба, можно также найти другим способом. Для
этого мысленно разделим ромба на четыре треугольника,
так чтобы каждая вершина была соединена с противоположной
вершиной. Получившиеся линии называют диагоналями. Если
известны длины двух диагоналей ромба, то можно найти площадь.
Формула площади ромба через две диагонали:
\( S = \frac<1>2d_1 d_2 \)
d1 и d2 — диагонали;
В самых редких случаях, если известен синус и одна из сторон,
используют формулу площади ромба через синус и квадрат стороны.
Формулировка площади ромба через синус и сторону в квадрате:
Формула площади ромба через синус и сторону в квадрате:
a — сторона; sin α — синус угла;
Рис. 1 — площадь ромба через площадь параллелограмма / основание и высоту.
Рис. 2 — площадь ромба через две диагонали
Рис. 3 — площадь ромба через синус и сторону в квадрате
Также, вы можете прочитать про свойства и признаки ромба.
Источник