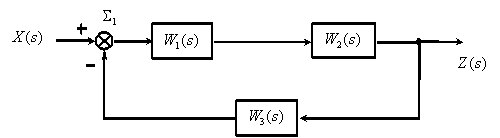
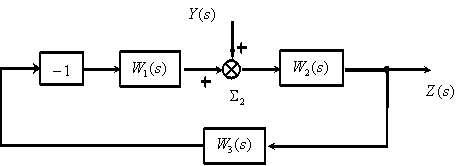
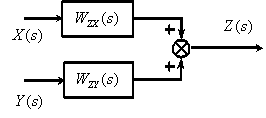
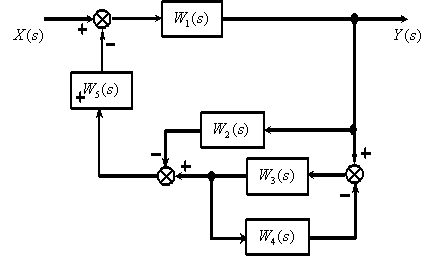
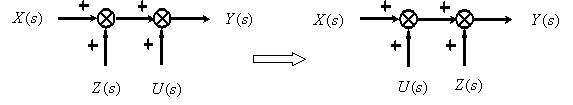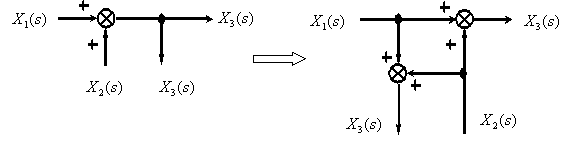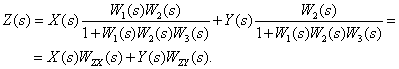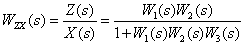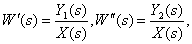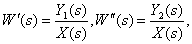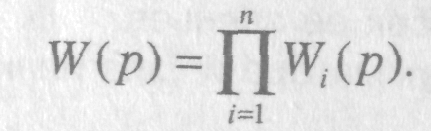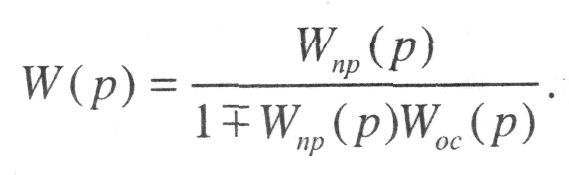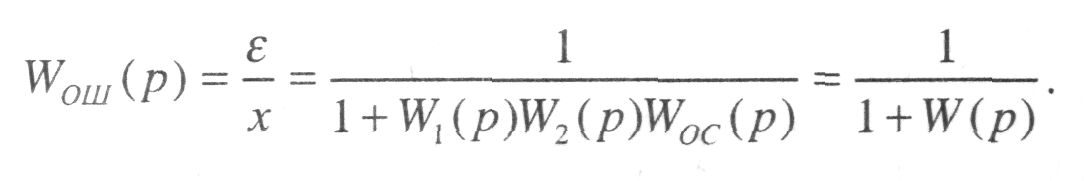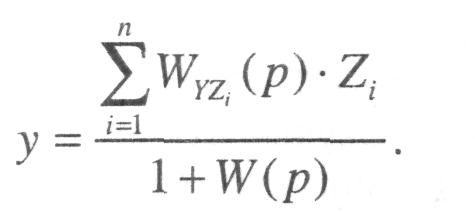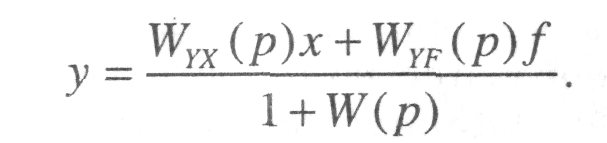Вывести передаточную функцию для заданной структурной схемы
Правила эквивалентных преобразований структурных схем систем автоматического управления
Выше были рассмотрены математические модели отдельных динамических звеньев. САУ представляет собой систему, состоящую из функциональных элементов, каждый из которых может быть представлен в виде динамического звена. То есть САУ можно представить в виде совокупности динамических звеньев с известными математическими моделями. Рассмотрим структуру типичной САУ
где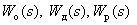 
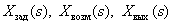
передаточные функции соответственно объекта, датчика и регулятора, 
изображения задающего, возмущающего и выходного сигналов.
В процессе анализа и синтеза САУ необходимо получать передаточные функции САУ, которые связывают выходную переменную с заданием и возмущением в САУ, по известным структурной схеме и передаточным функциям динамических звеньев, входящих в состав САУ.
Аналогичная задача возникает в том случае, когда известны частотные характеристики динамических звеньев, а необходимо определить частотные характеристики САУ, характеризующие связи между выходом и входом САУ.
Решением этих задач мы и займемся в дальнейшем.
Эта задача решается путем преобразования (сворачивания) структурной схемы к одному динамическому звену с искомой передаточной функцией на основе использования правил эквивалентных преобразований структурных схем и принципа суперпозиции (наложения).
Правила эквивалентных преобразований позволяют найти необходимую передаточную функцию САУ, свернув структурную схему к одному динамическому звену с искомой передаточной функцией.
Рассмотрим правила эквивалентных преобразований, не изменяющих свойств систем и необходимых для нахождения передаточной функции:
Последовательное соединение динамических звеньев.
Параллельное соединение динамических звеньев.
Замкнутый контур с отрицательной обратной связью.
Замкнутый контур с положительной обратной связью.
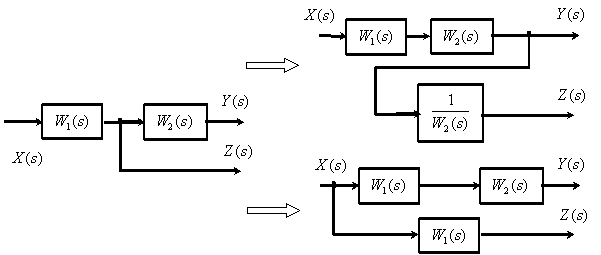
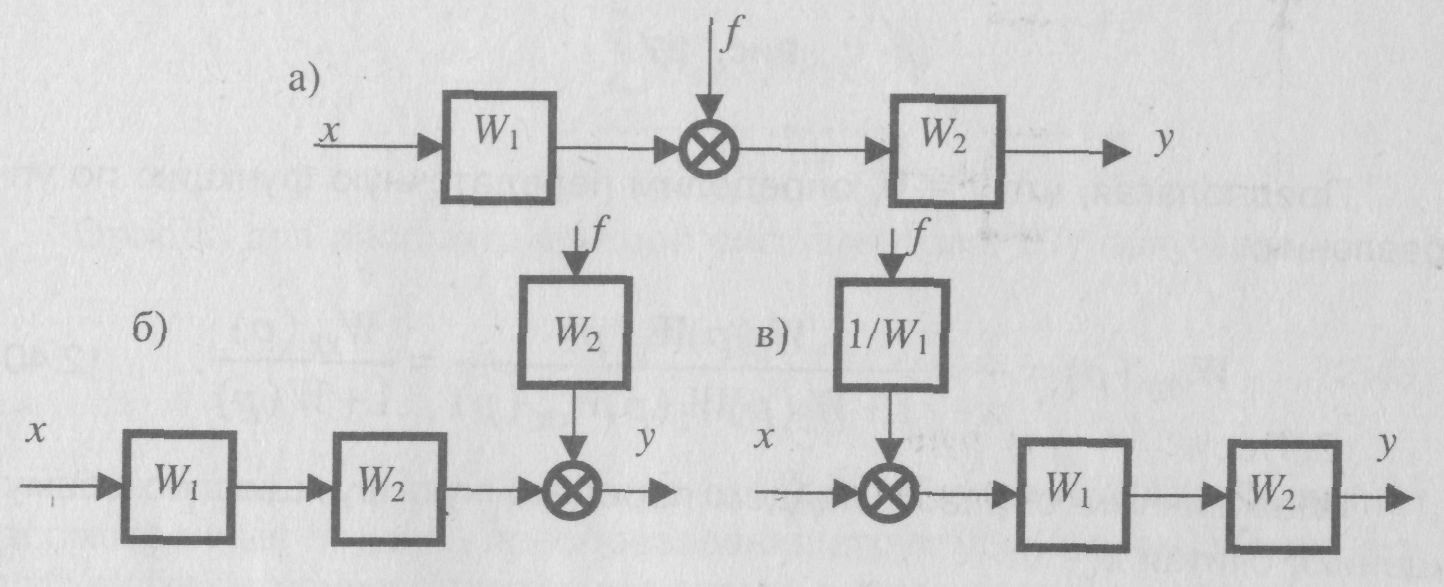
Перенос точки ветвления через динамическое звено.
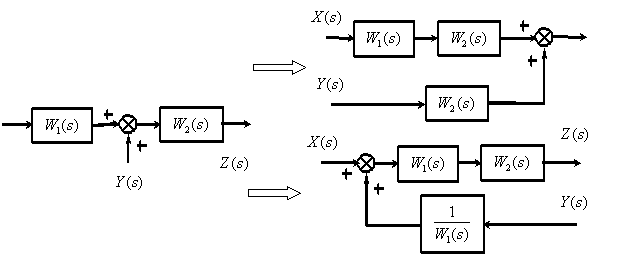
Перенос суммирующего звена через динамическое звено.
Перестановка суммирующих звеньев.
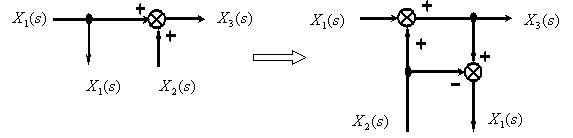
Перенос точки ветвления с выхода на вход суммирующего звена.
Перенос точки ветвления с входа на выход суммирующего звена.
Принцип суперпозиции (наложения)
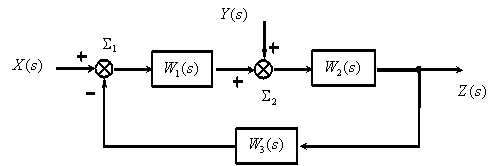
Применим рассмотренные правила для упрощения структурной схемы
Процесс преобразования, который часто называют свертыванием структурной схемы, выглядит следующим образом.
Перенесем суммирующее звено 
через динамическое звено 
.
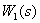
Поменяем местами суммирующие звенья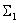 
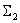
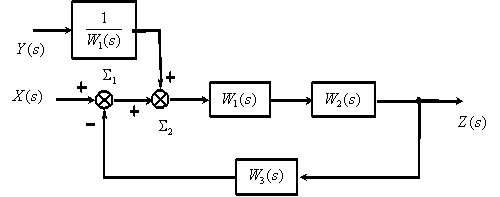
и
.
Преобразуем последовательно включенные динамические звенья 
и 
.
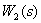
Преобразуем замкнутый контур с отрицательной обратной связью (
).
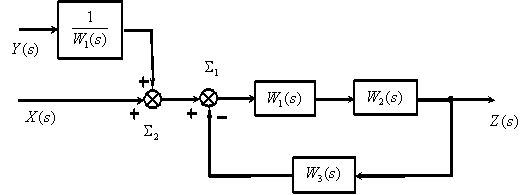
Перенесем суммирующее звено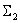 
вправо.
Преобразуем последовательно включенные звенья..
В соответствии с полученной структурной схемой запишем операторное уравнение
Уравнение показывает, что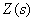 
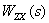
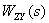
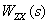
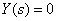
является линейной комбинацией изображений входных сигналов, взятых с коэффициентами 
и 
. Выясним смысл этих коэффициентов на примере коэффициента 
. Для этого положим в (1) 
, тогда получим
Таким образом, из (2) следует, 
это передаточная функция динамического звена, к которому свернута структурная схема в предположении, что изображения всех входных сигналов, кроме 
, равны нулю.
Теперь становится ясным смысл и самого операторного уравнения (1), описывающего систему. Он заключается в том, что реакция линейной системы на совместно действующие входные сигналы может быть определена в виде суммы частичных реакций, каждая из которых вычисляется в предположении, что на систему действует только один входной сигнал, а остальные равны нулю.
По сути это формулировка фундаментального принципа, который называют принципом наложения или суперпозиции. Этот принцип можно рассматривать как дополнение к правилам эквивалентных преобразований структурных схем и активно использовать на практике.
Практически принцип суперпозиции для нахождения конкретной передаточной функции используют следующим образом. Полагают равными нулю все входные сигналы, кроме необходимого сигнала, а затем выполняют преобразование структурной схемы в одно динамическое звено.
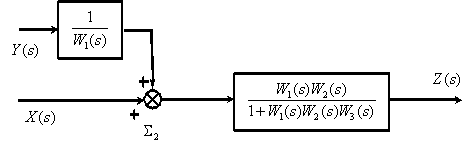
Рассмотрим использование принципа суперпозиции на примере показанной на рис. 1 структурной схемы.
Полагаем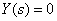 
и изобразим соответствующую этому случаю структурную схему.
Используя эквивалентные преобразования, получим
.
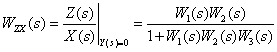
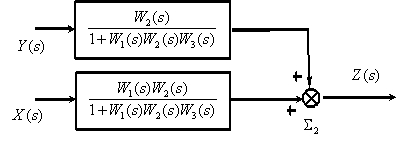
Полагаем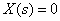 
и изобразим соответствующую этому случаю структурную схему.
Используя эквивалентные преобразования, получим
.
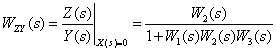
Имея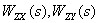 
, в соответствии с принципом суперпозиции получим «свернутую» структурную схему САУ.
Контрольные вопросы и задачи
Какие задачи позволяют решать правила эквивалентных преобразований структурных схем?
Дайте определение принципа суперпозиции применительно к структурным схемам систем автоматического управления.
Как используют принцип суперпозиции на практике?
Определите передаточные функции
по следующей структурной схеме
.
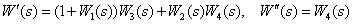
Определите передаточную функцию, эквивалентную структурной схеме.
.
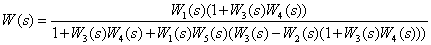
Определите передаточные функции
по следующей структурной схеме
.
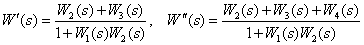
Источник
Преобразование структурных схем
Преобразование структурных схем
Структурной схемой в теории автоматического управления называется представление САР в виде совокупности динамических звеньев. В прямоугольных блоках записываются передаточные функции элементарных динамических звеньев системы. Стрелками обозначаются связи между элементами, а также воздействия: выходное – у, задающее – х, возмущающее – f и т.п.
Узлы (разветвления сигналов) обозначаются точками на стрелках, а сумматоры сигналов обозначаются в виде кружка. Например, первый сумматор вычисляет сигнал рассогласования (ошибки): ε = x – z.
На рис. 1 приведена структурная схема системы автоматического управления.
Рис. 1. Структурная схема САР
Структурная схема представляет собой математическую модель САР, состоящую из совокупности типовых динамических звеньев, и является очень удобным, информативным и наглядным способом представления системы. Для анализа и синтеза САУ необходимо знать математическое описание системы в виде ее общей передаточной функции. Структурные схемы позволяют достаточно просто решить эту проблему путем сворачивания всей совокупности типовых динамических звеньев в одно динамическое звено. Для этого применяются три правила преобразования структурных схем и правила переноса узла и сумматора.
Звенья в структурных схемах могут соединяться между собой последовательно, параллельно и встречно (по схеме с обратной связью) (рис. 2).
Рис. 2. Виды соединений звеньев
1. Передаточная функция цепочки последовательно соединенных звеньев (рис. 2,а) равна произведению их передаточных функций
2. Передаточная функция группы параллельно соединенных звеньев (рис. 2,б) равна их сумме передаточных функций
3. Передаточная функция группы звенев, соединенных по схеме с обратной связью (рис. 2,в), определяется как отношение передаточной функции прямой цепи к выражению – единица минус (для положительной обратной связи) или плюс (для отрицательной обратной связи) – передаточная функция разомкнутой цепи:
Такая передаточная функция называется передаточной функцией замкнутой системы (замкнутой цепи). Т.е. при положительной обратной связи сигнал обратной связи прибавляется к задающему воздействию, а при отрицательной – вычитается из него. Прямой цепью называется совокупность звеньев, передающая сигнал от входа к выходу. Передаточная функция замкнутой цепи (системы) состоит из передаточной функции прямой цепи и передаточной функции обратной связи. Передаточная функция разомкнутой цепи в случае одноконтурной САУ представляет собой произведение передаточных функций всех ее звеньев.
Правила переноса сумматора и узла иллюстрируются на рис. 3 и рис. 4 соответственно. Вариантам а) на этих рисунках соответствуют исходные схемы, а вариантам б) и в) – преобразованные.
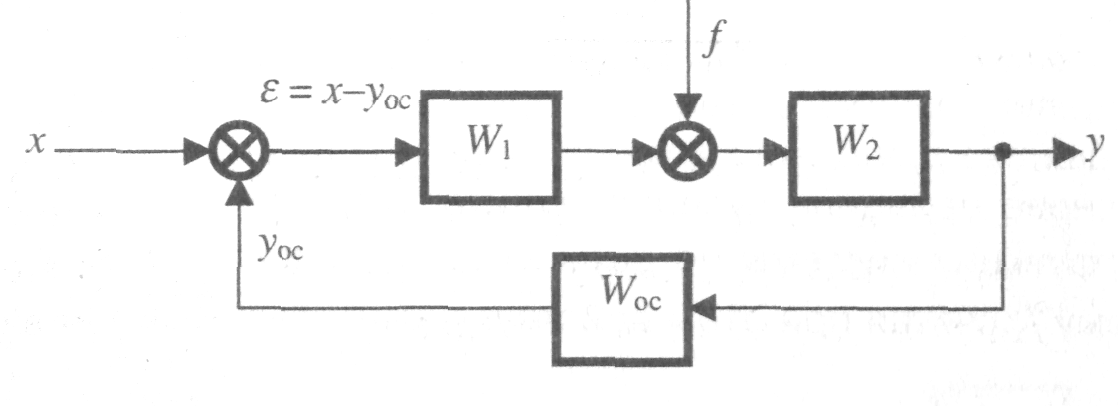
Определим передаточные функции по управлению, по возмущению и по ошибке для одноконтурной линейной САУ (рис. 5).
На основе принципа суперпозиции определим поочередно передаточные функции системы по двум входам – управляющему х и возмущающему f считая при этом действующим только один из входов. Предполагая, что
f = 0, определим передаточную функцию по управлению
Аналогичным образом найдем передаточную функцию по возмущению, считая х = 0:
Передаточную функцию по ошибке ε получим после преобразования исходной структурной схемы САУ в вид, представленный на рис. 6 (f = 0, х = 0).
Рис. 6
Передаточная функция прямой цепи между входным воздействием и сигналом ошибки равна 1, тогда передаточная САУ по ошибке определится в виде
Анализируя передаточные функции WУПР (p), WВОЗ (p) и WОШ (p) для случая, когда на линейную систему одновременно подается несколько воздействий zi, на основе принципа суперпозиции можно определить следующую зависимость выходного сигнала от совокупности входных
Отсюда для рассматриваемой системы (рис. 5) получаем
Эти уравнения используются при исследовании САУ. Применяя рассмотренные правила преобразования структурных схем, можно любую многоконтурную структурную схему, в том числе и с перекрещивающимися контурами, привести к одноконтурному виду и затем свернуть в одно динамическое звено, передаточная функция которого будет являться передаточной функцией исходной многоконтурной системы.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
