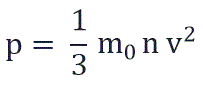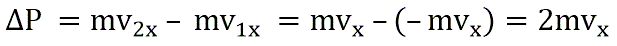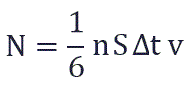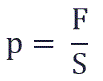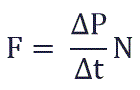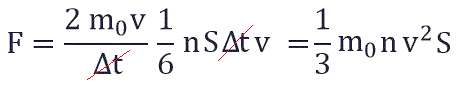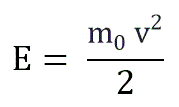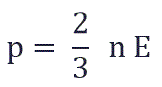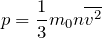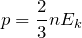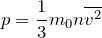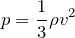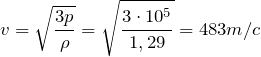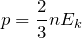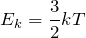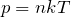- Основное уравнение молекулярно-кинетической теории (МКТ) с выводом
- Основное уравнение молекулярно-кинетической теории
- Вывод основного уравнения МКТ
- Вывести основного уравнения мкт
- Вывести основного уравнения мкт
- Основное уравнение МКТ
- Основное уравнение МКТ
- Определение и формула уравнения МКТ
- Основное уравнение МКТ для модели идеального газа
- Примеры решения задач
Основное уравнение молекулярно-кинетической теории (МКТ) с выводом
В статье рассмотрена модель идеального газа, приведено основное уравнение молекулярно-кинетической теории и его вывод.
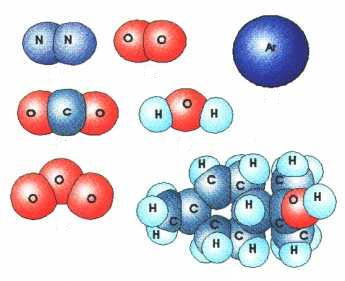
Чтобы объяснить свойства материи в газообразном состоянии, в физике применяется модель идеального газа. Идеальный газ — разреженный, состоящий из одного типа атомов газ, частицы которого не взаимодействуют между собой. Помимо основных положений МКТ эта модель предполагает, что:
- молекулы имеют пренебрежимо малый объем в сравнении с объемом емкости
- при сближении частиц друг с другом и с границами емкости имеют место силы отталкивания
Основное уравнение молекулярно-кинетической теории
Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа — это совокупность всех ударов молекул о стенки сосуда. Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:
p – давление молекул газа на границы емкости,
m0 – масса одной молекулы,
n — концентрация молекул, число частиц N в единице объема V;
v 2 — средне квадратичная скорость молекул.
Вывод основного уравнения МКТ
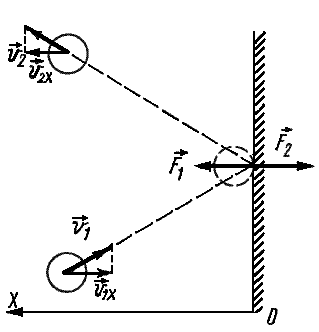
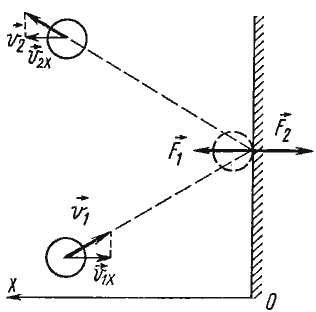
Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция vx скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:
Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv1x = –mvx на mv2x = mvx.
Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:
Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6. Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:
S – площадь этой стенки
n — концентрация частиц
Давление p равно отношению силы F к площади S, на которую действует эта сила:
Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:
Исходя из вышенаписанного получаем:
Если заменить среднее значение кинетической энергии поступательного движения молекул — E:
и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:
Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.

Понравилась статья, расскажите о ней друзьям:
Источник
Вывести основного уравнения мкт
9.1. Модель идеального газа в молекулярно-кинетической теории
Законы идеальных газов, найденные опытным путём, находят довольно простое объяснение в молекулярно-кинетической теории (МКТ). Она исходит при этом из упрощённых представлений о строении газа. Это обусловлено рядом причин, в частности, неточным знанием сил взаимодействия между молекулами. Однако, как оказывается, даже такая упрощённая модель газа позволяет найти уравнение состояния, правильно описывающее его поведение.
В молекулярно-кинетической теории принимается следующая идеализированная модель газа – идеальный газ. Молекулы газа считаются твёрдыми, абсолютно упругими шариками, причём размеры молекул малы по сравнению со средним расстоянием между ними. Это означает, что собственный суммарный объём молекул значительно меньше объёма сосуда, в котором находится газ. Взаимодействие между молекулами проявляется только при непосредственном столкновении их друг с другом. Между столкновениями молекулы движутся по инерции. Движение молекул подчиняется законам механики Ньютона.
Для нахождения уравнения состояния газа необходимо сделать ещё важное упрощающее предположение, а именно, считать движение любой молекулы газа беспорядочным, хаотичным.
Аккуратный вывод основного уравнения молекулярно-кинетической теории идеального газа требует принимать во внимание ряд моментов, например, наличие в газе молекул, движущихся с разными по величине скоростями, столкновения молекул между собой, характер столкновения отдельной молекулы со стенкой сосуда (упругий или неупругий). В разделе 7.3 будет рассмотрен упрощённый вариант вывода основного уравнения молекулярно-кинетической теории.
9.2. Давление идеального газа
Давление, которое оказывает газ на стенку сосуда, есть результат ударов молекул газа о стенку. Если бы в сосуде содержалось всего несколько молекул, то их удары следовали бы друг за другом редко и беспорядочно. Поэтому нельзя было бы говорить ни о какой регулярной силе давления, действующей на стенку. Стенка подвергалась бы отдельным практически мгновенным бесконечно малым толчкам. Если же число молекул в сосуде очень велико, то велико и число ударов их о стенку сосуда. Одновременно о стенку сосуда ударяется громадное количество молекул. Очень слабые силы отдельных ударов складываются при этом в значительную по величине и почти постоянную силу, действующую на стенку. Среднее по времени значение этой силы, отнесённое к единичной площадке, и есть давление газа, с которым имеет дело термодинамика.
Пусть в сосуде объёма $$ V$$ находятся $$ N$$ одинаковых молекул идеального газа, а $$
Источник
Вывести основного уравнения мкт
161 дн. с момента
до конца учебного года
Основное уравнение МКТ
Слово «газ» в переводе с греческого звучит как «хаос». Это отлично характеризует движение частичек, которое на самом деле беспорядочно и хаотично. Газ не образует определенной поверхности, он заполняет весь доступный ему объем. Такое состояние веществ — самое распространенное в нашей Вселенной.
Законы, которые определяют свойства и поведение такого вещества, легче всего формулировать и рассматривать на примере состояния, в котором относительная плотность молекул и атомов низкая. Оно получило название «идеальный газ». В нем расстояние между частицами больше, чем радиус взаимодействия межмолекулярных сил.
Итак, идеальный газ — это теоретическая модель вещества, в которой почти полностью отсутствует взаимодействие частиц.
Как показывает опыт, молекулы газа распределяются по всему предоставленному для него объему. Следовательно, главную роль в поведении газа играет хаотическое движение молекул, а силы взаимодействия малы, и ими можно пренебречь. Это означает, что молекула газа движется равномерно и прямолинейно, пока не столкнется с другой молекулой. При столкновении изменяется величина и направление скорости движения молекулы, и она снова движется равномерно и прямолинейно до следующего столкновения. Дли на свободного пробега (расстояние между двумя последовательными столкновениями молекулы) λ
10 -7 м. При такой длине свободного пробега только 0,04 % пространства, занятого газом, приходится на собственный объем его молекул. Это дает право воспользоваться моделью идеального газа.
Идеальный газ — это газ с достаточно простыми свойствами:
- Между частицами идеального газа нет сил взаимодействия; они действуют только при столкновениях частиц (т.е. потенциальная энергия взаимодействия частиц идеального газа настолько мала, что ею пренебрегают по сравнению с кинетической энергией);
- Частицы в идеальном газе имеют настолько маленькие размеры, что их можно считать материальными точками. Их суммарный объём ничтожно мал по сравнению с объёмом сосуда, в котором находится газ. И этим объёмом пренебрегают;
- От столкновения до столкновения частицы движутся равномерно и прямолинейно;
- Движение частиц идеального газа подчиняется законам Ньютона;
- Частицы идеального газа ведут себя при столкновениях как абсолютно упругие шарики;
- Среднее время между столкновениями частиц намного превышает время их взаимодействия при соударении. Поэтому временем взаимодействия пренебрегают также.
При небольших давлениях и не очень низких температурах реальные газы близки к идеальному газу. При высоких давлениях молекулы газа находятся так близко, что между ними возникают заметные силы взаимодействия. Пренебречь их собственным объемом нельзя, и газ уже не является идеальным.
Реальные газы при комнатной температуре и нормальном давлении ведут себя как идеальные газы. Идеальными газами можно считать такие газы как гелий, водород, свойства которых уже при обычных условиях отвечают закономерностям идеального газа.
Для описания свойств газов можно пользоваться:
- микроскопическими параметрами (скорость, масса молекулы, ее энергия и др.), которые являются характеристиками молекул и средние численные значения которых находятся только расчетным путем;
- макроскопическими параметрами (давление, температура, объем газа), значение которых определяется совместным действием огромного числа молекул. Макропараметры — это параметры, характеризующие состояние системы (газа) в целом и не имеющие смысла в применении к отдельным частицам системы. Численные значения их находят измерением с помощью приборов и расчетным путем.
Давление газа p — это средняя сила ударов его молекул о тело (например, о стенки сосуда), отнесенная к единице поверхности тела.
Абсолютная температура T — мера средней кинетической энергии теплового движения молекулы (см. Температура и тепловое равновесие системы).
Под объемом газа V понимают внутренний объем сосуда, в котором находится газ.
P =1/3 monV 2 — основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его частиц о стенки сосуда.
Источник
Основное уравнение МКТ
Определение и формула уравнения МКТ
Здесь 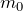
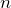
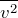
Основное уравнение МКТ наглядно объясняет, каким образом идеальный газ создает давление на окружающие его стенки сосуда. Молекулы все время ударяются о стенку, воздействуя на нее с некоторой силой F. Тут следует вспомнить третий закон Ньютона: когда молекула ударяется о предмет, на нее действует сила -F, вследствие чего молекула «отбивается» от стенки. При этом мы считаем соударения молекул со стенкой абсолютно упругими: механическая энергия молекул и стенки полностью сохраняется, не переходя во внутреннюю энергию тел. Это значит, что при соударениях изменяются только скорости молекул, а нагревания молекул и стенки не происходит.
Зная, что соударение со стенкой было упругим, мы можем предсказать, как изменится скорость молекулы после столкновения. Модуль скорости останется таким же, как и до соударения, а направление движения изменится на противоположное относительно оси Ох (считаем, что Ох – это та ось, которая перпендикулярна стенке).
Молекул газа очень много, движутся они хаотично и о стенку ударяются часто. Найдя геометрическую сумму сил, с которой каждая молекула воздействует на стенку, мы узнаём силу давления газа. Чтобы усреднить скорости молекул, необходимо использовать статистические методы. Именно поэтому в основном уравнении МКТ используют усредненный квадрат скорости молекул 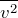
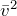
Теперь ясен физический смысл уравнения: чем больше молекул содержится в объеме, чем они тяжелее и чем быстрее движутся – тем большее давление они создают на стенки сосуда.
Основное уравнение МКТ для модели идеального газа
Следует заметить, что основное уравнение МКТ выводилось для модели идеального газа с соответствующими допущениями:
- Соударения молекул с окружающими объектами абсолютно упругие. Для реальных же газов это не совсем так; часть кинетической энергии молекул всё-таки переходит во внутреннюю энергию молекул и стенки.
- Силами взаимодействия между молекулами можно пренебречь. Если же реальный газ находится при высоком давлении и сравнительно низкой температуре, эти силы становятся весьма существенными.
- Молекулы считаем материальными точками, пренебрегая их размером. Однако размеры молекул реальных газов влияют на расстояние между самими молекулами и стенкой.
- И, наконец, основное уравнение МКТ рассматривает однородный газ – а в действительности мы часто имеем дело со смесями газов. Как, например, воздух.
Однако для разреженных газов это уравнение дает очень точные результаты. Кроме того, многие реальные газы в условиях комнатной температуры и при давлении, близком к атмосферному, весьма напоминают по свойствам идеальный газ.
Как известно из законов динамики, кинетическая энергия любого тела или частицы 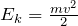
Также кинетическая энергия газовых молекул выражается формулой 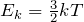
Основное уравнение МКТ лежит в основе термодинамики. Также оно используется на практике в космонавтике, криогенике и нейтронной физике.
Примеры решения задач
| Задание | Определить скорость движения частиц воздуха в нормальных условиях. |
| Решение | Используем основное уравнение МКТ, считая воздух однородным газом. Так как воздух на самом деле – это смесь газов, то и решение задачи не будет абсолютно точным. |
Можем заметить, что произведение 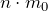
Тогда предыдущее уравнение примет вид:
В нормальных условиях давление равно 10 5 Па, плотность воздуха 1,29кг/м 3 – эти данные можно взять из справочной литературы.
Из предыдущего выражения получим скорость молекул воздуха:
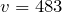 м/с
м/с| Задание | Определить концентрацию молекул однородного газа при температуре 300 К и давлении 1 МПа. Газ считать идеальным. |
| Решение | Решение задачи начнём с основного уравнения МКТ: 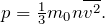 Кинетическая энергия молекул, как и любых материальных частичек: Кинетическая энергия молекул, как и любых материальных частичек: 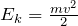 . Тогда наша расчетная формула примет несколько другой вид: . Тогда наша расчетная формула примет несколько другой вид: |
Однако кинетическая энергия молекул в термодинамике определяется и с помощью другого выражения, и напрямую связана с температурой газа:
Подставив эту формулу в предыдущее выражение, получим еще одну форму записи основного уравнения МКТ:
Выразим и рассчитаем концентрацию молекул газа:
Источник