4.3 Основное энергетическое уравнение турбины.
4.3.1 Основное уравнение турбин.
Для определения силовых и энергетических показателей потока в рабочем колесе применим закон момента количества движения в форме, которую уже использовали для определения условия свободного движения жидкости – закона постоянства момента скорости.
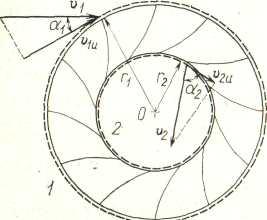
Рассмотрим нормальное сечение рабочего колеса РО турбины (рисунок 4.10), и выделим контрольными поверхностями 1 и 2 область, включающую лопасти рабочего колеса.
Для установившегося осредненного потока внутри выделенной области (межлопастное пространство РК), момент скорости vur не изменяется во времени и, следовательно, d(vur) равно разности:
на контрольных поверхностях 1 и 2.
Рисунок 4.10. Скорости на входной и выходной
кромках лопастей рабочего колеса
Протекающая через рабочее колесо за время dt масса жидкости
В этих условиях закон момента количества движения представляется формулой:
Сумма моментов внешних сил относительно оси вращения ∑MО, действующих на выделенный объем жидкости, определяется следующим образом:
Момент от сил давления на поверхности вращения 1 и 2 и поверхности ободов равен нулю.
Силы веса также не дают момента, так как центр их приложения совпадает с осью.
Остаются силы трения по ограничивающим поверхностям этого объема и силы давления и трения жидкости на лопастях.
В последнем случае обе группы сил дают момент относительно оси, но первую из-за малости можно не учитывать, и тогда остается момент, воздействующий на жидкость со стороны лопастей рабочего колеса М. Искомый же момент рабочего колеса, создаваемый жидкостью на лопастях, будет равен — М.
Далее используя выражения средней циркуляции:
можно выразить момент рабочего колеса через разность средних циркуляции на входе и выходе:
Последняя формула особенно наглядна. Она показывает, что на рабочем колесе создается крутящий момент только в том случае, когда оно воздействием своих лопастей изменяет циркуляцию потока.
Знак Г принимается положительным, если vu совпадает с направлением окружной скорости u. Зная момент и задавая угловую скорость рабочего колеса, можно определить развиваемую им мощность:
Здесь: М – в Н•м, ω – в 1/с, Npк – в Вт. В то же время известно, что мощность турбины выражается формулой Npк = ρgQHη. Это позволяет составить равенство:
или с учетом циркуляции:
Данные формулы представляют собой основное уравнение турбин, или уравнение Л. Эйлера. Левая часть HηГ — энергия в Дж, полученная рабочим колесом от жидкости весом в 1 Н, прошедшей через лопастную систему рабочего колеса. Правая часть содержит кинематические параметры потока при входе на рабочее колесо и после выхода из него.
Таким образом, основное уравнение дает связь между энергетическими и кинематическими параметрами в турбине.
Из последнего уравнения Эйлера можно сделать важные выводы:
1.Выше отмечалось, что наиболее благоприятный по КПД режим работы близок к условиям нормального выхода, когда циркуляция Г2 = 0 или мала. При этом, Г1 = ГО – циркуляции, создаваемые направляющим аппаратом. Отсюда можно определить требуемое значение ГО в зависимости от Н и ω.
2. В процессе прохождения воды через рабочее колесо турбины циркуляция потока должна убывать. Следовательно, рабочее колесо «срабатывает» циркуляцию, созданную направляющим аппаратом.
Источник
Лекция 5 ГМ. Лекция 2 Основное уравнение преобразования энергии в турбине. 2 Кинематика потока в проточной части. 1 Безударный вход потока на рабочее колесо
| Название | Лекция 2 Основное уравнение преобразования энергии в турбине. 2 Кинематика потока в проточной части. 1 Безударный вход потока на рабочее колесо |
| Анкор | Лекция 5 ГМ.doc |
| Дата | 27.08.2018 |
| Размер | 177 Kb. |
| Формат файла |  |
| Имя файла | Лекция 5 ГМ.doc |
| Тип | Лекция #23663 |
| Подборка по базе: Обзорна лекция.doc, 05.10.2021 лекция 7.pdf, Русецкий Игорь Станиславович_Видео лекция № 3 Булева алгебра. Ло, 5 лекция.docx, Хуриев лекция 1 (1).docx, 1 лекция.docx, ИТвПД Лекция 7.docx, Экология.1 лекция..pdf, 1 Лекция безопасность ПП каз.docx, 2,7 лекция.ppt Основное уравнение преобразования энергии в турбине. 4.2 Кинематика потока в проточной части. 4.2.1 Безударный вход потока на рабочее колесо. При ударном входе воды могут иметь место значительные потери энергии. Поэтому стремятся создать условия безударного входа для режима, при котором чаще всего будет эксплуатироваться турбина. Такой режим называется нормальным, или расчетным. Безударным входом, называется такой вход, при котором вектор абсолютной скорости потока на входной кромке лопастей рабочего колеса равен по величине и направлению вектору абсолютной скорости, созданной направляющим аппаратом непосредственно перед входом на лопасти колеса, а относительные скорости направлены по касательной к входному элементу лопасти. Условия безударного входа представлены следующим образом: Обеспечить безударный вход при всех рабочих режимах невозможно. При изменении расхода воды, протекающей через турбину (рисунок 4.7), вектор абсолютной скорости потока Vна входе в колесо будет менять свою величину и направление, так как величина переносной скорости U остается постоянной, а относительная скорость W1 не меняя направления, изменяет свою величину в зависимости от расхода.
Векторные диаграммы для нормального режима при безударном 1. Предположим, что открытие лопаток направляющего аппарата осталось прежним, а рабочий напор увеличился*. Тогда абсолютная скорость на подходе к лопастям колеса, сохраняя направление V0, увеличится до V ‘ 0 (рис. 4.8, а); относительная скорость W‘0 определится как разность векторов V ‘ 0 и U1. Новая относительная скорость W‘0 по направлению не будет совпадать с W1 что и характеризует появление удара, приводящего к завихрениям на входной кромке лопасти и, следовательно, к увеличению потерь энергии. Рисунок 4.8. Треугольники скоростей на входе в рабочее колесо: а) – при нормальном режиме и режиме с увеличенным напором Н, а0=const; б) – при нормальном режиме и режиме с увеличенным открытием а0, Н =const. hуд = 2. При увеличении открытия лопаток направляющего аппарата при неизменном напоре (рис. 4.8, б) увеличивается расход воды и происходит поворот вектора V0 в положение V ‘ 0, а вектора V1 в положение V ‘ 1. Здесь имеет место одинаково направленный поворот векторов абсолютных скоростей до и на входной кромке лопастей. Вследствие этого значительно уменьшается удар при входе на лопасти рабочего колеса, а следовательно, уменьшаются потери энергии, связанные с ним. У радиально-осевых и пропеллерных турбин безударный вход может быть обеспечен только при одном нормальном режиме, а у поворотно-лопастных турбин по одному режиму при каждом угле установки лопастей рабочего колеса, т. е. безударные режимы представляют собой линию нормальных режимов. 4.2.2 Нормальный выход потока с рабочего колеса. Нормальный выход. Нормальным выходом называется такой, при котором абсолютная скорость V2 на выходе с лопастей рабочего колеса перпендикулярна переносной скорости U2, т. е. ά2 = 90° и при этом vU2 = 0 (рисунок 4.7 б). Считалось, что нормальный выход желательно иметь всегда и обосновывалось это тем, что при нормальном выходе будут меньше абсолютные скорости течения воды в отсасывающей трубе и на выходе из нее, вследствие чего ожидалось уменьшение потерь энергии как внутри трубы, так и при выходе из нее. Кроме того, считалось, что при нормальном выходе вследствие отсутствия закрутки потока в отсасывающей трубе будет более равномерное распределение скоростей по сечениям трубы, что должно привести к улучшению кавитационных свойств турбины. Однако эксперименты, проведенные в лабораториях, не подтвердили, казалось бы, на первый взгляд бесспорного предположения. Наоборот, опытами было установлено, что положительная закрутка потока (vU2 совпадает с направлением U2) на выходе из лопастей рабочего колеса соответствующая значению vU2 = 0,2gH, оказывает благоприятное влияние на к. п. д. турбины и ее кавитационные качества. Объясняется это тем, что при закрученном потоке на выходе из рабочего колеса лучше обтекается диффузорная часть отсасывающей трубы и меньше потери в самом рабочем колесе, так как при этом меньше относительные скорости течения воды по лопастям рабочего колеса. В настоящее время не только не избегают ненормального выхода воды с лопастей рабочего колеса, а наоборот, часто при расчете колеса его предусматривают. Рассмотрим, при каких условиях будет нормальный выход. Из треугольника скоростей на выходе (рисунок 4.7 б) имеем: В частности, для осевого потока в сечении непосредственно после рабочего колеса приближенно можно принять: где F2 — площадь поперечного сечения камеры рабочего колеса нормального к оси турбины. Таким образом, имеем Как видно из этого уравнения, выход будет нормальным при: Если различные режимы (различные расходы Q и числа оборотов n) представить точками плоскости, то нормальный выход из турбины будет при режимах, находящихся на прямой ОВ, выходящей из начала координат (рисунок 4.9). Все режимы выше этой прямой будут, как видно из последнего уравнения для vU2, давать положительную закрутку (в направлении вращения турбины), так как vU2 > 0, а ниже прямой — отрицательную, т Рисунок 4.10. Скорости на входной и выходной кромках лопастей рабочего колеса Протекающая через рабочее колесо за время dtмасса жидкости В этих условиях закон момента количества движения представляется формулой: ρQ(v1Ur1 — v2Ur2) = ∑Mo
В последнем случае обе группы сил дают момент относительно оси, но первую из-за малости можно не учитывать, и тогда остается момент, воздействующий на жидкость со стороны лопастей рабочего колеса М. Искомый же момент рабочего колеса, создаваемый жидкостью на лопастях, будет равен — М. Далее используя выражения средней циркуляции: можно выразить момент рабочего колеса через разность средних циркуляции на входе и выходе: Последняя формула особенно наглядна. Она показывает, что на рабочем колесе создается крутящий момент только в том случае, когда оно воздействием своих лопастей изменяет циркуляцию потока. Знак Г принимается положительным, если vu совпадает с направлением окружной скорости u. Зная момент и задавая угловую скорость рабочего колеса, можно определить развиваемую им мощность: Здесь: М – в Н•м, ω – в 1/с, Npк – в Вт. В то же время известно, что мощность турбины выражается формулой Npк = ρgQHη. Это позволяет составить равенство: или с учетом циркуляции: Данные формулы представляют собой основное уравнение турбин, или уравнение Л. Эйлера. Левая часть HηГ — энергия в Дж, полученная рабочим колесом от жидкости весом в 1 Н, прошедшей через лопастную систему рабочего колеса. Правая часть содержит кинематические параметры потока при входе на рабочее колесо и после выхода из него. Таким образом, основное уравнение дает связь между энергетическими и кинематическими параметрами в турбине. Из последнего уравнения Эйлера можно сделать важные выводы: 1.Выше отмечалось, что наиболее благоприятный по КПД режим работы близок к условиям нормального выхода, когда циркуляция Г2 = 0 или мала. При этом, Г1 = ГО – циркуляции, создаваемые направляющим аппаратом. Отсюда можно определить требуемое значение ГО в зависимости от Н и ω. 2. В процессе прохождения воды через рабочее колесо турбины 4.3.2 Уравнение Бернулли для относительного движения. Представляет интерес другой вывод уравнения Л.Эйлера, позволяющий несколько глубже понять механизм преобразования энергии рабочим колесом турбины, а именно вывод, основанный на уравнении Бернулли. Однако в данном случае нужно использовать уравнение Бернулли, записанное для относительного движения w. Представим себе что имеется диск, вращающийся с частотой n, (об/мин), на высоте z над плоскостью сравнения 0 – 0, рисунок 4.11. На диске укреплена трубка 1 – 2. По трубке от сечения 1 к сечению 2 движется жидкость с относительной скоростью w (относительно трубки). Рисунок 4.11. К уравнению Бернулли для относительного движения В данном случае уравнение Бернулли для плоскости сравнения 0-0 имеет вид: Здесь h1 — 2 — потери напора на участке 1 – 2; u1 и u2 — окружные скорости (переносные). Особенность состоит в том, что в рассматриваемых условиях удельная энергия жидкости при движении вдоль трубки может убывать или возрастать в зависимости от изменения переносной скорости u1 и u2. Это свойство и используется в рабочем колесе турбины, каналы которого, образованные лопастями, представляют собой систему «трубок». Из этого уравнения следует, что: Удельная энергия жидкости при входе на рабочее колесо: Удельная энергия жидкости при сходе с рабочего колеса: Разность удельных энергий: e1 – e2 = Заменив выражение в скобках на выражение правой части (2), получим: НР.К. = НР.К. = Это выражение основного уравнения турбины объясняет связь формы рабочего колеса с напором турбины. В осевых турбинах u1 = u2 и, следовательно, H·ηГ определяется только абсолютными и относительными скоростями, которые не могут быть слишком большими, так как иначе возрастут потери. Это и вызывает ограничение использования осевых турбин по напору. С ростом Н переходят на диагональные и радиально-осевые турбины, у которых действует и различие переносных скоростей u1иu2, причем чем больше Н, тем роль этого фактора возрастает. Этим объясняется то, что у высоконапорных турбин увеличивается отношение D1 / D2 (см. рисунок 7.3). Источник |


 =
=

 ак как vU2
ак как vU2 


 (1)
(1) (2)
(2)











