Вывести номер минимального элемента массива matlab

Y = min(X)
[Y, I] = min(X)
C = min(A, B)

Функция Y = min(X) в случае одномерного массива возвращает наименьший элемент; в случае двумерного массива — это вектор-строка, содержащая минимальные элементы каждого столбца. Таким образом, min(min(X)) — это наименьший элемент массива.

Функция [Y, I] = min(X) кроме самих минимальных элементов возвращает вектор-строку индексов этих элементов в данном столбце.

Функция C = min(A, B) возвращает массив C тех же размеров, какие имеют массивы A и B, каждый элемент которого есть минимальный из соответствующих элементов этих массивов.

Если анализируемый массив содержит комплексные элементы, то минимальные элементы определяются из условия min(abs(X)). Если массив содержит один или несколько элементов типа NaN, то результатом операции min будет NaN.

Пример:

Рассмотрим массив M = magic(3).

M =	8	1	6
3	5	7
4	9	2

y = min(M)	[y, I] = min(M)	min(min(M))
y = 3 1 2	y = 3 1 2 I = 2 1 3	1

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Урок 5 — Работа с массивами в Матлаб(Matlab)

Все данные MatLab представляет в виде массивов. Очень важно правильно понять, как использовать массивы. Без этого невозможна эффективная работа в MatLab, в частности построение графиков, решение задач линейной алгебры, обработки данных, статистики и многих других. В данном подразделе описаны вычисления с векторами.

Массив — упорядоченная, пронумерованная совокупность однородных данных. У массива должно быть имя. Массивы различаются по числу размерностей или измерений: одномерные, двумерные, многомерные. Доступ к элементам осуществляется при помощи индекса. В MatLab нумерация элементов массивов начинается с единицы. Это значит, что индексы должны быть больше или равны единице.

Важно понять, что вектор, вектор-строка или матрица являются математическими объектами, а одномерные, двумерные или многомерные массивы — способы хранения этих объектов в компьютере. Всюду дальше будут использоваться слова вектор и матрица, если больший интерес представляет сам объект, чем способ его хранения. Вектор может быть записан в столбик (вектор-столбец) и в строку (вектор-строка). Вектор-столбцы и вектор-строки часто будут называться просто векторами, различие будет сделано в тех случаях, если важен способ хранения вектора в MatLab. Векторы и матрицы обозначаются курсивом, а соответствующие им массивы прямым моноширинным шрифтом, например: «вектор а содержится в массиве а», «запишите матрицу R в массив r».

Ввод сложение и вычитание векторов

Работу с массивами начнем с простого примера — вычисления суммы векторов: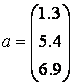
, .

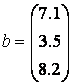
Для хранения векторов используйте массивы а и b. Введите массив а в командной строке, используя квадратные скобки и разделяя элементы вектора точкой с запятой:

» a = [1.3; 5.4; 6.9]
a =
1.3000
5.4000
6.9000

Так как введенное выражение не завершено точкой с запятой, то пакет MatLab автоматически вывел значение переменной а. Введите теперь второй вектор, подавив вывод на экран

Для нахождения суммы векторов используется знак +. Вычислите сумму, запишите результат в массив с и выведите его элементы в командное окно:

» с = а + b
с =
8.4000
8.9000
15.1000

Узнайте размерность и размер массива а при помощи встроенных функций ndims и size:

Итак, вектор а хранится в двумерном массиве а размерностью три на один (вектор-столбец из трех строк и одного столбца). Аналогичные операции можно проделать и для массивов b и c. Поскольку числа в пакете MatLab представляются в виде двумерного массива один на один, то при сложении векторов используется тот же знак плюс, что и для сложения чисел.

Ввод вектор-строки осуществляется в квадратных скобках, однако элементы следует разделять пробелами или запятыми. Операции сложения, вычитания и вычисление элементарных функций от вектор-строк производятся так же, как и с вектор-столбцами, в результате получается вектор-строка того же размера, что и исходные. Например:

» s1 = [3 4 9 2]
s1 =
3 4 9 2
» s2 = [5 3 3 2]
s1 =
5 3 3 2
» s3 = s1 + s2
s3 =
8 7 12 4

Замечание 1

Если размеры векторов, к которым применяется сложение или вычитание, не совпадают, то выдается сообщение об ошибке.

Естественно, для нахождения разности векторов следует применять знак минус, с умножением дело обстоит несколько сложнее.
Введите две вектор-строки:

» v1 = [2 -3 4 1];
» v2 = [7 5 -6 9];

Операция .* (не вставляйте пробел между точкой и звездочкой!) приводит к поэлементному умножению векторов одинаковой длины. В результате получается вектор с элементами, равными произведению соответствующих элементов исходных векторов:

» u = v1.*v2
u =
14 -15 -24 9

При помощи .^ осуществляется поэлементное возведение в степень:

» р = v1.^2
p =
4 9 16 1

Показателем степени может быть вектор той же длины, что и возводимый в степень. При этом каждый элемент первого вектора возводится в степень, равную соответствующему элементу второго вектора:

» p = vl.^v2
Р =
128.0000 -243.0000 0.0002 1.0000

Деление соответствующих элементов векторов одинаковой длины выполняется с использованием операции ./

» d = v1./v2
d =
0.2857 -0.6000 -0.6667 0.1111

Обратное поэлементное деление (деление элементов второго вектора на соответствующие элементы первого) осуществляется при помощи операции .\

» dinv = vl.\v2
dinv =
3.5000 -1.6667 -1.5000 9.0000

Итак, точка в MatLab используется не только для ввода десятичных дробей, но и для указания того, что деление или умножение массивов одинакового размера должно быть выполнено поэлементно.
К поэлементным относятся и операции с вектором и числом. Сложение вектора и числа не приводит к сообщению об ошибке. MatLab прибавляет число к каждому элементу вектора. То же самое справедливо и для вычитания:

» v = [4 6 8 10];
» s = v + 1.2
s =
5.2000 6.2000 9.2000 11.2000
» r = 1.2 — v
r =
-2.8000 -4.8000 -6.8000 -8.8000
» r1 = v — 1.2
r1 = 2.8000 4.8000 6.8000 8.8000

Умножать вектор на число можно как справа, так и слева:

» v = [4 6 8 10];
» p = v*2
р =.
8 12 16 20
» pi = 2*v
pi =
8 12 16 20

Делить при помощи знака / можно вектор на число:

» р = v/2
p =
2 3 4 5

Попытка деления числа на вектор приводит к сообщению об ошибке:

» р = 2/v
. Error using ==> /
Matrix dimensions must agree.

Если требуется разделить число на каждый элемент вектора и записать результат в новый вектор, то следует использовать операцию ./

» w = [4 2 6];
» d = 12./w
d =
3 6 2

Все вышеописанные операции применимы как к вектор-строкам, так и к вектор-столбцам.
Особенность MatLab представлять все данные в виде массивов является очень удобной. Пусть, например, требуется вычислить значение функции sin сразу для всех элементов вектора с (который хранится в массиве с) и записать результат в вектор d. Для получения вектора d достаточно использовать один оператор присваивания:

» d = sin(с)
d =
0.8546
0.5010
0.5712

Итак, встроенные в MatLab элементарные функции приспосабливаются к виду аргументов; если аргумент является массивом, то результат функции будет массивом того же размера, но с элементами, равными значению функции от соответствующих элементов исходного массива. Убедитесь в этом еще на одном примере. Если необходимо найти квадратный корень из элементов вектора dсо знаком минус, то достаточно записать:

» sqrt(-d)
ans =
0 + 0.9244i
0 + 0.7078i
0 + 0.7558i

Оператор присваивания не использовался, поэтому пакет MatLab записал ответ в стандартную переменную ans.

Для определения длины вектор-столбцов или вектор-строк служит встроенная функция length:

Из нескольких вектор-столбцов можно составить один, используя квадратные скобки и разделяя исходные вектор-столбцы точкой с запятой:

Для сцепления вектор-строк также применяются квадратные скобки, но сцепляемые вектор-строки отделяются пробелами или запятыми:

» v1 = [1 2];
» v2 = [3 4 5];
» v = [v1 v2]
v =
1 2 3 4 5

Работа с элементами векторов

Доступ к элементам вектор-столбца или вектор-строки осуществляется при помощи индекса, заключаемого в круглые скобки после имени массива, в котором хранится вектор. Если среди переменных рабочей среды есть массив v, определенный вектор-строкой

» v = [1.3 3.6 7.4 8.2 0.9];

то для вывода, например его четвертого элемента, используется индексация:

Появление элемента массива в левой части оператора присваивания приводит к изменению в массиве

» v(2) = 555
v =
1.3000 555.0000 7.4000 8.2000 0.9000

Из элементов массива можно формировать новые массивы, например

» u = [v(3); v(2); v(1)]
u =
7.4000
555.0000
1.3000

Для помещения определенных элементов вектора в другой вектор в заданном порядке служит индексация при помощи вектора. Запись в массив w четвертого, второго и пятого элементов v производится следующим образом:

» ind = [4 2 5];
» w = v(ind)
w =
8.2000 555.0000 0.9000

MatLab предоставляет удобный способ обращения к блокам последовательно расположенных элементов вектор-столбца или вектор-строки. Для этого служит индексация при помощи знака двоеточия. Предположим, что в массиве w, соответствующем вектор-строке из семи элементов, требуется заменить нулями элементы со второго по шестой. Индексация при помощи двоеточия позволяет просто и наглядно решить поставленную задачу:

» w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8];
» w(2:6) = 0;
» w
w =
0.1000 0 0 0 0 0 9.8000

Присваивание w(2:6) = 0 эквивалентно последовательности команд
w(2) = 0; w(3)=0; w(4)=0; w(5)=0; w(6)=0.
Индексация при помощи двоеточия оказывается удобной при выделении части из большого объема данных в новый массив:

» w — [0.1 2.9 3.3 5.1 2.6 7.1 9.8];
» wl = w(3:5)
wl =
3.3000 5.1000 2.6000

Составьте массив w2, содержащий элементы w кроме четвертого. В этом случае удобно использовать двоеточие и сцепление строк:

» w2 = [w(l:3) w(5:7)]
w2 =
0.1000 2.9000 3.3000 2.6000 7.1000 9.8000

Элементы массива могут входить в выражения. Нахождение, например среднего геометрического из элементов массива u, можно выполнить следующим образом:

Конечно, этот способ не очень удобен для длинных массивов. Для того чтобы найти среднее геометрическое, необходимо набрать в формуле все элементы массива. В MatLab существует достаточно много специальных функций, облегчающих подобные вычисления.

Применение функций обработки данных к векторам

Перемножение элементов вектора-столбца или вектора-строки осуществляется при помощи функции prod:

» z = [3; 2; 1; 4; 6; 5];
» р = prod(z)
p = 720

Функция sum предназначена для суммирования элементов вектора. С ее помощью нетрудно вычислить среднее арифметическое элементов вектора z:

» sum(z)/length(z)
ans =
3.5000

В MatLab имеется и специальная функция mean для вычисления среднего арифметического:

Для определения минимального и максимального из элементов вектора служат встроенные функции min и max:

» m1 = max(z)
m1 =
6
» m2 = min(z)
m2 =
1

Часто необходимо знать не только значение минимального или максимального элемента в массиве, но и его индекс (порядковый номер). В этом случае встроенные функции min и max необходимо использовать с двумя выходными аргументами, например

» [m, k] = min(z)
m =
1
k =
3

В результате переменной m будет присвоено значение минимального элемента массива z, а номер минимального элемента занесен в переменную k.
Для получения информации о различных способах использования функций следует набрать в командной строке help и имя функции. MatLab выведет в командное окно всевозможные способы обращения к функции с дополнительными пояснениями.
В число основных функций для работы с векторами входит функция упорядочения вектора по возрастанию его элементов sort.

» r = [9.4 -2.3 -5.2 7.1 0.8 1.3];
» R = sort(r)
R =
-5.2000 -2.3000 0.8000 1.3000 7.1000 9.4000

Можно упорядочить вектор по убыванию, используя эту же функцию sort:

» R1 = -sort(-r)
R1 =
9.4000 7.1000 1.3000 0.8000 -2.3000 -5.2000

Упорядочение элементов в порядке возрастания их модулей производится с привлечением функции abs:

» R2 = sort(abs(r))
R2 =
0.8000 1.3000 2.3000 5.2000 7.1000 9.4000

Вызов sort с двумя выходными аргументами приводит к образованию массива индексов соответствия элементов упорядоченного и исходного массивов:

» [rs, ind] = sort(r)
rs =
-5.2000 -2.3000 0.8000 1.3000 7.1000 9.4000
ind =
3 2 5 6 4 1

Источник

Документация

Минимальные элементы массива

Синтаксис

Описание

M = min( A ) возвращает минимальные элементы массива.

Если A вектор, затем min(A) возвращает минимум A .

Если A матрица, затем min(A) вектор-строка, содержащий минимальное значение каждого столбца.

Если A многомерный массив, затем min(A) действует вдоль первого измерения массива, размер которого не равняется 1 , обработка элементов как векторы. Размер этой размерности становится 1 в то время как размеры всех других размерностей остаются то же самое. Если A пустой массив с первой размерностью 0 , затем min(A) возвращает пустой массив с тем же размером как A .

M = min( A ,[], dim ) возвращает минимальный элемент по измерению dim . Например, если A матрица, затем min(A,[],2) вектор-столбец, содержащий минимальное значение каждой строки.

M = min( A ,[], nanflag ) задает, включать ли или не использовать NaN значения в вычислении. Например, min(A,[],’includenan’) включает весь NaN значения в A в то время как min(A,[],’omitnan’) игнорирует их.

M = min( A ,[], dim , nanflag ) также задает размерность, которую задает направление расчета при использовании nanflag опция.

[ M , I ] = min( ___ ) также возвращает индекс в операционную размерность, которая соответствует минимальному значению A для любого из предыдущих синтаксисов.

M = min( A ,[], ‘all’ ) находит минимум по всем элементам A . Этот синтаксис допустим для MATLAB ® версии R2018b и позже.

M = min( A ,[], vecdim ) вычисляет минимум по размерностям, заданным в векторном vecdim . Например, если A матрица, затем min(A,[],[1 2]) вычисляет минимум по всем элементам в A , поскольку каждый элемент матрицы содержится в срезе массивов, заданном размерностями 1 и 2.

M = min( A ,[], ‘all’ , nanflag ) вычисляет минимум по всем элементам A при использовании nanflag опция.

M = min( A ,[], vecdim , nanflag ) задает несколько размерностей, которых задают направление расчета при использовании nanflag опция.

[ M , I ] = min( A ,[], ‘all’ , ___ ) возвращает линейный индекс в A это соответствует минимальному значению в A при определении ‘all’ .

[ M , I ] = min( A ,[], ___ ,’linear’) возвращает линейный индекс в A это соответствует минимальному значению в A .

C = min( A , B ) возвращает массив с самыми маленькими элементами, взятыми из A или B .

C = min( A , B , nanflag ) также задает, как обработать NaN значения.

___ = min( ___ ,’ComparisonMethod’, method ) опционально задает, как сравнить элементы для любого из предыдущих синтаксисов. Например, для векторного A = [-1 2 -9] , синтаксис min(A,[],’ComparisonMethod’,’abs’) сравнивает элементы A согласно их абсолютным значениям и возвращает -1 .

Примеры

Самый маленький векторный элемент

Создайте вектор и вычислите его самый маленький элемент.

Самый маленький комплексный элемент

Создайте комплексный вектор и вычислите его самый маленький элемент, то есть, элемент с наименьшей величиной.

Самый маленький элемент в каждом столбце матрицы

Создайте матрицу и вычислите самый маленький элемент в каждом столбце.

Самый маленький элемент в каждой матричной строке

Создайте матрицу и вычислите самый маленький элемент в каждой строке.

Самое маленькое включение элемента NaN

Создайте вектор и вычислите его минимум, исключая NaN значения.

min(A) также приведет к этому результату начиная с ‘omitnan’ опция по умолчанию.

Используйте ‘includenan’ отметьте, чтобы возвратить NaN .

Самые маленькие индексы элемента

Создайте матричный A и вычислите самые маленькие элементы в каждом столбце, а также индексах строки A в котором они появляются.

Минимум страницы массивов

Создайте трехмерный массив и вычислите минимум по каждой странице данных (строки и столбцы).

Начиная в R2018b, вычислять минимум по всем размерностям массива, можно или задать каждую размерность в векторном аргументе размерности или использовать ‘all’ опция.

Возвратите линейные индексы

Создайте матричный A и возвратите минимальное значение каждой строки в матричном M . Используйте ‘linear’ опция, чтобы также возвратить линейные индексы I таким образом, что M = A(I) .

Самое маленькое сравнение элемента

Создайте матрицу и возвратите наименьшее значение между каждым из его элементов по сравнению со скаляром.

Входные параметры

A — Входной массив
скаляр | вектор | матрица | многомерный массив

Входной массив, заданный как скалярный, векторный, матричный или многомерный массив.

Если A является комплексным, затем min(A) возвращает комплексное число с наименьшей величиной. Если величины равны, то min(A) возвращает значение с наименьшей величиной и самым маленьким углом фазы.

Если A скаляр, затем min(A) возвращает A .

Если A пустой массив 0 на 0, затем min(A) также.

Если A имеет вводят categorical , затем это должно быть порядковым.

dim — Размерность, которая задает направление расчета
положительный целочисленный скаляр

Величина для работы, заданная как положительный целый скаляр. Если значение не задано, то по умолчанию это первый размер массива, не равный 1.

Размерность dim указывает на размерность, длина которой уменьшает до 1 . size(M,dim) 1 , в то время как размеры всех других размерностей остаются то же самое, если size(A,dim) 0 . Если size(A,dim) 0 , затем min(A,dim) возвращает пустой массив с тем же размером как A .

Рассмотрите двумерный входной массив, A :

Если dim = 1 , затем min(A,[],1) возвращает вектор-строку, содержащий самый маленький элемент в каждом столбце.

Если dim = 2 , затем min(A,[],2) возвращает вектор-столбец, содержащий самый маленький элемент в каждой строке.

min возвращает A если dim больше ndims(A) .

vecdim — Вектор из размерностей
вектор из положительных целых чисел

Вектор из размерностей в виде вектора из положительных целых чисел. Каждый элемент представляет размерность входного массива. Продолжительности выхода в заданных операционных размерностях равняются 1, в то время как другие остаются то же самое.

Рассмотрите 2 3х3 входным массивом, A . Затем min(A,[],[1 2]) возвращает 1 1 3 массивами, элементами которых являются минимумы, вычисленные по каждой странице A .

B — Дополнительный входной массив
скаляр | вектор | матрица | многомерный массив

Дополнительный входной массив в виде скаляра, вектора, матрицы или многомерного массива. Входные параметры A и B должен или быть одного размера или иметь размеры, которые совместимы (например, A M — N матрица и B скаляр или 1 — N вектор-строка). Для получения дополнительной информации см. «Совместимые размеры массивов для основных операций».

A и B должен быть совпадающий тип данных, если каждый не double . В этом случае типом данных другого массива может быть single длительность , или любой целочисленный тип.

Если A и B порядковый categorical массивы, у них должны быть те же наборы категорий с тем же порядком.

nanflag NaN условие
‘omitnan’ (значение по умолчанию) | ‘includenan’

NaN условие в виде одного из этих значений:

‘omitnan’ — Проигнорируйте весь NaN значения во входе. Если всеми элементами является NaN , затем min возвращает первый.

‘includenan’ — Включайте NaN значения во входе для вычисления.

Для datetime массивы, можно также использовать ‘omitnat’ или ‘includenat’ не использовать и включать NaT значения, соответственно.

Для categorical массивы, можно также использовать ‘omitundefined’ или ‘includeundefined’ не использовать и включать неопределенные значения, соответственно.

Типы данных: char

method ‘ComparisonMethod’
‘auto’ (значение по умолчанию) | ‘real’ | ‘abs’

Метод сравнения для числового входа в виде одного из этих значений:

‘auto’ — Для числового входного массива A , сравните элементы real(A) когда A действительно, и abs(A) когда A является комплексным.

‘real’ — Для числового входного массива A , сравните элементы real(A) когда A является действительным или комплексным. Если A имеет элементы с равными действительными частями, затем используйте imag(A) повредить связи.

‘abs’ — Для числового входного массива A , сравните элементы abs(A) когда A является действительным или комплексным. Если A имеет элементы с равной величиной, затем используйте angle(A) в интервале (-π,π], чтобы повредить связи.

Выходные аргументы

M — Минимальные значения
скаляр | вектор | матрица | многомерный массив

Минимальные значения, возвращенные как скаляр, вектор, матрица или многомерный массив. size(M,dim) 1 , в то время как размеры всех других размерностей совпадают с размером соответствующей размерности в A , если size(A,dim) 0 . Если size(A,dim) 0 , затем M пустой массив с тем же размером как A .

I — Индекс
скаляр | вектор | матрица | многомерный массив

Индексируйте, возвращенный как скаляр, вектор, матрица или многомерный массив. I одного размера с первым выходом.

Когда ‘linear’ не задан, I индекс в операционную размерность. Когда ‘linear’ задан, I содержит линейные индексы A соответствие минимальным значениям.

Если самый маленький элемент происходит несколько раз, то I содержит индекс к первому вхождению значения.

C — Минимальные элементы от A или B
скаляр | вектор | матрица | многомерный массив

Минимальные элементы от A или B , возвращенный как скаляр, вектор, матрица или многомерный массив. Размер C определяется неявным расширением размерностей A и B Для получения дополнительной информации см. «Совместимые размеры массивов для основных операций».

Тип данных C зависит от типов данных A и B :

Если A и B совпадающий тип данных, затем C совпадает с типом данных A и B .

Если любой A или B single , затем C single .

Если любой A или B целочисленный тип данных с другим скалярный double , затем C принимает целочисленный тип данных.

Расширенные возможности

«Высокие» массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Указания и ограничения по применению:

Если вы задаете пустой массив для второго аргумента для того, чтобы предоставить dim или nanflag , второй аргумент должен иметь фиксированный размер и размерности 0 — 0 .

Если вы задаете dim или nanflag , затем они должны быть константами.

Если вход является массивом переменного размера, длина размерности, которой задает направление расчета не должна быть нулем во времени выполнения.

Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.

Указания и ограничения по применению:

Если вы задаете dim или nanflag , затем они должны быть константами.

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool .

Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает массивы графического процессора. Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox) .

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает распределенные массивы. Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox) .

Смотрите также

Открытый пример

У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?

Документация MATLAB

Поддержка

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста — например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

Источник

Вывести номер минимального элемента массива matlab