Вывести матрицу по порядку

Клёвый код

Скриптописание и кодинг

Решаем задачи Абрамян на C. Matrix78

Matrix78. Дана матрица размера $$M \times N$$. Упорядочить ее строки так, чтобы их минимальные элементы образовывали убывающую последовательность.

Решаем задачи Абрамян на C. Matrix77

Matrix77. Дана матрица размера $$M \times N$$. Упорядочить ее столбцы так, чтобы их последние элементы образовывали убывающую последовательность.

Решаем задачи Абрамян на C. Matrix76

Matrix76. Дана матрица размера $$M \times N$$. Упорядочить ее строки так, чтобы их первые элементы образовывали возрастающую последовательность.

Решаем задачи Абрамян на C. Matrix75

Matrix75. Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным максимумом, если он больше всех окружающих его элементов. Поменять знак всех локальных максимумов данной матрицы на противоположный. При решении допускается использовать вспомогательную матрицу.

Решаем задачи Абрамян на C. Matrix74

Matrix74. Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным минимумом, если он меньше всех окружающих его элементов. Заменить все локальные минимумы данной матрицы на нули. При решении допускается использовать вспомогательную матрицу.

Решаем задачи Абрамян на C. Matrix73

Matrix73. Дана матрица размера $$M \times N$$. После последнего столбца, содержащего только отрицательные элементы, вставить столбец из нулей. Если требуемых столбцов нет, то вывести матрицу без изменений.

Решаем задачи Абрамян на C. Matrix72

Matrix72. Дана матрица размера $$M \times N$$. Перед первым столбцом, содержащим только положительные элементы, вставить столбец из единиц. Если требуемых столбцов нет, то вывести матрицу без изменений.

Решаем задачи Абрамян на C. Matrix71

Matrix71. Дана матрица размера $$M \times N$$. Продублировать столбец матрицы, содержащий ее минимальный элемент.

Решаем задачи Абрамян на C. Matrix70

Matrix70. Дана матрица размера $$M \times N$$. Продублировать строку матрицы, содержащую ее максимальный элемент.

Решаем задачи Абрамян на C. Matrix69

Matrix69. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. После столбца матрицы с номером $$K$$ вставить столбец из единиц.

Источник

Вывести элементы матрицы в порядке их следования по диагоналям матрицы

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Вывести элементы квадратной матрицы по диагоналям
Вывести элементы квадратной матрицы(по диагоналям(как на рисунке)

Переписать в массив B нулевые и кратные 5 элементы матрицы А в порядке их следования
Желательно со схемой и контрольным примером Огромное спасибо! Ввести 2-мерный массив А целого.

Вывести элементы матрицы в определённом порядке
Всем доброго дня. Прошу помочь в такой задачке: Должно быть выполнено на консоле. Вывести.

Вывести элементы матрицы в заданном порядке
Дана матрица размера M × N. Вывести ее элементы в следующем порядке: первый столбец сверху вниз.

Решение

ИМХО
Красота этой задачи в ее симметрии, а динамика — в развороте матрицы.

В то же время в предложенном условии подчеркивается прямоугольность, что губит симметрию, а упор на «динамический ввод», как вершину человеческого гения, настораживает. Вывод: пардон, но преп — нуб и плодит себе подобных.

Вывести элементы матрицы в определенном порядке
Дана матрица размера M*N. Вывести ее элементы в следуещем порядке: первая строка слева направо.

Вывести элементы матрицы в определенном порядке
Вывести элементы матрицы в следующем порядке: первая строка слева направо, вторая строка справа.

Вывести элементы матрицы в определённом порядке
Вывести на экран элементы заданной матрицы А (4; 4) в следующем порядке: а (4, 4); а (4, 3); а (4.

Вывести элементы матрицы в заданном порядке
Вызвало затруднение задача, помогите) Дана квадратная матрица A порядка M. Начиная с элемента.

Источник

Математика для чайников. Матрицы и основные действия над ними

1-й курс, высшая математика, изучаем матрицы и основные действия над ними. Здесь мы систематизируем основные операции, которые можно проводить с матрицами. С чего начать знакомство с матрицами? Конечно, с самого простого — определений, основных понятий и простейших операций. Заверяем, матрицы поймут все, кто уделит им хотя бы немного времени!

Определение матрицы

Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.

Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.

Элементы, для которых i=j (a11, a22, .. ) образуют главную диагональ матрицы, и называются диагональными.

Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.

Операции сложения и вычитания матриц

Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.

Вычитание выполняется по аналогии, только с противоположным знаком.

Умножение матрицы на число

На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:

Операция умножения матриц

Перемножить между собой удастся не все матрицы. Например, у нас есть две матрицы — A и B. Их можно умножить друг на друга только в том случае, если число столбцов матрицы А равно числу строк матрицы В. При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м столбце второго. Чтобы понять этот алгоритм, запишем, как умножаются две квадратные матрицы:

И пример с реальными числами. Умножим матрицы:

Операция транспонирования матрицы

Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:

Определитель матрицы

Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!

Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.

Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.

А если матрица три на три? Тут уже посложнее, но справиться можно.

Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

К счастью, вычислять определители матриц больших размеров на практике приходится редко.

Здесь мы рассмотрели основные операции над матрицами. Конечно, в реальной жизни можно ни разу так и не встретить даже намека на матричную систему уравнений или же наоборот — столкнуться с гораздо более сложными случаями, когда придется действительно поломать голову. Именно для таких случаев и существует профессиональный студенческий сервис. Обращайтесь за помощью, получайте качественное и подробное решение, наслаждайтесь успехами в учебе и свободным временем.

Источник

Сформировать и вывести матрицу

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Сформировать и вывести матрицу
Есть матрица 5 на 5, в основной диагонали только 1 , а остальные цифры идут по порядку от 1 до 21 .

Двумерные массивы. Сформировать и вывести матрицу на экран
Задача: Сформировать квадратную матрицу порядка n по заданному образцу . Вывод матрицы на экран.

Сформировать и вывести на экран матрицу А размерами N*M элементов
Сформировать и вывести на экран матрицу А размерами N*M элементов, у которой элементы первого и.

Сформировать квадратную матрицу; транспонировать матрицу и инвертировать порядок элементов каждой ее строки
Заданы два одномерных массива одинаковой длины: R и S.Сформировать квадратную матрицу A, каждый.

Каждый раз когда запускается программа, и каждый раз 8 новых рандомных чисел в строке и все 8 строчек каждый раз должны быть одинаковы между собой но с разными числами

Добавлено через 50 секунд
Каждый раз 8 новых рандомных чисел в строке и все 8 строчек каждый раз должны быть одинаковы между собой но с разными числами. Каждый раз когда запускается компилятор (F5).

Решение

Создать квадратную матрицу, сформировать новую матрицу такой же размерности путём транспонирования исходной
Создать квадратную матрицу размерности (30, 30). Заполнить её случайными целыми числами из.

Сформировать матрицу из случайных значений, подсчитать сумму её элементов, вывести матрицу и сумму на экран
Задание: Создать двумерный массив случайных чисел А.Найти сумму элементов массива.Вывести массив.

сформировать матрицу А и вывести её
С помощью генератора случайных чисел сформировать матрицу А и вывести её. Сформировать одномерный.

Сформировать и вывести матрицу
Задано кол-во строк и столбцов матрицы(не более 10) и действительные значения ее.

Сформировать и вывести матрицу по образцу
1.Сформировать и вывести следующие матрицы: 1 1 1 1 1 2 2 1 1 1 А= 2 2 2 1 1.

Источник

Матрицы в C++. Общие сведения

Матрица — это двумерный массив, каждый элемент которого имеет два индекса: номер строки и номер столбца, поэтому для работы с элементами матрицы необходимо использовать два цикла. Если значениями параметра первого цикла будут номера строк матрицы, то значениями параметрами второго — столбцы (или наоборот). Обработка матрицы заключается в том, что вначале поочередно рассматриваются элементы первой строки (столбца), затем второй и т.д. до последней.

Перед тем, как приступить к изучению алгоритмов обработки матриц, давайте рассмотрим, как описываются матрицы в C++. Двумерный массив можно объявить так:

тип имя_переменной [n] [m];

Здесь тип определяет тип элементов массива, имя_переменной — имя матрицы, n — количество строк, m — количество столбцов. Строки нумеруются от 0 до n-1, столбцы от 0 до m-1.

Например int h[10] [15];

Выше матрица целых чисел h, состоящая из 10 строк и 15 столбцов (строки нумеруются от 0 до 9, столбцы от 0 до 14).

Для обращения к элементу матрицы необходимо указать ее имя и в квадратных скобках номер строки, затем номер столбца. Например, h[2] [5].

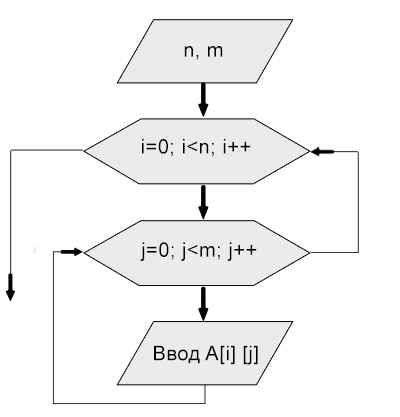
Ввод-вывод матриц

Матрицы, как и одномерные массивы, нужно вводить (выводить) поэлементно. Блок-схема ввода элементов матрицы A[n] [m] изображена ниже:

Код программы на Visual C++ вода-вывода матрицы будет иметь примерно такой вид:

Источник