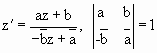Вывести формулы стереографической проекции

Стереографическая проекция ⁠

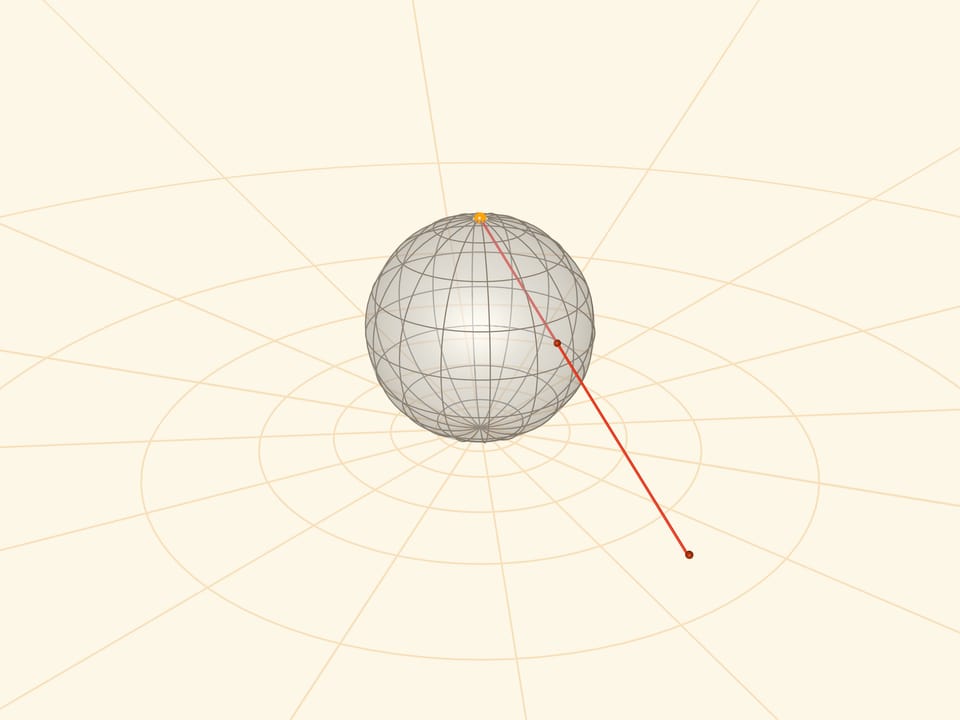
Сте­реографи­че­ская про­екция — это отоб­раже­ние сферы (с выко­ло­тым полю­сом) на плос­кость по сле­дующему закону. Для точки на сфере её образ на плос­ко­сти лежит на луче, соеди­няющем выко­ло­тый полюс сферы — центр про­екции — с точ­кой на сфере. Такое отоб­раже­ние вза­имно одно­знач­ное и «рабо­тает» в обе сто­роны.

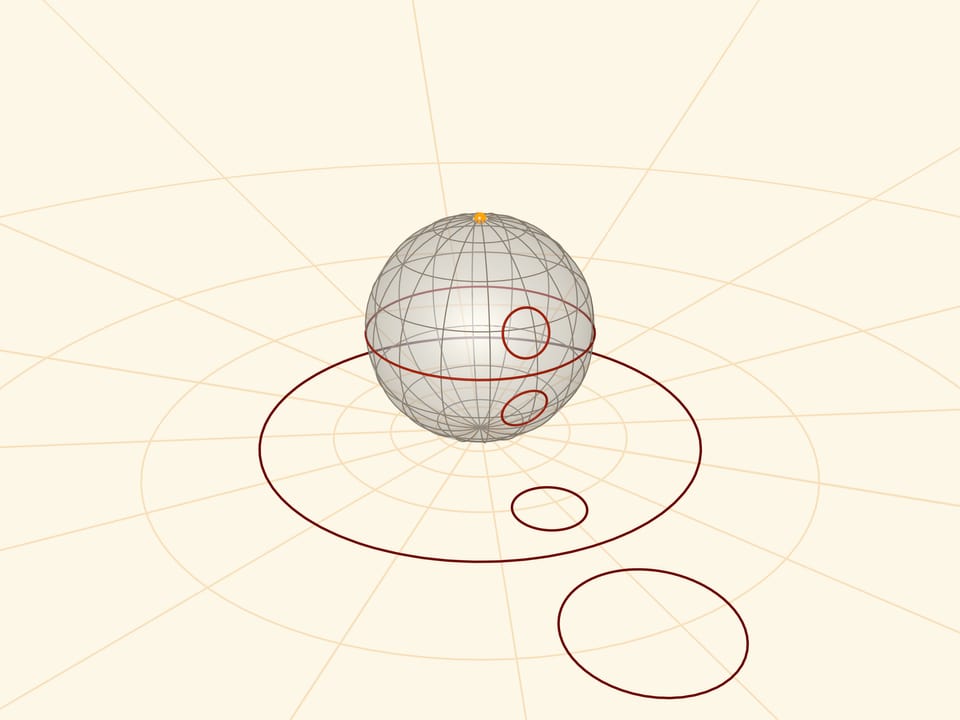
Сте­реографи­че­ская про­екция сохра­няет углы между лини­ями, а любые окруж­но­сти на сфере пере­во­дит в окруж­но­сти на плос­ко­сти. Точ­нее: окруж­но­сти, не про­хо­дящие через центр про­екции, пере­хо­дят в окруж­но­сти на плос­ко­сти, а про­хо­дящие через него (не только мери­ди­аны!) — в прямые.

Ещё одно свойство: симмет­рич­ные на сфере отно­си­тельно эква­тора кри­вые пере­хо­дят на плос­ко­сти в инверс­ные друг другу отно­си­тельно про­екция эква­тора.

Реа­ли­зо­вать сте­реографи­че­скую про­екцию можно поме­стив в полюс сферы небольшой (точеч­ный) источ­ник света.

Кра­си­вая модель: полоски на сфере, являющи­еся (про)обра­зом квад­рат­ной сетки на плос­ко­сти. Изго­то­вить её можно наклеив полоски на про­зрач­ную сферу или, что более кра­сиво, напе­ча­тав соот­вет­ствующую модель на 3D-прин­тере.

Лите­ра­тура

Segerman Henry . Visualizing Mathematics with 3D Printing. — [segerman.org]

Розенфельд Б. А. , Серге­ева Н. Д. Сте­реографи­че­ская про­екция. — М.: Наука, 1973. — (Попу­ляр­ные лекции по матема­тике; Вып. 53).

Мар­ку­ше­вич А. И. Комплекс­ные числа и конформ­ные отоб­раже­ния. — 2‐е изд. — М.: ГИФМЛ, 1960. — (Попу­ляр­ные лекции по матема­тике; Вып. 13). — [Стр. 29—31].

Пра­со­лов В. В. Задачи по сте­реомет­рии. — М.: МЦНМО, 2016. — [Гл. 20 «Инвер­сия и сте­реографи­че­ская про­екция»].

Кар­тографи­че­ские про­екции // Матема­ти­че­ская состав­ляющая / Ред.-сост. Н. Н. Андреев, С. П. Коно­ва­лов, Н. М. Паню­нин. — Вто­рое изда­ние, расши­рен­ное и допол­нен­ное. — М. : Матема­ти­че­ские этюды, 2019. — С. 136—145, 342, 343.

Источник

Лекция 1. 7 сентября 2016

Комплексные числа

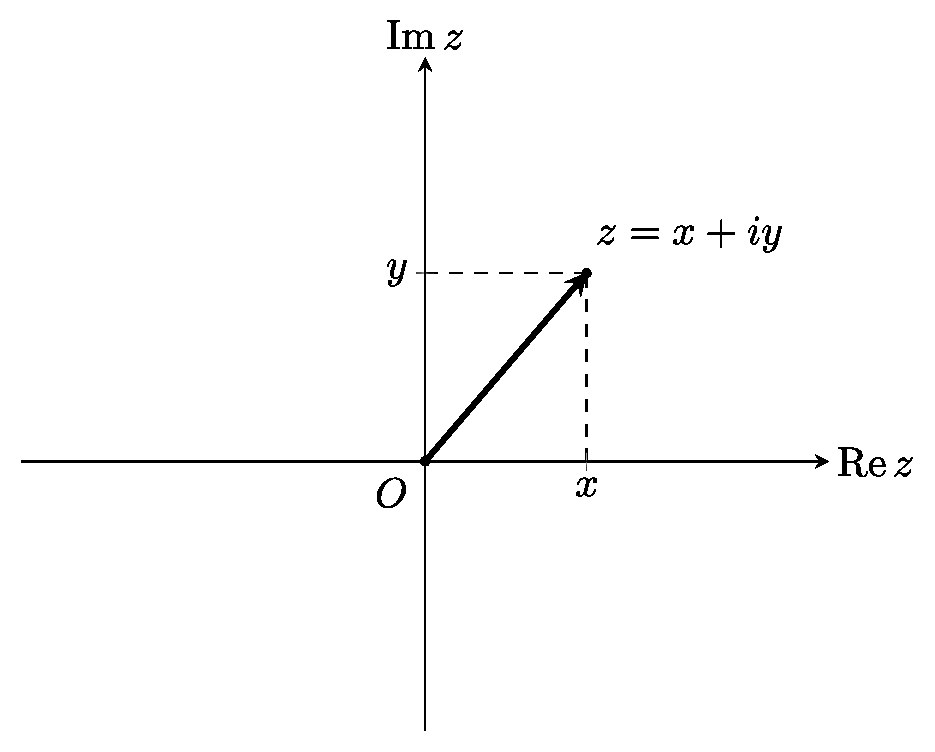
Комплексная плоскость

Рассмотрим плоскость и прямоугольную систему координат на ней. Ось абсцисс обозначим $\operatorname z$ и будем называть действительной осью, а ось ординат обозначим $\operatorname z$, будем называть мнимой осью. Каждому комплексному числу $z=x+iy$ сопоставим точку на этой плоскости с координатами $(x,y)$, и, другими словами, радиус-вектор с координатами $(x,y)$.

Заметим, что соответствие между комплексными числами и точками на комплесной плоскости является взаимнооднозначным соответствием (а в случае с вещественными числами, соответствие строится с точкам на вещественной прямой).

Геометрически сложение чисел $z_1$ и $z_2$ производится по правилу сложения векторов (по правилу параллелограмма).

Разность $z_1-z_2$ представляется вектором, конец которого находится в точке $z_1$, а начало — в точке $z_2$.

Комплексным сопряжением числа $z$ на комплексной плоскости является вектор, симметричный вектору $z$, относительно оси абсцисс.

Модуль комплексного числа $z=x+iy$ равен длине вектора, соответствующего данному числу на комплексной плоскости, $$|z|= \sqrt.$$ Несложно проверить, что расстояние между двумя точками комплексной плоскости $z_1$ и $z_2$ равно $|z_1-z_2|$. То есть, модуль разности двух комплексных чисел есть расстояние между точками на комплексной плоскости, которым соответствуют этим числам.

Полярные координаты

Любой вектор на плоскости полностью определяется своей длиной и углом с положительным направлением оси $Ox$. Модуль комплексного числа $$ \rho = |z| = \sqrt $$ это длина вектора $(x,y)$. Обозначим $\varphi = \operatorname z$ — аргумент комплексного числа $z$, при этом $$ x = \rho\cos\varphi, \qquad y = \rho\sin\varphi. $$

Отсюда можно вывести тригонометрическую запись $$ z = \rho(\cos\varphi + i\sin\varphi). $$ Строго говоря, аргумент комплексного числа определен не однозначно, в общем виде аргумент можно записать как \begin \operatorname z = \arg z + 2\pi k ,\text < где >k\in\mathbb Z, \end где $0\leq \arg z

Бесконечно удалённая точка

Введём понятие расширенной комплексной плоскости, состоящей из обычной комплексной плоскости и единственного бесконечно удалённого элемента -бесконечно удалённой точки $z = \infty$. Отметим, что аргумент комплексного числа $\infty$ не определён, так же как и его действительная и мнимая часть. Для комплексного числа $\infty$ полагают следующие алгебраические свойства:

$z\cdot\infty=\infty, \quad \text<при >z\ne0$;

Отметим, что так как $\dfrac<0><0>=0\cdot\dfrac<1><0>=0\cdot\infty$, то операция $\dfrac<0><0>$ также не определена.

Сфера Римана

Другим геометрическим представлением комплексных чисел является сфера Римана. Рассмотрим трехмерное евклидово пространство с координатами $(\xi,\eta,\theta)$ и совместим комплексную плоскость $\mathbb C$ с плоскостью $O\xi \eta$ так, чтобы действительная ось совпала с осью $, $ мнимая ось с осью $O<\eta>,$ и положительные направления на соответствующих осях совпадали. Обозначим через $S$ сферу с центром в точке $\left(0,0,\frac<1><2>\right)$ радиуса $\frac<1><2>$, имеющую уравнение \begin\label <\xi>^2+<\eta>^2+\left(\theta — \frac<1><2>\right)^2 =\frac<1><4>, \end а точку $(0,0,1)$ назовем \полюсом сферы $S$ и обозначим символом $P.$ Соединим отрезком точку $\mathbf\in \mathbb C$ с полюсом $P$, при этом отрезок пересечет сферу $S$ в единственной точке $M(\xi,\eta,\theta)$. Точка $M$ называется стереографической проекцией точки $\mathbf\in \mathbb C$ на сферу $S$.

Стереографическая проекция устанавливает взаимно однозначное соответствие между точками комплексной плоскости $\mathbb C$ и точками сферы $S$ с выколотым полюсом $P$. В силу колинеарности точек $P(0,0,1)$, $M(\xi,\eta,\theta)$ и $\mathbf(x,y,0)$ имеем $$\frac<\xi> = \frac<\eta> = \frac<1-\theta ><1>,$$ откуда выводим \begin\label x= \frac<\xi><1-\theta>, \ y= \frac<\eta><1-\theta>, z= \frac<\xi + i\eta><1-\theta>. \end Поскольку $$ |z|^2 = \frac<<\xi>^2 + <\eta>^2><(1-\theta)^2>, $$ то из уравнения сферы \eqref получаем \begin\label |z|^2 = \frac<\theta><1-\theta>. \end Выражая из равенства \eqref значение $\theta$ и подставляя его в равенства \eqref, находим \begin\label \xi = \frac<1+|z|^2>, \ \eta =\frac<1+|z|^2>, \ \theta = \frac<|z|^2><1+|z|^2>. \end Формулы \eqref называют формулами стереографической проекции. При неограниченном удалении точки $z$ от нуля в произвольном направлении (вдоль произвольной прямой) образ этой точки на сфере всегда будет стремиться к полюсу $P$. Если мы доопределим стереографическую проекцию, полагая полюс $P$ образом бесконечно удаленной точки, то получим взаимно однозначное соответствие между расширенной комплексной плоскостью $\overline<\mathbb C>$ и сферой $S$.

Упражнение. Доказать круговое свойство стереографической проекции: всякая окружность или прямая на комплексной плоскости $\mathbb C$ отображается стереографической проекцией в окружность на сфере $S$, и обратно, прообразом всякой окружности на сфере $S$ является либо окружность либо прямая на плоскости $\mathbb C$.

Упражнение. Доказать свойство консерватизма углов: угол между любыми гладкими кривыми на комплексной плоскости равен углу между образами этих кривых, лежащими на сфере $S$.

Кривые на комплексной плоскости

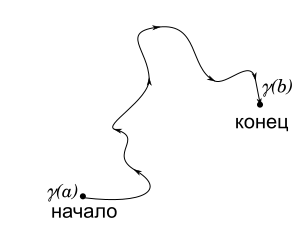
Пусть дана комплекснозначная функция $\gamma(t)$, непрерывная на отрезке $[a, b]$. Когда точка $t$ пробегает отрезок $[a, b]$, точка $\gamma(t) = x(t) + iy(t)$ пробегает некоторое множество в комплексной плоскости. Это множество вместе с указанием порядка, в котором проходятся все его точки, называется непрерывной кривой, а уравнение $z = \gamma(t)$ — параметрическим уравнением этой кривой. Порядок, в котором в котором проходятся точки называется ориентацией кривой.

Пример. Параметризация отрезка, соединяющего точки $z_1$ и $z_2$ имеет вид $$ \gamma(t) = z_1 + t\cdot(z_2-z_1), \qquad t\in[0,1]. $$ При этом кривая $\gamma$ ориентирована в направлении от $z_1$ к $z_2$.

Кривая, не имеющая самопересечений называется простой кривой или простым контуром.

Кривая называется замкнутой, если её начало совпадает с её концом, то есть если она имеет параметрическое уравнение \begin z = z(t),\quad a\leq t\leq b, \quad \text <для которого>\quad z(a) = z(b). \end

Пример. Одной из самых простых замкнутых кривых является окружность. Пусть $C(z_0,R)$ — окружность с центром в точке $z_0$ и радиусом $R$. Тогда параметризация этой окружности имеет вид $$ \gamma(t) = z_0 + Re^, \qquad t\in[0,2\pi]. $$ При этом кривая $\gamma$ ориентирована против часовой стрелки. Если требуется ориентация по часовой стрелке, то следует выбрать уравнение вида $$ \gamma(t) = z_0 + Re^<-it>, \qquad t\in[0,2\pi]. $$ Также приведём параметризацию эллипса $\frac+\frac=1$ $$ \gamma(t) = a\cos t + b\sin t, \qquad t\in[0,2\pi] $$ против часовой стрелки, и по часовой стрелке $$ \gamma(t) = a\cos t — b\sin t, \qquad t\in[0,2\pi]. $$

Если кривая $\gamma$ имеет хотя бы одно параметрическое уравнение $z = \gamma(t), \quad a\leq t\leq b$, с функцией $\gamma(t)$, имеющей на отрезке $[a, b]$ непрерывную и отличную от нуля производную, то $\gamma$ называется гладкой кривой.

Производная $\gamma'(t_0) = x'(t_0)+iy'(t_0)$ — является касательным вектором к кривой $\gamma$ в точке $\gamma(t_0)$. Непрерывная кривая $\gamma$ называется кусочно-гладкой кривой, если её можно разбить на конечное число частей, каждая из которых является гладкой кривой.

Топология комплексной плоскости

Приведём основные топологические понятия, которые потребуются в данном курсе. Пусть $z,w\in\mathbb C$, тогда $|z-w|$ — расстояние между точками $z$ и $w$. Расстояние от точки до множества и расстояние между множествами определяются следующим образом $$\operatorname(z, A) = \inf\limits_|z-w|, \quad \operatorname(A, B) = \inf\limits_|z-w|.$$ Фиксируем комплексное число $a\in\mathbb C$ и вещественное число $r>0$, тогда числа $z$, удовлетворяющие равенству $|a-z|=r$, составляют множество точек, удалённых от $a$ на расстояние $r$. Другими словами, это окружность с центром в $a$ и радиусом $r$.

Множество точек $B(a,r) = \

Также множество $B(a,r)$ называют окрестностью точки $a$ (или $r$-окрестностью). Однако $r$-окрестностью бесконечно удалённой точки называют множество $\overline<\mathbb C>\setminus \overline$, то есть внешность круга. Окрестностью бесконечно удалённой точки на сфере Римана является «шапочка», то есть часть сферы, расположенная выше некоторой плоскости $\theta=a$, \ $0

Пусть $E\subset\mathbb C$.
1. Точка $a$ называется внутренней точкой множества $E$, если найдётся окрестность $B(a, r)\subset E$.
2. Точка $b$ называется textbf <граничной точкой множества $E$, если всякая окрестность $B(b, r)$ содержит точки из $E$ и из $\mathbb C\setminus E$.
3. Точка $c$ называется предельной точкой множества $E$, если всякая окрестность $B(c, r)$ содержит точки из $E$, отличные от $c$.
4. Точка $d$ называется изолированной точкой множества $E$, если $d\in E$ и найдётся окрестность $B(d, r)$, которая не содержит других точек из $E$.

Множество $E\subset\mathbb C$ называется открытым, если все его точки внутренние. Множество $E\subset\mathbb C$ называется замкнутым, если оно содержит все свои граничные точки.

Пример. Пусть $R>0$ и $z_0\in\mathbb C$, тогда множества $\$ открыты, в то время как множество $\$ — замкнуто.

Пример. $\mathbb C$ и пустое множество $\emptyset$ — открытые множества (и в то же время замкнутые).

Множество всех граничных точек множества $E$ называется границей и обозначается $\partial E$. Множество всех внутренних точек множества $E$ называется внутренностью и обозначается $\operatorname E$. Объединение множества и его границы $\partial E\cup E$ называется замыканием и обозначается $\overline$.

Пример. Пусть $E = \ Связное множество

Область- это открытое связное множество.

Число компонент границы данной области называется\порядком связности этой области. Далее рассматриваются только области с конечным порядком связности, иными словами конечносвязные области.

Множество $E\subset\mathbb C$ называется ограниченным, если существует такой круг $B(0,R),\ R

Источник

Вывести формулы стереографической проекции

Стереографическая проекция

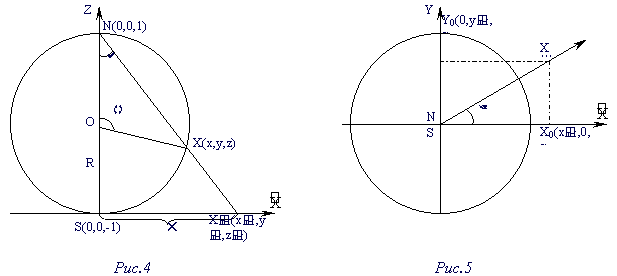
Пусть сфера единичного радиуса с центром в точке О (0, 0, 0) касается пополненной плоскости z=-1 в южном полюсе S(0, 0, -1).

Выберем на плоскости произвольно точку Х’ с координатами (х’, у’, -1). Полученная точка Х пересечения отрезка Х’N (рис.4) со сферой – стереографическая проекция точки Х’ на сферу. Обозначим ее координаты через (x, y, z) и найдем их.

Известно, что декартовы координаты точки через сферические выражаются следующими формулами:

x = R cos a sin q , y = R sin a sin q , z = R cos q .

Введем следующее обозначение: r = SX’. Тогда по рис. 5

, NX’= .

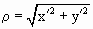
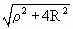
Рассмотрим D NOX. Применяя теорему синусов, получаем

.

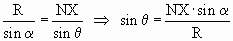
Рассматривая подобные треугольники NSX’ и NSX, получим, что

или .

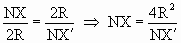
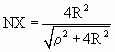
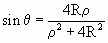
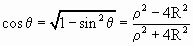
При этом . Следовательно .

По рис.4: .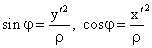

Таким образом, получаем координаты точки Х – стереографической проекции точки Х’:

, , .

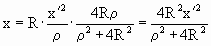
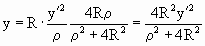
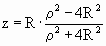
Но в нашем случае радиус сферы равен 1, тогда формулы приобретут вид:

, , .

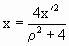
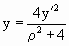
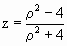
Пусть сфера единичного радиуса с центром в точке О (0, 0, 0) касается пополненной плоскости z=-1 в южном полюсе S(0, 0, -1).

Будем рассматривать конформные дробно-линейные преобразования, которые переводят окружность с координатами (x, y, -1) в окружность с координатами (х’ , у’, -1). Подвергнем ее конформному преобразованию вида

,

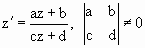
где a, b, c, d, z – комплексные.

Очевидно комплексная координата z = x+iy. Зная z, можем получить z’, а, следовательно, и координаты окружности, полученной в результате преобразования. При этом x’=Re(z), y’=Im(z).

Экваториальная плоскость

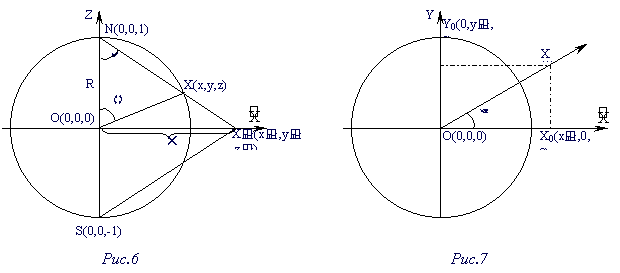
Пусть пополненная ХY-плоскость проходит через центр О(0,0,0) сферы единичного радиуса, т.е. является плоскостью экватора.

Выберем на плоскости произвольно точку Х’ с координатами (х’, у’, 0). Полученная точка Х пересечения отрезка Х’N (рис.6) со сферой – стереографическая проекция точки Х’ на сферу. Обозначим ее координаты через (x, y, z) и найдем их.

Снова применим сферические координаты точки, через которые можем найти ее декартовы координаты:

x = R cos a sin q , y = R sin a sin q , z = R cos q .

Введем следующее обозначение: r = ОX’. Тогда

, NX’= .

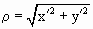
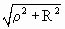
Рассмотрим D NOX. Применяя теорему синусов, получаем

.

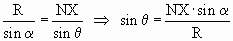
Рассматривая подобные треугольники NОX’ и NХS, получим, что

или .

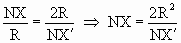
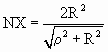
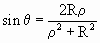
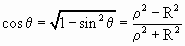
При этом . Следовательно .

По рис.7: .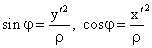

Таким образом, получаем координаты точки Х – стереографической проекции точки Х’:

, , .

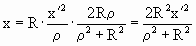
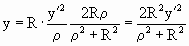
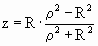
Но в нашем случае радиус сферы равен 1, тогда формулы приобретут вид:

, , . (1)

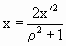
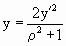
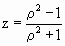
Как сказано выше, дробно-линейное конформное отображение вида

соответствует повороту на сфере SU(2)>SO(3).

Если b=0, то неподвижными точками являются z₁=0 и z₂=.

Если b0, то неподвижными будут точки . При чем х=Re(z) и y=Im(z).

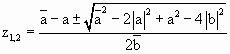
Пусть l, m, n координаты неподвижной точки на сфере, полученные применением преобразования (1) к точке (3).

Пусть (х’, y’, z’ ) – координаты стереографической проекции точки (x, y, 0). Пусть также точка (x₁, y₁, 0) – отображение точки (x, y, 0) конформным преобразованием (2), а (х», у», z» ) – стереографическая проекция точки (x₁, y₁, 0).

Расстояние между точками (х’, y’, z’ ) и (х», у», z»)

.

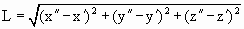
Расстояние от этих точек до прямой, проходящей через неподвижные точки на сфере (оси вращения) .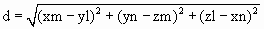

Угол поворота относительно оси вращения, переводящей (х’, y’, z’ ) в (х», у», z» ) .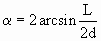

Список литературы

1. Бакельман И.Я. Высшая геометрия, М.: Просвещение, — 1967 г.
2. Постников М.М. Аналитическая геометрия, М.: Наука – 1973 г.
3. Ф. Клейн Лекции об экосаэдре и решение уравнений пятой степени, М: 1989 г.
4. Дьяконов А.Г. Matlab 5, М: 2000 г.

В начало

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник