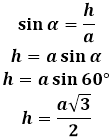Вывести формулу высоты равностороннего треугольника

Высота равностороннего треугольника

Равносторонний треугольник является правильным многоугольником (геометрическая фигура, у которой все углы и все стороны равны). Фактически, это значительно упрощает процесс вычисления любых параметров, характеризующих такой треугольник, в том числе, длину высоты.

В равностороннем треугольнике все три высоты — одинаковой длины, поэтому найдя любую из них, можно применять полученное значение в отношении всех трех линий. Более того, все высоты полностью совпадают со всеми тремя медианами, биссектрисами и серединными перпендикулярами, называемыми иначе медиатриссами. Точка пересечения всех трех линий обладает свойствами точки пересечения высот, точки пересечения медиан и точки пересечения биссектрис одновременно, являя собой любой из возможных центров треугольника, в том числе центр вписанной и описанной окружностей.

Исходя из этого, чтобы найти высоту равностороннего треугольника, можно использовать абсолютно любые известные параметры, например, сторону треугольника.

Высота равностороннего треугольника, проведенная к любой стороне, создает внутри него прямоугольный треугольник, в котором можно ее вычислить, используя тригонометрические отношения, так как известно, что все углы в равностороннем треугольнике имеют по 60 градусов. Для полученного прямоугольного треугольника высота будет катетом, противолежащем углу в 60 градусов, а сторона равностороннего треугольника — гипотенузой, соответственно, чтобы найти высоту, нужно применить синус. Если подставить вместо угла альфа 60 градусов, получится, что высота равностороннего треугольника равна половине стороны, умноженной на корень из трех.

Источник

Высота равностороннего треугольника

Средняя оценка: 4.7

Всего получено оценок: 110.

Средняя оценка: 4.7

Всего получено оценок: 110.

Равносторонний треугольник определяется всего одной величиной – значением стороны. Все стороны в таком треугольнике равны между собой, а углы известны заранее и равны 60 градусам каждый, поэтому чтобы посчитать любую характеристику или величину равностороннего треугольника достаточно знать его сторону. Убедимся в этом и выведем формулу высоты равностороннего треугольника.

Что такое равносторонний треугольник?

Для начала нужно вспомнить, что такое равносторонний треугольник, определить некоторые его свойства и только тогда выводить формулу высоты.

Равносторонний треугольник – это треугольник, все стороны которого равны между собой. Все углы в таком треугольнике равны между собой (60 градусов).

Рис. 1. Правильный треугольник.

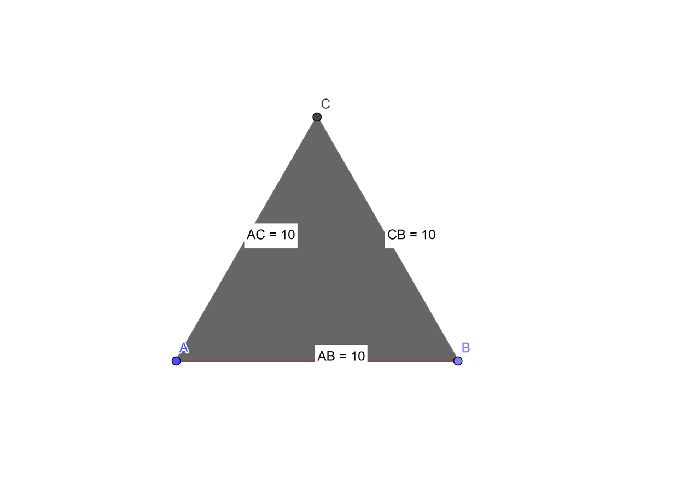
Равносторонний треугольник является равнобедренным, но основанием можно считать любую часть треугольника.

Формула

Формулу высоты равностороннего треугольника выведем тремя способами: через теорему Пифагора, с помощью формулы площади прямоугольного треугольника и через тригонометрическую функцию. Три способа используем, чтобы показать несколько вариантов доказательства и иметь возможность максимально быстро найти значение высоты при любом условии задачи.

Сначала выведем формулу через площадь.

В классической формуле, подходящей для любого треугольника, площадь равна половине произведения основания на высоту. Существует также формула площади для правильного треугольника: $S=\sqrt<3>*$

Приравняем две формулы и выведем формулу высоты.

$<1\over2>*a*h=\sqrt<3>* $ – сократим обе части на а.

$H=\sqrt<3>*$ – и получим формулу высоты равностороннего треугольника.

С другой стороны, в равностороннем треугольнике высота, проведенная к основанию, является медианой и высотой. То есть, высоту можно найти как катет прямоугольного треугольника через теорему Пифагора.

Если в том же малом прямоугольном треугольнике обратить внимание на известный острый угол, то можно вывести значение высоты через синус угла в 60 градусов.

Синус – это отношение противолежащего катета к гипотенузе.

Воспользуемся этим отношением и выразим высоту.

$h=a*sin(60)=\over<2>>$ – как видно, получился тот же результат, что и в первом способе. Это говорит о том, что в равностороннем треугольнике только две формулы высоты, а все остальные способы доказательства можно свести к получившимся выводам.

Что мы узнали?

Мы узнали, что такое равносторонний треугольник, вывели несколько формул для нахождения высоты равностороннего треугольника. Показали несколько путей вывода формул, которые могут помочь быстро вспомнить, как находится высота или использовать те же приемы для нахождения других величин в равностороннем треугольнике.

Источник

Свойства высоты равностороннего треугольника

В данной публикации мы рассмотрим основные свойства высоты в равностороннем (правильном) треугольнике. Также разберем пример решения задачи по этой теме.

Примечание: треугольник называется равносторонним, если все его стороны равны.

Свойства высоты в равностороннем треугольнике

Свойство 1

Любая высота в равностороннем треугольнике одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.

• BD – высота, опущенная на сторону AC;
• BD – медиана, которая делит сторону AC пополам, т.е. AD = DC;
• BD – биссектриса угла ABC, т.е. ∠ABD = ∠CBD;
• BD – серединный перпендикуляр, проведенный к AC.

Свойство 2

Все три высоты в равностороннем треугольнике имеют одинаковую длину.

Свойство 3

Высоты в равностороннем треугольнике в ортоцентре (точке пересечения) делятся в отношении 2:1, считая от вершины, из которой они проведены.

Свойство 4

Ортоцентр равностороннего треугольника является центром вписанной и описанной окружностей.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r (следует из Свойства 3).

Свойство 5

Высота в равностороннем треугольнике делит его на два равных по площади (равновеликих) прямоугольных треугольника.

Три высоты в равностороннем треугольнике делят его на 6 равных по площади прямоугольных треугольников.

Свойство 6

Зная длину стороны равностороннего треугольника его высоту можно вычислить по формуле:

a – сторона треугольника.

Пример задачи

Радиус окружности, описанной вокруг равностороннего треугольника, равняется 7 см. Найдите сторону этого треугольника.

Решение
Как мы знаем из Свойств 3 и 4, радиус описанной окружности составляет 2/3 от высоты равностороннего треугольника (h). Следовательно, h = 7 ∶ 2 ⋅ 3 = 10,5 см.

Теперь остается вычислить длину стороны треугольника (выражение выведено из формулы в Свойстве 6):

Источник

Формулы для нахождения высоты треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты h_a, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

Источник

Все формулы для треугольника

9. Найти медиану биссектрису высоту равностороннего треугольника

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L — высота=биссектриса=медиана

a — сторона треугольника

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, ( L ):

10. Найти длину медианы треугольника по формулам

Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M — медиана, отрезок |AO|

c — сторона на которую ложится медиана

a, b — стороны треугольника

γ — угол CAB

Формула длины медианы через три стороны, ( M ):

Формула длины медианы через две стороны и угол между ними, ( M ):

Источник