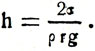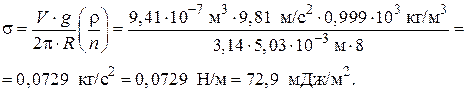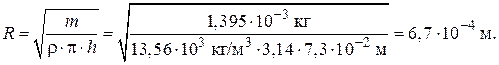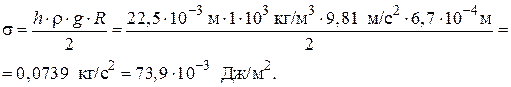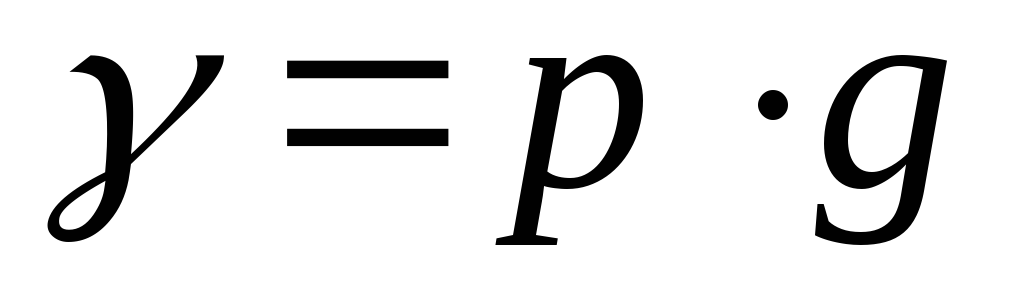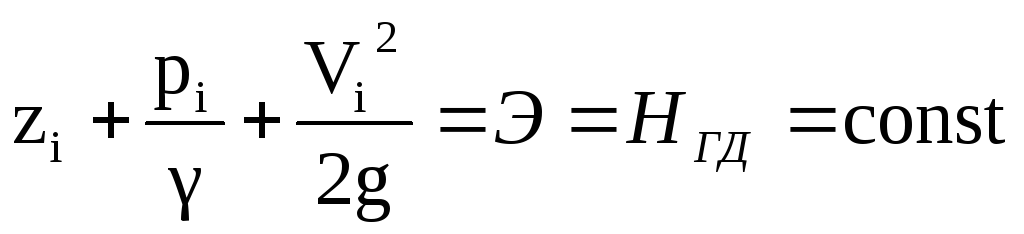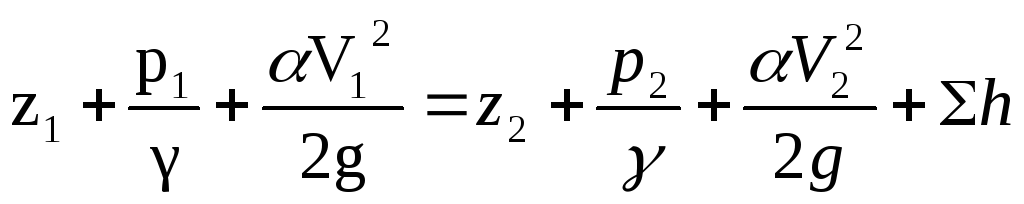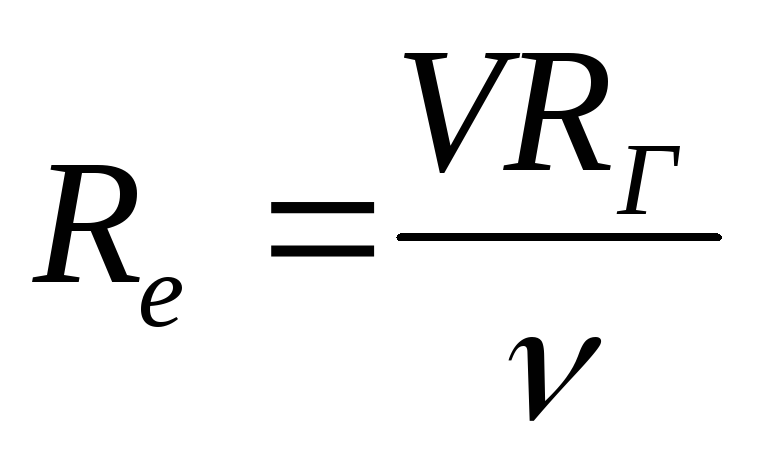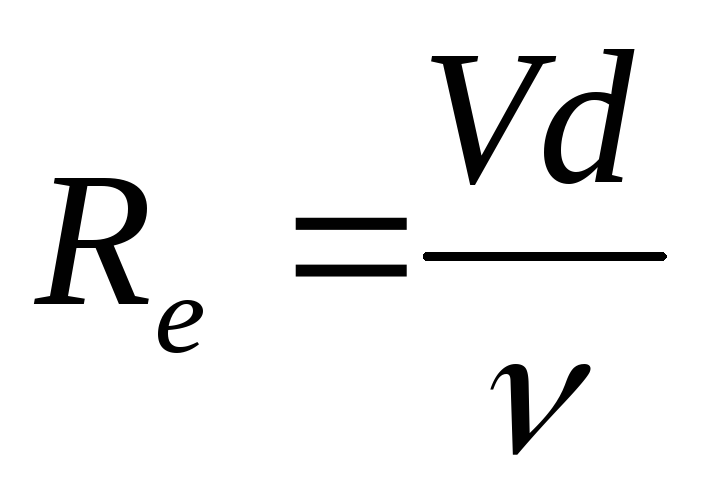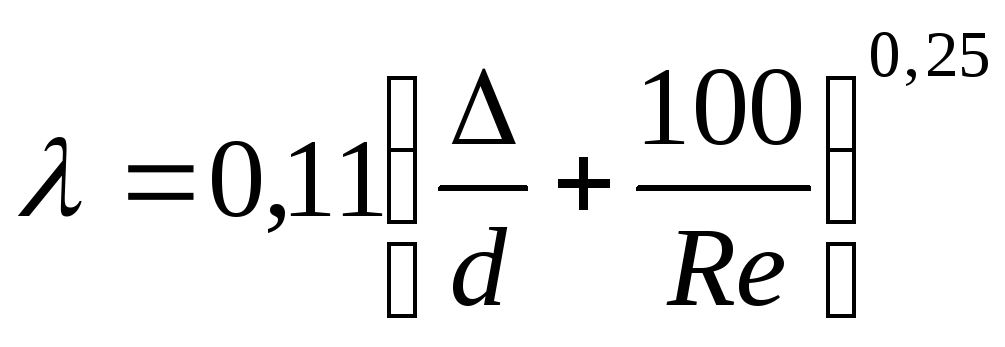Вывести формулу высоты подъема жидкости
§ 19. Капиллярные явления
Продолжим изучение явлений, которые объясняются поверхностным натяжением и смачиванием жидкости.
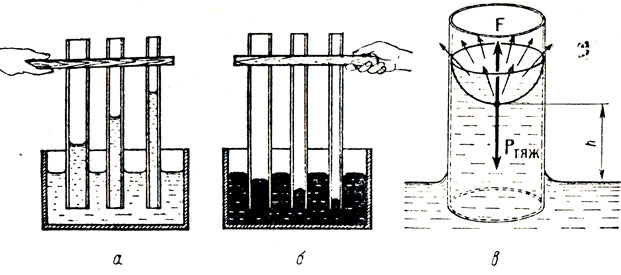
Возьмем капиллярные трубки различного сечения и опустим их сначала в воду, которая смачивает стекло, а затем в ртуть, которая его не смачивает. Вода в капиллярной трубке поднимется (рис. 20, а), а ртуть — опустится (рис. 20, б); при этом высота подъема смачивающей жидкости и опускания несмачивающей тем больше, чем меньше радиус трубки. Погрузим одну из капиллярных трубок с одинаковыми радиусами в воду, другую — в керосин. Видим, что вода поднялась выше, чем керосин. Значит, высота подъема жидкости (а в случае несмачивания — опускания) в капиллярных трубках зависит от рода жидкости. Явление поднятия или опускания жидкости в капиллярах называется капиллярностью. Выясним, почему смачивающая жидкость в капиллярах поднимается, а несмачивающая — опускается.
Рис. 20. Жидкости в капиллярах
Мы знаем, что под действием сил поверхностного натяжения поверхность жидкости стремится сократиться. Вследствие этого поверхность вогнутого мениска стремится выпрямиться и сделаться плоской (рис. 20, в). При этом она тянет за собой частицы жидкости, лежащие под ней, и жидкость поднимается по капилляру вверх. Но поверхность жидкости в узкой трубке плоской оставаться не может, она должна иметь форму вогнутого мениска. Как только в новом положении данная поверхность примет форму мениска, она снова будет стремиться сократиться и т. д. В результате действия этих двух причин смачивающая жидкость и поднимается по капилляру. Поднятие прекратится, когда сила тяжести Ртяж поднятого столба жидкости, которая тянет поверхность вниз, уравновесит равнодействующую силу F сил поверхностного натяжения, изображенных маленькими векторами и направленных касательно к каждой точке поверхности.
По окружности соприкосновения поверхности жидкости со стенкой капилляра действует сила поверхностного натяжения, равная произведению коэффициента поверхностного натяжения σ на длину 2πr окружности: F = σ2πr, где r — радиус капилляра.
Сила тяжести, действующая на поднятую жидкость,
где ρ — плотность жидкости; h — высота столба жидкости в капилляре; g — ускорение силы тяжести.
Подъем жидкости прекращается, когда Ртяж = F или ρπr 2 hg = σ2πr. Отсюда высота поднятия жидкости в капилляре
В случае несмачивающей жидкости последняя, стремясь сократить свою поверхность, будет опускаться вниз, выталкивая жидкость из капилляра. Выведенная формула применима и для несмачивающей жидкости. В этом случае h — высота опускания жидкости в капилляре.
Высота поднятия в капиллярах смачивающей жидкости и опускания несмачивающей обратно пропорциональна радиусу капилляра и плотности жидкости.
В почве имеются капилляры, которые тем уже, чем плотнее почва. По этим капиллярам воду из подпочвенных слоев поднимается до поверхности земли(в песчаной почве с глубины до 30 см, а в суглинистых — до 3 м) и быстро испаряется. Если поверхностный слой почвы вспахать и разрыхлить, разрушив тем самым капилляры, то вода будет подниматься до вспаханного слоя и здесь задерживаться. Проникновение почвенной воды по капиллярам кирпича вызывает сырость в помещениях. Для предотвращения этого между фундаментом дома и стеной прокладывают битум, толь. Эти вещества не имеют капилляров и не смачиваются водой, поэтому вода, поднявшись по порам фундамента, дальше не пойдет. Подъем питательных соков от корня до верхушек растений происходит также по капиллярам.
Источник
Метод капиллярного поднятия жидкости
Высоту капиллярного поднятия (опускания) жидкости в капилляре рассчитывают по уравнению Жюрена (2.30).
На практике краевой угол смачивания 
часто не известен. В этом случае принимают, что жидкость полностью смачивает стенки капилляра (полное смачивание), следовательно, θ = 0°, cosθ= 1, тогда уравнение Жюрена приобретает вид:
. (2.34)
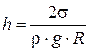
В таком виде уравнение Жюрена используют в практических расчетах для вычисления поверхностного натяжения жидкостей методом поднятия жидкости в капилляре. Отсюда поверхностное натяжение будет равно:
. (2.35)
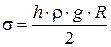
Пример 2.4.Вычислите поверхностное натяжение анилина при 292 К, если методом наибольшего давления пузырька газа получены следующие данные: давление пузырька при проскакивании его в воду 11,82·10 2 Н/м 2 , а в анилин 7,12·10 2 Н/м 2 . Поверхностное натяжение воды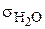 
= 72,55·10 –3 Н/м.
Решение. Поверхностное натяжение анилина рассчитываем по уравнению (2.30):
.
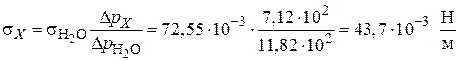
Пример 2.5.Вычислите поверхностное натяжение воды при 17 °С методом счета капель, если диаметр капилляра 5,03 мм, а 8 капель воды имеют объем 0,941 мл. Плотность воды 0,999 г/мл. Полученную величину сравните с табличной (73,1 мДж/м 2 ). Сделайте вывод о степени точности данного метода.
Решение. Вычислим поверхностное натяжение методом счета капель по уравнению (2.31):
Полученное значение поверхностного натяжение воды практически совпадает с табличным, что говорит о высокой точности данного метода.
Пример 2.6.Вычислите поверхностное натяжение воды по методу поднятия в жидкости в капилляре, если при опускании капилляра в воду она поднялась на 22,5 мм. Радиус капилляра был предварительно определен по длине и весу столбика ртути, затянутой в капилляр на высоту 7,3 см. Масса ртути 1,395 г, плотность ртути 13,56·10 3 кг/м 3 .
1. Найдем радиус капилляра. Объем капилляра (цилиндра) равен:
.
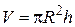
С другой стороны
,
.
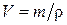
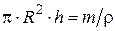
Отсюда находим радиус капилляра:
2. Вычислим поверхностное натяжение воды по уравнению (2.35):
2.7. Влияние кривизны поверхности
на давление насыщенного пара
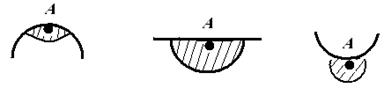
Кривизна поверхности оказывает влияние на давление насыщенного пара. Рассмотрим влияние на молекулу А других (соседних с ней) молекул на плоской, вогнутой и выпуклой поверхности:
Рис. 2.13 Влияние кривизны поверхности на давление насыщенного пара
На выпуклой поверхности воздействие соседних молекул на молекулу А меньше, чем на плоской, поэтому переход молекул из жидкого состояния в газообразное на выпуклой поверхности происходит легче. Число молекул, необходимое для насыщения достигается при меньшем давлении, поэтому давление насыщенного пара над выпуклой поверхностью всегда больше давления насыщенного пара над плоской поверхностью:
.
На вогнутой поверхности воздействие соседних молекул на молекулу А больше, чем на плоской, поэтому переход молекул из жидкого состояния в газообразное на вогнутой поверхности происходит труднее. Число молекул, необходимое для насыщения достигается при большем давлении, поэтому давление насыщенного пара над вогнутой поверхностью всегда меньше давления насыщенного пара над плоской поверхностью:
.
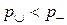
Источник
Формулы гидравлики
(кг/м 3 ) – плотность
(н/м 3 ) – удельный вес
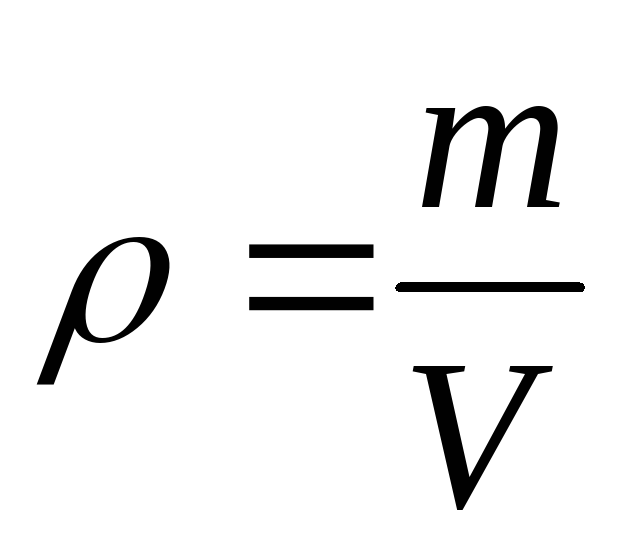
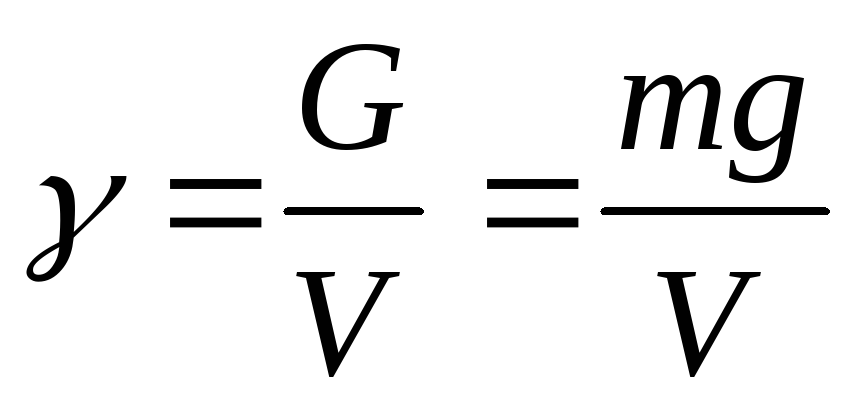
р — давление или сжимающие напряжение (н/м 2 = Па)
Давление всегда направлено к поверхности по внутренней нормали.
Действует одинаково по всем направлениям (не зависит от угла наклона площадки)
Основное уравнение гидростатики:
ро – давление действующее на поверхность жидкости;
рв – весовое давление, т.е. давление столба жидкости.
h – глубина расположения точки;
γ – удельный вес жидкости.
При атмосферном давлении на поверхности:
Закон Паскаля. Давление действующее на поверхность жидкости передается во все ее точки без изменения.
Любая горизонтальная плоскость проведенная в жидкости, является плоскостью равного давления.
Можем измерять величину давления эквивалентной ему высотой столба жидкости.
Например давление величиной в 1 атм. р = 1 кгс/см 2 соответствует
h = 10 м вод. столба
Сила давления жидкости на плоскую поверхность
рс = hсγ – давление в центре тяжести при атмосферном давлении на поверхности
hс – глубина расположения центра тяжести поверхности (м);
S – площадь поверхности (м 2 ).
Потенциальная энергия покоящейся жидкости величина постоянная, т.е. одинаковая для всех точек жидкости
Удельная энергия (напор) Э = Е/G = Е/mg (м)
Z – геометрический напор;
НГС –гидростатический напор или полная удельная потенциальная энергия жидкости.
Q – расход жидкости (м 3 /с);
V – средняя скорость потока (м/с);
Ω – площадь живого сечения потока (м 2 ).
Уравнение Бернулли для идеальной жидкости (при действии сил давления и сил тяжести)
где z — геометрический напор, м;
P/γ — приведенная пьезометрическая высота (если Р — абсолютное давление) или пьезометрическая высота (если Р — избыточное давление), м;
— гидростатический напор,
удельная потенциальная энергия жидкости
НГС = Э – гидродинамический напор или полная удельная энергия
Уравнение Бернулли для реальной жидкости (с учетом сил трения (вязкости)).
α= ЕКД /ЕКУ – коэффициент кинетический энергии (коэффициент Кориолиса);
(м)
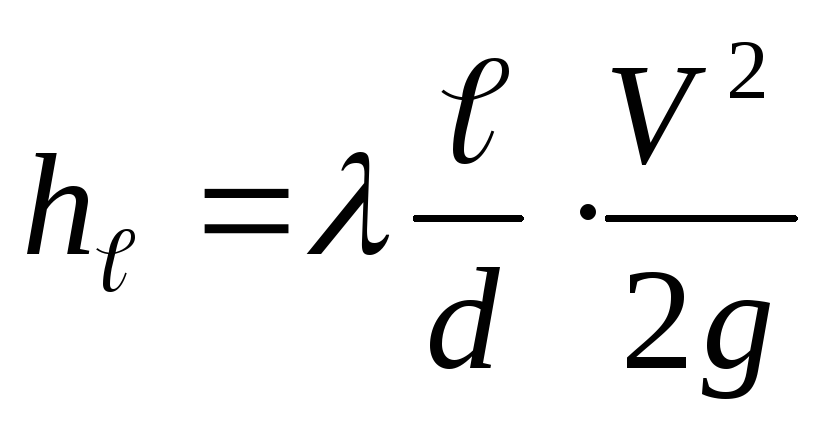
hм – потери на местных сопротивлениях.
(м)
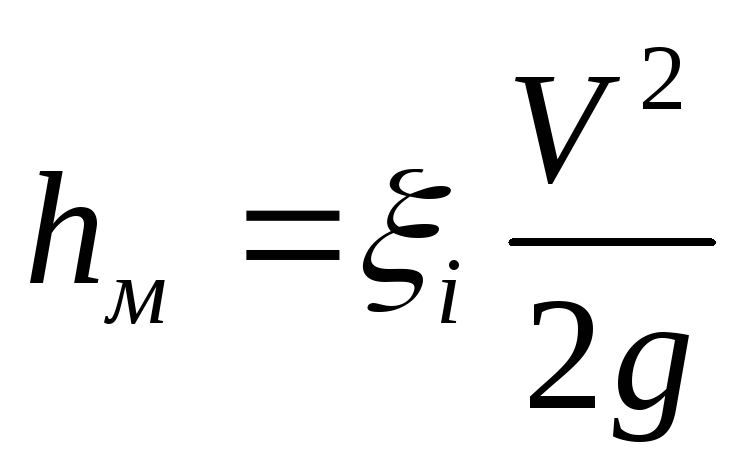
Число (критерий) Рейнольдса 
Для кругло-цилиндрических труб 
(м)
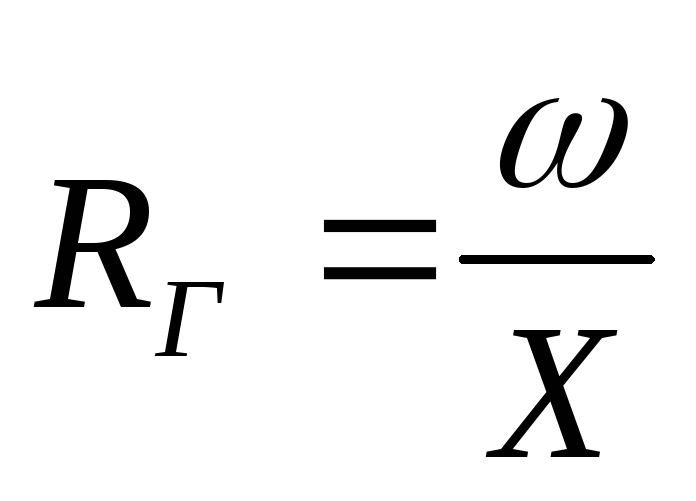
ω – площадь живого сечения потока (м 2 );
Х – смоченный периметр.
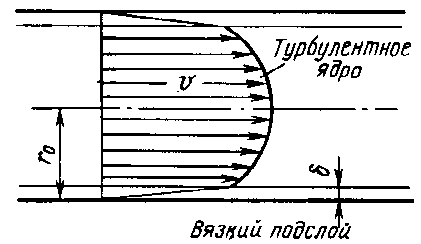
Профиль скорости при турбулентном движении
Толщина ламинарной пленки δ уменьшается с увеличением скорости V (числа Рейнольдса)
В турбулентном режиме имеется три вида трения:
Гидравлически гладкие русла
Шероховатое трение, квадратичная область турбулентного режима
СКОРОСТЬ ДВИЖЕНИЯ (ИСТЕЧЕНИЯ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
(м/с)
— коэффициент скорости
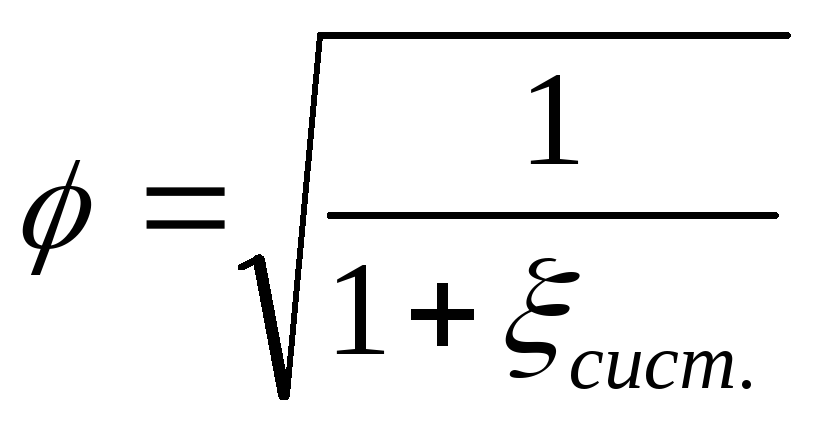
Но – действующий (расчетный напор (м)
(м 3 /с)
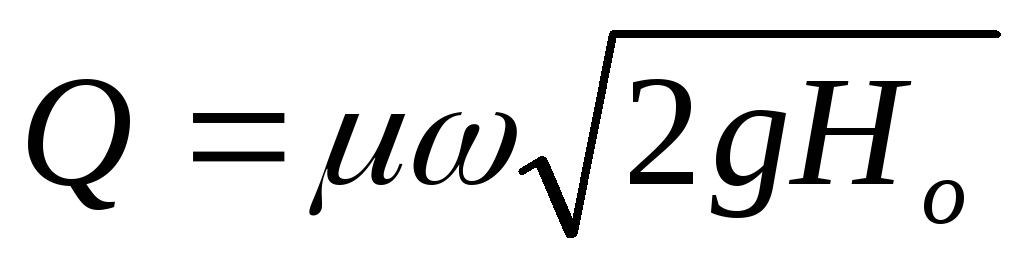
μ = φε – коэффициент расхода;
ω – площадь проходного (живого) сечения потока (м 2 );
Источник
