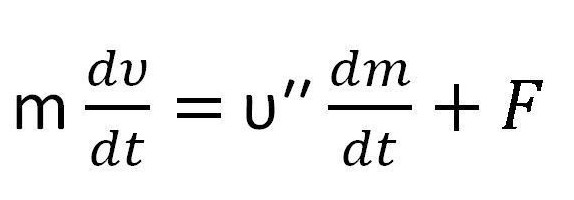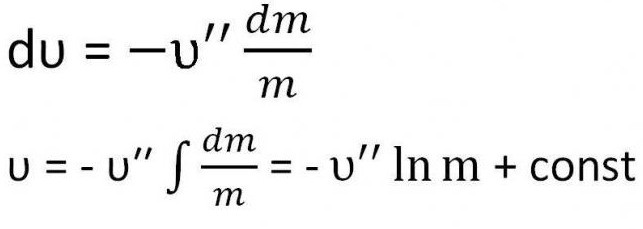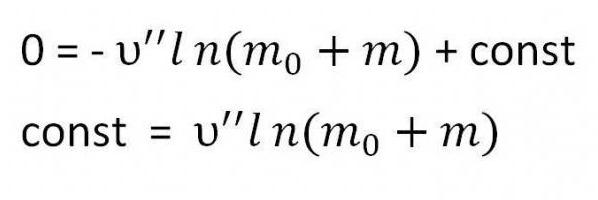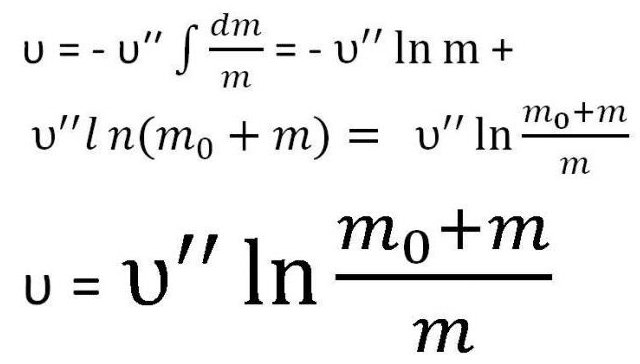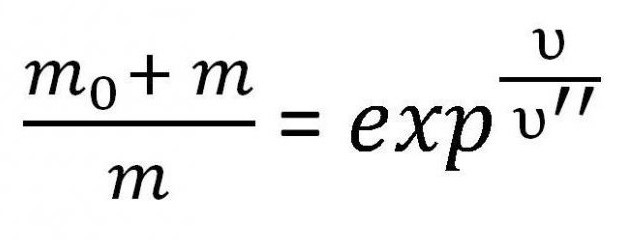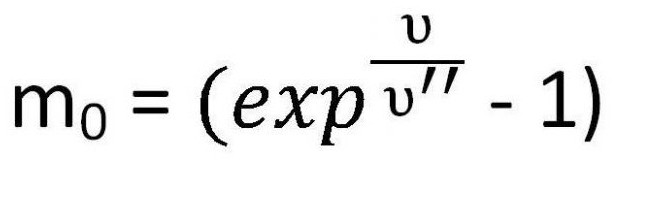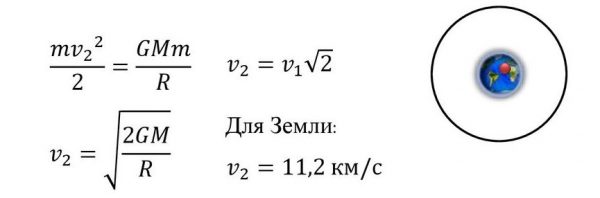Вывести формулу скорости ракеты

Вывод формулы скорости ракеты при взлете

Скачать
презентацию Двухступенчатая космическая ракета >>

Вывод формулы скорости ракеты при взлете. Согласно третьему закону Ньютона: где – сила, с которой ракета действует на раскаленные газы – сила, с которой газы отталкивают от себя ракету. Именно сила является реактивной силой. Рассчитаем скорость, которую может приобрести ракета. Если импульс выброшенных газов равен , а импульс ракеты , то по закону сохранения импульса, получаем: Откуда скорость ракеты:

Слайд 9 из презентации «Реактивный способ движения». Размер архива с презентацией 2298 КБ.

Физика 9 класс

«Закон тяготения Ньютона» — И. Ньютон — профессор. Два любых тела притягиваются друг к другу. Самолюбивый Ньютон. Закон неприменим. 1667 год. Украшение человеческого рода. Вершина славы. G – гравитационная постоянная. Как долго он формулировал свои законы. Немного юмора. Биография И. Ньютона. Закон применим. Законы И. Ньютона. Поколение новых яблонь. И. Ньютон — студент. Закон всемирного тяготения. Все тела во Вселенной взаимно притягивают друг друга.

«Применение ядерной энергетики» — Рентген. Ядерное оружие. Радиоактивные изотопы. Применение ядерной энергии. Защита организмов от излучения. Ядерные реакторы. Мощное излучение. Преимущества АЭС. Получение радиоактивных изотопов. Способ контроля износа деталей. Биологическое действие радиоактивных излучений. Облучение семян. Эквивалентная доза. Потенциальная угроза. Развитие ядерной энергетики. Что такое доза излучения. Доза излучения.

««Скорость распространения звука» 9 класс» — Объясните, как слуга из рассказа «Барон Мюнхаузен» смог узнать, что скороход заснул. Знаешь ли ты. Самый маленький микрофон. Самое тихое место. Как зависит скорость звука от среды. Скорость звука. Установки, создающие комфортный легкий шум. Распространение звука. Как бороться с шумом. Может ли звук распространяться в газах.

«Распространение звуковых волн» — Вопрос. Звук имеет определённую скорость. Музыка и шум. Два основных аспекта. Звук. Что такое звук. Предсказуемое явление. Звук обладает свойством огибать препятствия. Источники звука. Обсуждение плана работы. Звуковые волны. Знания о звуке. С помощью речи люди общаются. Передача звука. Колебания окружающей среды. Звуковая волна. Мир звуков. Механические упругие волны. Лёгкие газы. Звук является средством обмена информацией.

«Первая космическая скорость» — Условия, при которых тело становится ИСЗ. Решите задачу. Искусственные спутники Земли. Ускорение свободного падении. Первая космическая скорость. Представление об ИСЗ. Решите задачи. Определить первую космическую скорость для запуска спутника. Обращение планет вокруг Солнца. Скорость, которую необходимо сообщить телу, чтобы оно стало спутником.

«Творчество и учёные» — Художник Михаил Федорович Ларионов. Выдающиеся ученые. Русский художник. Симметрия . Фрактал. Эйнштейн. Музыка. Изучение проблем оптического восприятия. Французский физик. Художник и учёный. Голландский художник.

Всего в теме «Физика 9 класс» 93 презентации

Источник

Формула Циолковского: использование и пример

Формула Константина Эдуардовича Циолковского выражает максимальную скорость летательного аппарата, которой он достигает во время полета при реактивном движении. Она получается при интегрировании уравнения Мещерского.

Формула Циолковского

Эта формула выражает скорость ракеты, переданную газами от сожженного топлива. Уравнение Мещерского и формула Циолковского неразрывно связаны — уравнение Мещерского описывает массу материальной точки, которая изменяется со временем, в то время как при реактивном движении ракеты постоянно идет уменьшение ее массы из-за сгорания топлива. Изменение скорости при изменяющейся массе (уменьшающейся в нашем случае) движущегося тела — вот что подразумевает под собой реактивное движение. Формула Циолковского основывается именно на нем.

Для решения ряда задач теоретической механики в области реактивного движения используют уравнение Мещерского (основное уравнение материальной точки переменной массы) и формулу Циолковского (формула конечной скорости летательного аппарата), которые называются основными соотношениям теории реактивного движения.

Основой при проектировании и планировании в области космических полетов является именно формула Циолковского, вывод которой стал настоящим прорывом для освоения космоса.

Задачи Циолковского

Для того, чтобы разрешить проблему межпланетных перелетов, К. Э. Циолковский рассмотрел в качестве средства перелета ракету. Он вывел формулу, с помощью которой можно получить зависимость массы летательного аппарата с топливом и скорости отдаления продуктов сгорания используемого топлива ракеты относительно нее. Покажем две его задачи:

• Исследование движения тела с переменной массы с действующей на него одной реактивной силы.
• Исследование движение тела в однородном поле силы тяжести переменной массы вблизи поверхности Земли.

Предисловие

Для всех космических полетов изначальной и основополагающей стала формула Циолковского для скорости ракеты, вывод которой представлен ниже.

Для начала необходимо приняв ее, грубо говоря, за материальную точку. На нее будут действовать силы притяжения Земли и других небесных тел (в момент взлета сила гравитации Земли будет, конечно же, наиболее сильной), сила сопротивления воздуха с одной стороны и противоположно им направленная реактивная сила, возникающая из-за выброса сгоревшего газа у основания тела. Ракета с большой силой выбрасывает эти газы, которые сообщают ей ускорение, направленное противоположно стороне выброса. Теперь необходимо представить эти рассуждения в виде формулы.

Сам принцип полета ракеты достаточно простой. С большой скоростью из ракеты вырывается газ, полученный при сгорании топлива, который сообщает самой ракете определенную силу, которая действует противоположно направлению движения. Так как считается, что внешние силы не действуют на ракету, то система будет замкнутой, и импульс ее не зависит от времени.

Уравнение Мещерского

Одним из основных примеров движения тела с изменяющейся массой является ракета с одной ступень, масса которой изменяется только из-за сжигания топлива, содержащегося в ней. Масса такой ракеты складывается из неизменяющейся (сама ракета и ее полезная нагрузка) и изменяющейся (топливо). Такой пример является упрощенной моделью.

Однако в современном ракетостроении используются многоступенчатые ракеты. Принцип их работы заключается в том, что благодаря большому объему ступеней они способны перевозить и использовать после взлета гораздо большее количество топлива. После его сгорания, ракете сообщается значительный импульс (гораздо больший, чем тот, которого можно добиться, используя одну ступень), а ставшие ненужными части открепляются от основы, уменьшая общий вес на 80-90%. Тем не менее, для расчета параметров многоступенчатой ракеты необходимо сложить показатели каждой из ее составляющей.

Дифференциальное уравнение Мещерского описывает движение материальной точки с переменной массой.

(m+dm)(υ+dυ) + dm′ υ′ — mυ = Fdt — в момент времени dt (разность между силой в момент времени t и dt+t и будет приращением).

Где m и υ зависят от времени, dt — какое-то время полета. За его образуется сила перемещения газа — dm′ υ′, dm′ — масса образованного из топлива газа. F — равнодействующая сила.

В описанном выше выражении приращения массы ракеты и газа и скорости устремляется к нулю, поэтому выражение принимает следующий вид:

причем υ′′ равняется разности скорости газа и скорости и является скоростью истечения газа.

Оно и называется уравнением Мещерского.

Вывод формулы Циолковского

Необходимо вывести формулу, описывающую движение тела с переменной массой. Формула Циолковского таковой и является. Вывод представлен ниже.

В данных вычислениях считается, что на движущееся тело не действуют внешние силы, то есть F = 0.

Так как воздействие внешних сил на летящую ракету равно нулю, то она движется прямолинейно, а скорость движения противоположно направлена скорости выхода газа. Соответственно, υ = -υ′′

Получается выражение, которое необходимо проинтегрировать.

Необходимо найти константу. Для этого достаточно подставить в уравнение начальные условия — скорость равна нулю, а масса — сумме массы топлива и массы ракеты (m₀ + m)

Вообще говоря, m в формуле складывается из двух параметров — из полезной нагрузки и конструкции ракеты. Полезной нагрузкой называется общая масса груза и экипажа.

Подставляем найденную константу в формулу. В результате и получается выражение искомой формулы.

Это и есть один из вариантов формулы Циолковского для скорости. Однако иногда необходимо принять во внимание именно массу. Поэтому ее иногда записывают следующим образом:

Данная формула используется для расчета массы топлива, которая требуется для развития определенной скорости при заданных условиях.

Рассмотрю далее небольшую задачу. Предположим, ракете необходимо развить первую космическую скорость для вращения по орбите Земли. Тогда для этого необходимо в первую очередь рассчитать массу топлива, конечно же. Тогда ее очень просто выразить из формулы Циолковского.

Релятивистская механика

Все вышеописанные формулы могут применяться только в том случае, когда скорость ракеты много меньше скорости света (υ

Источник

Космические скорости

Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?

На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.

Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.

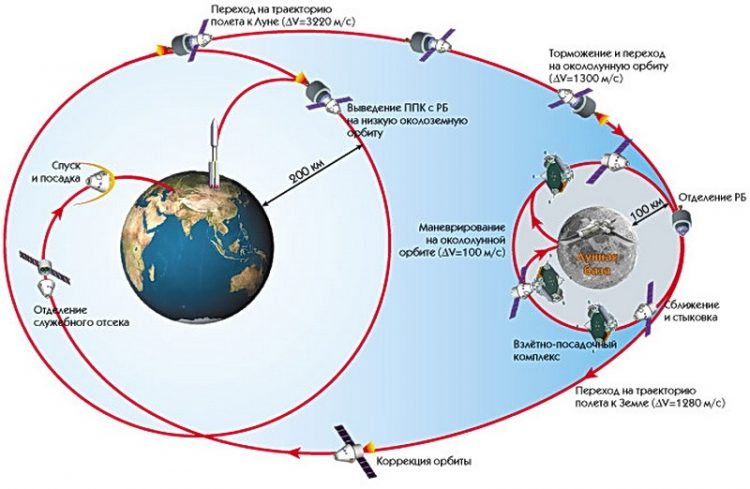
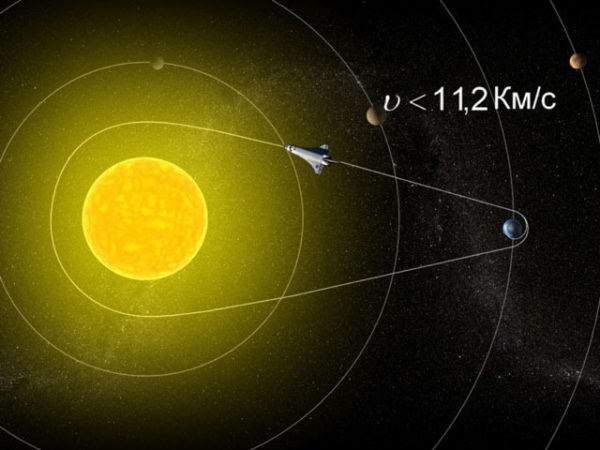
Траектория полета космических кораблей

Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.

Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.

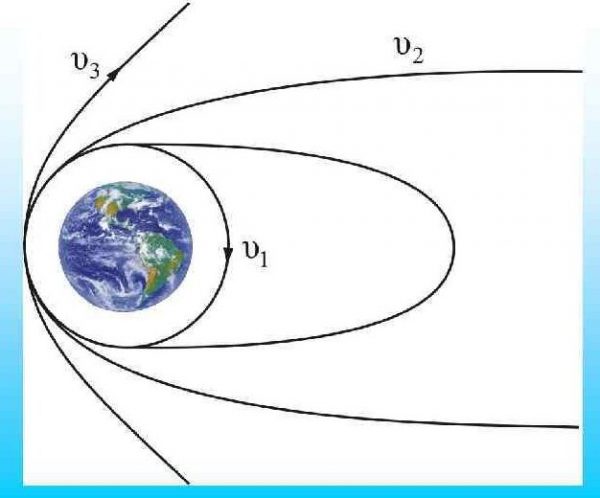
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:

• v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг небесного тела и не падать на его поверхность);
• v2 — преодолеть гравитационное притяжение небесного тела и начать двигаться по параболической орбите;
• v3 — покинуть при запуске планету, преодолев притяжение Звезды;
• v4 — при запуске из планетной системы объект покинул Галактику.

Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.

Первая космическая скорость

Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.

Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.

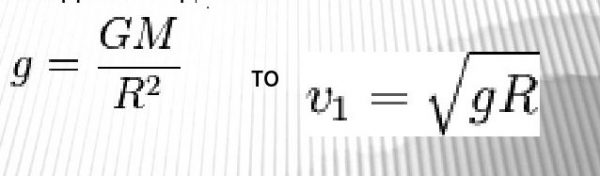
Формула

где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем

7,9 км/с

Первую космическую скорость можно определить через ускорение свободного падения —

Вторая космическая скорость

Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.

Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).

Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:

• для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца.
• для Солнца вторая космическая скорость составляет 617,7 км/с.
• для Луны скорость убегания равна 2,4 км/с , несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.

Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.

Формула

Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .

Третья космическая скорость

Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.

Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.

Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.

Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.

При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.

Четвёртая и пятая космическая скорости

Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.

Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.

Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.

По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.

Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.

Видео

Источник