Вывести формулу синус двойного угла формулы

Тригонометрические формулы: косинус, синус и тангенс двойного угла

Формулы двойного угла дают возможность выразить тригонометрические функции (синус, косинус, тангенс, котангенс) угла ` 2\alpha` через эти самые функции угла `\alpha`.

Перечень всех формул двойного угла

Записанный ниже список — это основные формулы двойного угла, которые наиболее часто используются в тригонометрии. Для косинуса их есть три, они все равносильны и одинаково важны.

`sin \ 2\alpha=` `2 \ sin \ \alpha \ cos \ \alpha`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha`, ` cos \ 2\alpha=1-2 \ sin^2 \alpha`, `cos \ 2\alpha=2 \ cos^2 \alpha-1`
`tg \ 2\alpha=\frac<2 \ tg \alpha><1-tg^2 \alpha>`
`ctg \ 2\alpha=\frac<2 \ ctg \alpha>`

Следующие тождества выражают все тригонометрические функции угла ` 2\alpha` через функции тангенс и котангенс угла `\alpha`.

Формулы для косинуса и синуса двойного угла выполняются для любого угла `\alpha`. Формулы для тангенса двойного угла справедливы для тех `\alpha`, при которых определен `tg \ 2\alpha`, то есть при ` \alpha\ne\frac\pi4+\frac\pi2 n, \ n \in Z`. Аналогично, для котангенса они имеют место для тех `\alpha`, при которых определен `ctg \ 2\alpha`, то есть при ` \alpha\ne\frac\pi2 n, \ n \in Z`.

Доказательство формул двойного угла

Все формулы двойного угла выводятся из формул сумы и разности углов тригонометрических функций.

Возьмем две формулы, для сумы углов синуса и косинуса:

`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta` и `cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`. Возьмем `\beta=\alpha`, тогда `sin(\alpha+\alpha)=` `sin \ \alpha\ cos \ \alpha+cos \ \alpha\ sin \ \alpha=2 \ sin \ \alpha \ cos \ \alpha`, аналогично `cos(\alpha+\alpha)=` `cos \ \alpha\ cos \ \alpha-sin \ \alpha\ sin \ \alpha=cos^2 \alpha-sin^2 \alpha`, что и доказывает формулы двойного угла для синуса и косинуса.

Два другие равенства для косинуса ` cos \ 2\alpha=1-2 \ sin^2 \alpha` и `cos \ 2\alpha=2 \ cos^2 \alpha-1` сводятся к уже доказанному, если в них заменить 1 на `sin^2 \alpha+cos^2 \alpha=1`. Так `1-2 \ sin^2 \alpha=` `sin^2 \alpha+cos^2 \alpha-2 \ sin^2 \alpha=` `cos^2 \alpha-sin^2 \alpha` и `2 \ cos^2 \alpha-1=` `2 \ cos^2 \alpha-(sin^2 \alpha+cos^2 \alpha)=` `cos^2 \alpha-sin^2 \alpha`.

Чтобы доказать формулы тангенса двойного угла и котангенса, воспользуемся определением этих функций. Запишем `tg \ 2\alpha` и `ctg \ 2\alpha` в виде `tg \ 2\alpha=\frac ` и `ctg \ 2\alpha=\frac `. Применив уже доказанные формулы двойного угла для синуса и косинуса, получим `tg \ 2\alpha=\frac =\frac <2 \ sin \alpha cos>` и `ctg \ 2\alpha=\frac =` `\frac <2 \ sin \alpha cos>`.

В случае с тангенсом разделим числитель и знаменатель конечной дроби на `cos^2 \alpha`, для котангенса в свою очередь — на `sin^2 \alpha`.

Предлагаем еще посмотреть видео, чтобы лучше закрепить теоретический материал:

Примеры использования формул при решении задач

Формулы двойного угла в большинстве случаев используются для преобразование тригонометрических выражений. Рассмотрим некоторые из случаем, как можно на практике применять их при решений конкретных задач.

Пример 1. Проверить справедливость тождеств двойного угла для `\alpha=30^\circ`.

Решение. В наших формулах используется два угла `\alpha` и `2\alpha`. Значение первого угла задано в условии, второго соответственно будет `2\alpha=60^\circ`. Также нам известны числовые значения для всех тригонометрических функций этих углов. Запишем их:

`sin 30^\circ=\frac 1 2`, `cos 30^\circ=\frac <\sqrt 3>2`, `tg 30^\circ=\frac <\sqrt 3>3`, `ctg 30^\circ=\sqrt 3` и

`sin 60^\circ=\frac <\sqrt 3>2`, `cos 60^\circ=\frac 1 2`, `tg 60^\circ=\sqrt 3`, `ctg 60^\circ=\frac <\sqrt 3>3`.

Тогда будем иметь

`sin 60^\circ=2 sin 30^\circ cos 30^\circ=` `2 \cdot \frac 1 2 \cdot \frac <\sqrt 3>2=\frac <\sqrt 3>2`,

`cos 60^\circ=cos^2 30^\circ-sin^2 30^\circ=` `(\frac <\sqrt 3>2)^2 \cdot (\frac 1 2)^2=\frac 1 2`,

Что и доказывает справедливость равенств для заданного в условии угла.

Пример 2. Выразить `sin \frac <2\alpha>3` через тригонометрические функции угла `\frac <\alpha>6`.

Решение. Запишем угол синуса следующим образом ` \frac <2\alpha>3=4 \cdot \frac <\alpha>6`. Тогда, применив два раза формулы двойного угла, мы сможем решить нашу задачу.

Вначале воспользуемся равенством синуса двойного угла: ` sin\frac <2\alpha>3=2 \cdot sin\frac <\alpha>3 \cdot cos\frac <\alpha>3 `, теперь снова применим наши формулы для синуса и косинуса соответственно. В результате получим:

` sin\frac <2\alpha>3=2 \cdot sin\frac <\alpha>3 \cdot cos\frac <\alpha>3=` `2 \cdot (2 \cdot sin\frac <\alpha>6 \cdot cos\frac <\alpha>6) \cdot (cos^2\frac <\alpha>6-sin^2\frac <\alpha>6)=` `4 \cdot sin\frac <\alpha>6 \cdot cos^3 \frac <\alpha>6-4 \cdot sin^3\frac <\alpha>6 \cdot cos \frac <\alpha>6`.

Ответ. ` sin\frac <2\alpha>3=` `4 \cdot sin\frac <\alpha>6 \cdot cos^3 \frac <\alpha>6-4 \cdot sin^3\frac <\alpha>6 \cdot cos \frac <\alpha>6`.

Формулы тройного угла

Эти формулы, аналогично к предыдущим, дают возможность выразить функции угла ` 3\alpha` через эти самые функции угла `\alpha`.

Доказать их можно, используя равенства сумы и разности углов, а также хорошо известные нам формулы двойного угла.

`sin \ 3\alpha= sin (2\alpha+ \alpha)=` `sin 2\alpha cos \alpha+cos 2\alpha sin \alpha=` `2 sin \alpha cos \alpha cos \alpha+(cos^2 \alpha-sin^2 \alpha) sin \alpha=` `3 sin \alpha cos^2 \alpha-sin^3 \alpha`.

Заменим в полученной формуле `sin \ 3\alpha=3 sin \alpha cos^2 \alpha-sin^3 \alpha` `cos^2\alpha` на `1-sin^2\alpha` и получим `sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`.

Также и для косинуса тройного угла:

`cos \ 3\alpha= cos (2\alpha+ \alpha)=` `cos 2\alpha cos \alpha-sin 2\alpha sin \alpha=` `(cos^2 \alpha-sin^2 \alpha) cos \alpha-2 sin \alpha cos \alpha sin \alpha+=` `cos^3 \alpha-3 sin^2 \alpha cos \alpha`.

Заменив в конечном равенстве `cos \ 3\alpha=cos^3 \alpha-3 sin^2 \alpha cos \alpha` `sin^2\alpha` на `1-cos^2\alpha`, получим `cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`.

С помощью доказанных тождеств для синуса и косинуса можно доказать для тангенса и котангенса:

Для доказательства формул угла ` 4\alpha` можно представить его как ` 2 \cdot 2\alpha` и примерить два раза формулы двойного угла.

Для вывода аналогичных равенств для угла ` 5\alpha` можно записать его, как ` 3\alpha + 2\alpha` и применить тождества суммы и разности углов и двойного и тройного угла.

Аналогично выводятся все формулы для других кратных углов, то нужны они на практике крайне редко.

Источник

Формулы двойного угла в тригонометрии

Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.

Список формул двойного угла

Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin ( n α ) . При обозначении sin n α имеем аналогичную запись ( sin α ) n . Использование записи применимо для всех тригонометрических функций со степенями n .

Ниже приведены формулы двойного угла:

sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α

Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .

Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.

Доказательство формул двойного угла

Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:

sin ( α + β ) = sin α · cos β + cos α · sin β и косинуса суммы cos ( α + β ) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что

sin ( α + α ) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos ( α + α ) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α

Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .

Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — ( sin 2 α + cos 2 α ) = cos 2 α — sin 2 α .

Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:

t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α = 2 · sin α · cos α cos 2 α cos 2 α — sin 2 α cos 2 α = 2 · sin 2 α cos 2 α 1 — sin 2 α cos 2 α = 2 · t g α 1 — t g 2 α c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos = cos 2 α — sin 2 α sin 2 α 2 · sin α · cos α sin 2 α = cos 2 α sin 2 α — 1 2 · cos α sin α = c t g 2 α — 1 2 · c t g α

Примеры использования формул двойного угла

Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2 α для α = 30 ° , применим значения тригонометрических функций для этих углов. Если α = 30 ° , тогда 2 α = 60 ° . Проверим значения sin 60 ° = 2 · sin 30 ° · cos 30 ° , cos 60 ° = cos 2 30 ° — sin 2 30 ° .

Подставив значения, получим t g 60 ° = 2 · t g 30 ° 1 — t g 2 30 ° и c t g 60 ° = c t g 2 30 ° — 1 2 · c t g 30 ° . .

Известно, что sin 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 и

sin 60 ° = 3 2 , cos 60 ° = 1 2 , t g 60 ° = 3 , c t g 60 ° = 3 3 , тогда отсюда видим, что

2 · sin 30 ° · cos 30 ° = 2 · 1 2 · 3 2 = 3 2 , cos 2 30 ° — sin 2 30 ° = ( 3 2 ) 2 — ( 1 2 ) 2 = 1 2 , 2 · t g 30 ° 1 — t g 2 30 ° = 2 · 3 2 1 — ( 3 3 ) = 3

и c t g 2 30 ° — 1 2 · c t g 30 ° = ( 3 ) 2 — 1 2 · 3 = 3 3

Проведя вычисления, можно сделать вывод, что справедливость для α = 30 ° подтверждена.

Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2 α . В примере допускается применение формулы двойного угла 3 π 5 . Тогда его необходимо преобразовать, в результате чего получим α = 3 π 5 : 2 = 3 π 10 . Отсюда следует, что формула двойного угла для косинуса будет иметь вид cos 3 π 5 = cos 2 3 π 10 — sin 2 3 π 10 .

Представить sin 2 α 3 через тригонометрические функции, при α 6 .

Заметим, что из условия имеем 2 α 3 = 4 · α 6 . Тогда использовав 2 раза формулу двойного угла, выразим sin 2 α 3 через тригонометрические функции угла α 6 . Применяя формулу двойного угла, получим sin 2 α 3 = 2 · sin α 3 · cos α 3 . После чего к функциям sin α 3 и cos α 3 применим формулы двойного угла: sin 2 α 2 = 2 · sin α 3 · cos α 3 = 2 · ( 2 · sin α 5 · cos α 6 ) · ( cos 2 α 6 — sin α 6 ) = = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6

Ответ: sin 2 α 3 = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6 .

Формулы тройного, четверного и т.д. угла

Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.

sin 3 α = sin ( 2 α + α ) = sin 2 α · cos α + cos 2 α · sin α = 2 · sin α · cos α · cos α + ( cos 2 α — sin 2 α ) · sin α = = 3 · sin α · cos 2 α — sin 3 α

При замене cos 2 α на 1 — sin 2 α из формулы sin 3 α = 3 · sin α · cos 2 α — sin 3 α , она будет иметь вид sin 3 α = 3 · sin α — 4 · sin 3 α .

Так же приводится формула косинуса тройного угла:

cos 3 α = cos ( 2 α + α ) = cos 2 α · cos α — sin 2 α · sin α = = ( cos 2 α — sin 2 α ) · cos α — 2 · sin α · cos α · sin α = cos 3 α — 3 · sin 2 α · cos α

При замене sin 2 α на 1 — cos 2 α получим формулу вида cos 3 α = — 3 · cos α + 4 · cos 3 α .

При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:

t g 3 α = sin 3 α cos 3 α = 3 · sin α · cos 2 α — sin 3 α cos 3 α — 3 · sin 2 α · cos α = 3 · sin α · cos 2 α — sin 3 α cos 3 α cos 3 α — 3 · sin 2 α · cos α cos 3 α = = 3 · sin α cos α — sin 3 α cos 3 α 1 — 3 · sin 2 α cos 2 α = 3 · t g α — t g 3 α 1 — 3 · t g 2 α ; c t g 3 α = cos 3 α sin 3 α = cos 3 α — 3 · sin 2 α · cos α 3 · sin α · cos 2 α — sin 3 α = cos 3 α — 3 · sin 2 α · cos α sin 3 α 3 · sin α · cos 2 α — sin 3 α sin 3 α = = cos 3 α sin 3 α — 3 · cos α sin α 3 · cos 2 α sin 2 α — 1 = c t g 3 α — 3 · c t g α 3 · c t g 2 α — 1

Чтобы выводить формулы четвертой степени, имеет смысл представить 4 α как 2 · 2 α , тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5 α в виде 3 α + 2 α , что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.

Источник

Тригонометрические формулы. Их вывод

Наиболее часто встречающиеся тригонометрические формулы:

\(\blacktriangleright\) Основные тождества: \[\begin <|l|l|>\hline \sin^2 \alpha+\cos^2 \alpha =1& \mathrm\, \alpha \cdot \mathrm\, \alpha =1 \\ &(\sin\alpha\ne 0, \cos\alpha\ne 0)\\[0.5ex] \hline &\\ \mathrm\, \alpha=\dfrac<\sin \alpha> <\cos \alpha>&\mathrm\, \alpha =\dfrac<\cos \alpha> <\sin \alpha>\\&\\ 1+\mathrm^2\, \alpha =\dfrac1 <\cos^2 \alpha>& 1+\mathrm^2\, \alpha=\dfrac1<\sin^2 \alpha>\\&\\ (\cos\alpha\ne 0)& (\sin\alpha\ne 0) \\ \hline \end\]

\(\blacktriangleright\) Формулы сложения углов: \[\begin <|l|r|>\hline &\\ \sin<(\alpha\pm \beta)>=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha & \cos<(\alpha\pm \beta)>=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &\\ \hline &\\ \mathrm\, (\alpha\pm \beta)=\dfrac<\mathrm\, \alpha\pm \mathrm\, \beta><1 \mp \mathrm\, \alpha\cdot \mathrm\, \beta> & \mathrm\, (\alpha\pm\beta)=-\dfrac<1\mp \mathrm\, \alpha\cdot \mathrm\, \beta><\mathrm\, \alpha\pm \mathrm\, \beta>\\&\\ \cos\alpha\cos\beta\ne 0&\sin\alpha\sin\beta\ne 0\\ \hline \end\]

\(\blacktriangleright\) Формулы двойного и тройного углов: \[\begin <|lc|cr|>\hline \sin <2\alpha>=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos<2\alpha>=\cos^2\alpha -\sin^2\alpha\\ \sin \alpha\cos \alpha =\dfrac12\sin <2\alpha>&& & \cos<2\alpha>=2\cos^2\alpha -1\\ & & & \cos<2\alpha>=1-2\sin^2 \alpha\\ \hline &&&\\ \mathrm\, 2\alpha = \dfrac<2\mathrm\, \alpha><1-\mathrm^2\, \alpha> && & \mathrm\, 2\alpha = \dfrac<\mathrm^2\, \alpha-1><2\mathrm\, \alpha>\\&&&\\ \cos\alpha\ne 0, \ \cos2\alpha\ne 0 &&& \sin\alpha\ne 0, \ \sin2\alpha\ne 0\\ \hline &&&\\ \sin <3\alpha>=3\sin \alpha -4\sin^3\alpha && & \cos<3\alpha>=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline \end\]

\(\blacktriangleright\) Формулы понижения степени: \[\begin <|lc|cr|>\hline &&&\\ \sin^2\alpha=\dfrac<1-\cos<2\alpha>>2 &&& \cos^2\alpha=\dfrac<1+\cos<2\alpha>>2\\&&&\\ \hline \end\]

\(\blacktriangleright\) Формулы произведения функций: \[\begin <|c|>\hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos<(\alpha-\beta)>-\cos<(\alpha+\beta)>\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos<(\alpha-\beta)>+\cos<(\alpha+\beta)>\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin<(\alpha-\beta)>+\sin<(\alpha+\beta)>\bigg)\\\\ \hline \end\]

\(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin <|l|r|>\hline &\\ \sin<2\alpha>=\dfrac<2\mathrm\, \alpha><1+\mathrm^2\, \alpha> & \cos<2\alpha>=\dfrac<1-\mathrm^2\, \alpha><1+\mathrm^2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]

\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin <|c|>\hline \text<Частный случай>\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin<\left(\alpha\pm \dfrac<\pi>4\right)>\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin<\left(\alpha\pm \dfrac<\pi>6\right)>\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin<\left(x\pm \dfrac<\pi>3\right)>\\\\ \hline \text<Общий случай>\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt\cdot \sin<(\alpha\pm \phi)>, \ \ \cos\phi=\dfrac a<\sqrt>, \ \sin\phi=\dfrac b<\sqrt>\\\\ \hline \end\]

Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.

Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.

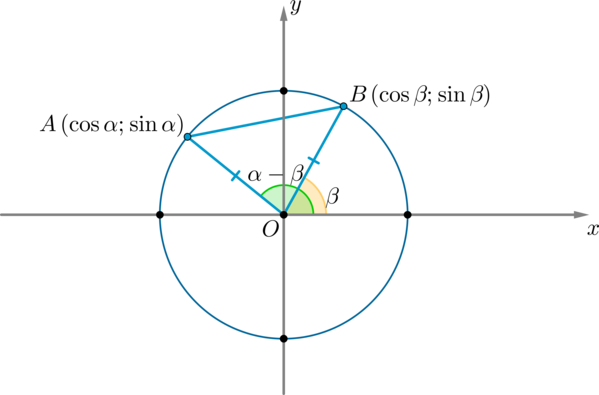
\(\blacktriangleright\) Вывод формулы косинуса разности углов \(\cos<(\alpha -\beta)>=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)

Рассмотрим тригонометрическую окружность и на ней углы \(\alpha\) и \(\beta\) . Пусть этим углам соответствуют точки \(A\) и \(B\) соответственно. Тогда координаты этих точек: \(A(\cos\alpha;\sin\alpha), \ B(\cos\beta;\sin\beta)\) .

Рассмотрим \(\triangle AOB: \ \angle AOB=\alpha-\beta\) . По теореме косинусов:

\(AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)\) (т.к. \(AO=BO=R\) – радиус окружности)

По формуле расстояния между двумя точками на плоскости:

Таким образом, сравнивая равенства \((1)\) и \((2)\) :

Отсюда и получается наша формула.

\(\blacktriangleright\) Вывод остальных формул суммы/разности углов:

Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения \(\sin x=\cos(90^\circ-x)\) и \(\cos x=\sin (90^\circ-x)\) :

разделим числитель и знаменатель дроби на \(\cos\alpha\cos\beta\ne 0\)
(при \(\cos\alpha=0 \Rightarrow \mathrm\,(\alpha\pm\beta)=\mp \mathrm\,\beta\) , при \(\cos\beta=0 \Rightarrow \mathrm\,(\alpha\pm\beta)=\pm \mathrm\,\alpha\) ):

Таким образом, данная формула верна только при \(\cos\alpha\cos\beta\ne 0\) .

5) Аналогично, только делением на \(\sin\alpha\sin\beta\ne 0\) , выводится формула котангенса суммы/разности двух углов.

\(\blacktriangleright\) Вывод формул двойного и тройного углов:

Данные формулы выводятся с помощью предыдущих формул:

1) \(\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha\)

Используя основное тригонометрическое тождество \(\sin^2\alpha+\cos^2\alpha=1\) , получим еще две формулы для косинуса двойного угла:

разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0 \Rightarrow \mathrm\,2\alpha=0\) ):

Таким образом, эта формула верна только при \(\cos\alpha\ne 0\) , а также при \(\cos2\alpha\ne 0\) (чтобы существовал сам \(\mathrm\,2\alpha\) ).

По тем же причинам при \(\sin\alpha\ne 0, \sin2\alpha\ne 0\) .

5) \(\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=\)

6) Аналогично выводится, что \(\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha\)

\(\blacktriangleright\) Вывод формул понижения степени:

Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:

1) \(\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac<1+\cos2\alpha>2\)

2) \(\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac<1-\cos2\alpha>2\)

Заметим, что в данных формулах степень синуса/косинуса равна \(2\) в левой части, а в правой части степень косинуса равна \(1\) .

\(\blacktriangleright\) Вывод формул произведения функций:

1) Сложим формулы косинуса суммы и косинуса разности двух углов:

Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)

2) Если вычесть из формулы косинуса суммы косинус разности, то получим:

3) Сложим формулы синуса суммы и синуса разности двух углов:

\(\blacktriangleright\) Вывод формул суммы/разности функций:

Обозначим \(\alpha+\beta=x, \alpha-\beta=y\) . Тогда: \(\alpha=\dfrac2, \ \beta=\dfrac2\) . Подставим эти значения в предыдущие три формулы:

Получили формулу суммы косинусов.

Получили формулу разности косинусов.

Получили формулу суммы синусов.

4) Формулу разности синусов можно вывести из формулы суммы синусов:

Аналогично выводится формула суммы котангенсов.

\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:

(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\) ):)

2) Так же, только делением на \(\sin^2\alpha\) , выводится формула для косинуса.

\(\blacktriangleright\) Вывод формул вспомогательного угла:

Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.

Рассмотрим выражение \(a\sin x+b\cos x\) . Домножим и разделим это выражение на \(\sqrt\,\) :

\(a\sin x+b\cos x=\sqrt\left(\dfrac a<\sqrt>\sin x+ \dfrac b<\sqrt>\cos x \right)=\sqrt\big(a_1\sin x+b_1\cos x\big)\)

Заметим, что таким образом мы добились того, что \(a_1^2+b_1^2=1\) , т.к. \(\left(\dfrac a<\sqrt>\right)^2+\left(\dfrac b<\sqrt>\right)^2=\dfrac=1\)

Таким образом, можно утверждать, что существует такой угол \(\phi\) , для которого, например, \(\cos \phi=a_1, \ \sin \phi=b_1\) . Тогда наше выражение примет вид:

\(\sqrt\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)

Значит, формула выглядит следующим образом: \[<\large\,\sin (x+\phi),>> \quad \text <где >\cos \phi=\dfrac a<\sqrt>\] Заметим, что мы могли бы, например, принять за \(\cos \phi=b_1, \ \sin \phi=a_1\) и тогда формула выглядела бы как \[a\sin x+b\cos x=\sqrt\,\cos (x-\phi)\]

\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:

\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1<\sqrt2>\sin x\pm\dfrac1<\sqrt2>\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac<\pi>4\right)\)

\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac<\sqrt3>2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac<\pi>6\right)\)

\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac<\sqrt3>2\cos x\right)=2\,\sin\left(x\pm\dfrac<\pi>3\right)\)

Источник