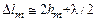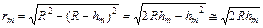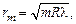Кольца Ньютона
В отраженном свете интерференционная картина является результатом сложения когерентных волн 1 и 2, отраженных от сферической поверхности линзы и от поверхности стеклянной пластинки (рис.9). Интенсивности волн примерно одинаковы, поэтому наблюдается довольно четкая (контрастная) система светлых и темных колец.
Выведем формулу для диаметров темных колец Ньютона в отраженном свете. Темные кольца радиуса rm образуются в тех местах, где разность хода Dlm волн 2 и 1 равна нечетному числу полуволн:
-для радиусов темных интерференционных колец Ньютона
— для радиусов светлых интерференционных колец Ньютона. Рис.9
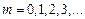
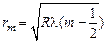
Каждой координате xm, т.е. каждой темной интерференционной полосе (темному кольцу), соответствует определенная толщина воздушной прослойки
(клина) 
под ней
. Поэтому интерференционные полосы в этом случае называют полосами равной (постоянной )толщины.
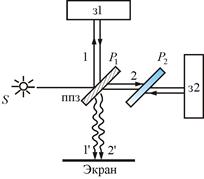
Для наблюдения как полос равного наклона, так и полос равной толщины можно использовать интерферометр Майкельсона (рис. 10). Рассмотрим схему интерферометра Майкельсона: з1 и з2 зеркала. Полупрозрачное зеркало P1 посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 Рис.10
и проходя P1 , дает 1′ , а луч 2, отражаясь от з2 и далее от P1 , дает 2′ . Пластинки P1 и P2 одинаковы по размерам. P2 ставится для компенсации разности хода второго луча. Лучи 1′ и 2′ когерентны и интерферируют.
Лекционные демонстрации
1. Показ фрагмента видеофильма (Длительность всего фильма: 19 мин) Интерференция. Сложение волн. Когерентность Автор сценария: А.Смирнов Консультанты: д.физ-мат.н., профессор Т.Д. Шермергор, к.физ-мат.н. Ю.Иванов, к.физ.-мат.н. С. Пеньков
2. Показ компьютерных демонстраций
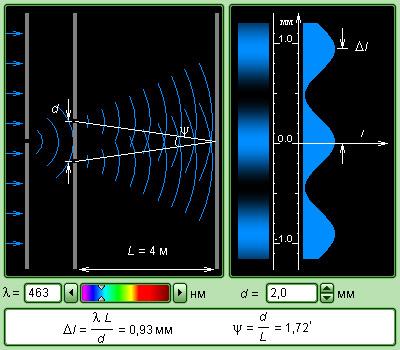
Модель 1. Опыт Юнга.
Компьютерная модель является аналогом интерференционного опыта Юнга. Можно изменять длину световой волны λ и расстояние между щелями d. На дисплее возникает в увеличенном масштабе интерференционная картина и распределение интенсивности на экране. Рис.11
В нижнем окне высвечиваются значения угла ψ сходимости лучей на экране и ширина интерференционных полос.
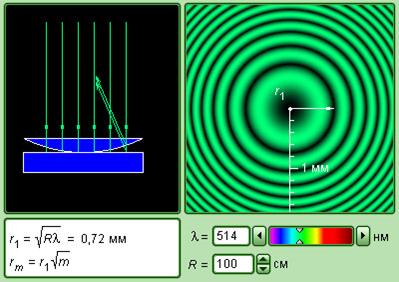
Модель 2. Кольца Ньютона.
Компьютерный эксперимент является аналогом интерференционного опыта Ньютона. Можно изменять длину волны λ света и радиус кривизны R поверхности линзы. На экране возникает в увеличенном масштабе картина колец Ньютона и высвечивается значение радиуса r1 первого темного кольца.
1. Савельев И. В. Курс общей физики, кн. 3. – М.: ООО «Издательство Астрель», ООО «Издательство АСТ», 2004, §§ 4.1-4.5
2. Иродов И. Е. Волновые процессы. Основные законы: Учебное пособие для вузов. – М.: Бином. Лаборатория базовых знаний, 2007, §§4.1 — 4.6.
3. Сивухин Д.В. Общий курс физики. т. 4. М.: ФИЗМАТЛИТ, 2009, §§26-28, 37.
4. Ландсберг Г.С. Оптика. -М. ФИЗМАТЛИТ, 2003, §11.
5. Лосев В.В. Оптические явления. Теория и эксперимент. Учебное пособие, М., 2002, §§2.1 — 2.6.
6. [Электронный ресурс].-М.: Коллекция электронных ресурсов МИЭТ, 2007.- Режим доступа: http://orioks.miet.ru/oroks-miet/srs.shtml
7. Программа обучения. «Открытая Физика 2.6. Часть 2»:
8. Scientific Center «PHYSICON»: of the course «Wave Optics on the Computer»
Источник
Вывести формулу для радиусов темных колец
Волна, отраженная от верхней поверхности линзы, в силу небольшой длины когерентности обычных источников света, некогерентна с волнами, отраженными от поверхностей зазора, и участия в образовании интерференционной картины не принимает. Поэтому мы ее и не будем учитывать.
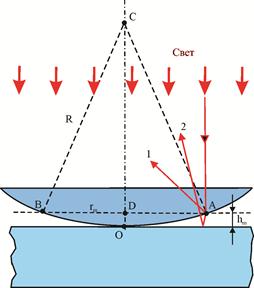
При нормальном падении света кольца в отраженном свете имеют вид концентрических окружностей с центром в точке соприкосновения линзы с пластинкой. Найдем радиусы темных колец (минимумов).
Сначала запишем условие образования темных колец. Они возникают там, где оптическая разность хода волн, отраженных от обеих поверхностей зазора, равна нечетному числу полуволн:
где связано с «потерей» полуволны при отражении от пластинки и . Отсюда
Далее, согласно теореме Пифагора (см. рис. 13), . Учитывая, что , получим
Из (37) и (38) следует, что радиус -го темного кольца
Заметим, что значению соответствует минимум темного пятна (не кольца). Аналогичный расчет можно провести и для светлых колец. Пример . Найдем радиус 5-го светлого кольца, если радиус кривизны выпуклой поверхности линзы и контакт ее с плоской поверхностью стекла идеальный (в точке). Длина волны света . Условие максимумов в данном случае имеет вид
где — толщина зазора в месте — го максимума (заметим, что если бы мы взяли , то значения надо было начинать с нуля). Согласно (38), . Из этих двух соотношений следует, что искомый радиус
Следует обратить внимание на то, что формула (39) справедлива лишь в случае идеального (точечного) контакта сферической поверхности линзы с пластинкой. Но идеальных контактов не бывает, номера колец не равны, вообщя говоря, порядку интерференции , и это обстоятельство необходимо учитывать при расчетах (см. задачу 5 из раздела 1.4 «Примеры решения задач»). Если линзу постепенно отодвигать от поверхности пластинки, то интерференционные кольца будут стягиваться к центру: это ведь кольца (полосы) равной толщины, а она при этом перемещается к центру. С помощью колец Ньютона можно с достаточно высокой точностью контролировать качество изготовления, например, сферических поверхностей. Рассмотрим теперь на конкретном примере вопрос, связанный с причиной локализации колец Ньютона в очень малой области для обычных линз (кольца приходится рассматривать в микроскоп).
Пример . Плосковыпуклая линза, радиус кривизны сферической поверхности которой мм, соприкасается со стеклянной пластинкой. Оценим радиус наблюдаемой в отраженном свете интерференционной картины, если длина волны света и . Свет падает практически нормально. При нормальном падении света ограничивать интерференционную картину будет только длина когерентности . Кольца исчезают при условии , где — ширина зазора в месте исчезновения колец. Согласно (38), , а . Из этих формул получим , откуда
Число видимых колец равно . Этот результат можно получить и с помощью (39).
Источник
Кольца Ньютона
Простая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной и положенной на нее плоско-выпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны. Эта интерференционная картина имеет вид концентрических колец, получивших название кольца Ньютона.
Кольца Ньютона
Возьмите плоско-выпуклую линзу с малой кривизной сферической поверхности и положите ее на стеклянную пластину, как было указано выше. Внимательно разглядывая плоскую поверхность линзы (лучше через лупу), вы обнаружите в месте соприкосновения линзы и пластины темное пятно и вокруг него совокупность маленьких радужных колец. Расстояния между соседними кольцами быстро убывают с увеличением их радиуса. Это и есть кольца Ньютона. Ньютон наблюдал и исследовал их не только в белом свете, но и при освещении линзы одноцветным (монохроматическим) пучком. Оказалось, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному; красные кольца имеют максимальный радиус. Все это вы можете проверить с помощью самостоятельных наблюдений.
Но объяснить, почему возникают кольца Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда волна определенной длины падает почти перпендикулярно на плоско-выпуклую линзу. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны: они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга. Вызываемые ими колебания происходят в одной фазе.
Напротив, если вторая волна отстанет от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.
Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Ведь линии постоянной толщины воздушной прослойки представляют собой окружности. Измерив, радиусы колец, можно вычислить длины волн.
Кольца Ньютона в отражённом свете
Длина световой волны
Длина световой волны. Для красного света измерения дают λ = 8∙10 -7 м, а для фиолетового — λ = 4∙10 -7 м. Длины волн, соответствующие другим цветам спектра, принимают промежуточные значения. Для любого цвета длина световой волны очень мала. Представьте себе среднюю морскую волну длиной в несколько метров, которая увеличилась настолько, что заняла весь Атлантический океан от берегов Америки до Европы. Длина световой волны в том же увеличении лишь ненамного превысила бы ширину этой страницы.
Явление интерференции не только доказывает наличие у света волновых свойств, но и позволяет измерить длину волны. Подобно тому, как высота звука определяется его частотой, цвет света определяется частотой колебаний или длиной волны.
Вне нас в природе нет никаких красок, есть лишь волны разной длины. Глаз — сложный физический прибор, способный обнаруживать различие в цвете, которому соответствует весьма незначительная (около 10 -6 см) разница в длине световых волн. Интересно, что большинство животных не способны различать цвета. Они всегда видят черно-белую картину.
При переходе света из одной среды в другую длина волны изменяется. Это можно обнаружить так. Заполним водой или другой прозрачной жидкостью с показателем преломления п воздушную прослойку между линзой и пластиной. Радиусы интерференционных колец уменьшатся.
Почему это происходит? Мы знаем, что при переходе света из вакуума в какую-нибудь среду скорость света уменьшается в п раз. Так как v=λv, то при этом должна уменьшиться в п раз либо частота, либо длина волны. Но радиусы колец зависят от длины волны. Следовательно, когда свет входит в среду, изменяется в п раз именно длина волны, а не частота.
Источник
Кольца Ньютона
В отраженном свете интерференционная картина является результатом сложения когерентных волн 1 и 2, отраженных от сферической поверхности линзы и от поверхности стеклянной пластинки (рис.9). Интенсивности волн примерно одинаковы, поэтому наблюдается довольно четкая (контрастная) система светлых и темных колец.
Выведем формулу для диаметров темных колец Ньютона в отраженном свете. Темные кольца радиуса rm образуются в тех местах, где разность хода Dlm волн 2 и 1 равна нечетному числу полуволн:
-для радиусов темных интерференционных колец Ньютона
— для радиусов светлых интерференционных колец Ньютона. Рис.9
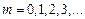
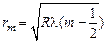
Каждой координате xm, т.е. каждой темной интерференционной полосе (темному кольцу), соответствует определенная толщина воздушной прослойки
(клина) 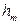под ней. Поэтому интерференционные полосы в этом случае называют полосами равной (постоянной )толщины.
Для наблюдения как полос равного наклона, так и полос равной толщины можно использовать интерферометр Майкельсона (рис. 10). Рассмотрим схему интерферометра Майкельсона: з1 и з2 зеркала. Полупрозрачное зеркало P1 посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 Рис.10
и проходя P1 , дает 1′ , а луч 2, отражаясь от з2 и далее от P1 , дает 2′ . Пластинки P1 и P2 одинаковы по размерам. P2 ставится для компенсации разности хода второго луча. Лучи 1′ и 2′ когерентны и интерферируют.
Лекционные демонстрации
1. Показ фрагмента видеофильма (Длительность всего фильма: 19 мин) Интерференция. Сложение волн. Когерентность Автор сценария: А.Смирнов Консультанты: д.физ-мат.н., профессор Т.Д. Шермергор, к.физ-мат.н. Ю.Иванов, к.физ.-мат.н. С. Пеньков
2. Показ компьютерных демонстраций
Модель 1. Опыт Юнга.
Компьютерная модель является аналогом интерференционного опыта Юнга. Можно изменять длину световой волны λ и расстояние между щелями d. На дисплее возникает в увеличенном масштабе интерференционная картина и распределение интенсивности на экране. Рис.11
В нижнем окне высвечиваются значения угла ψ сходимости лучей на экране и ширина интерференционных полос.
Модель 2. Кольца Ньютона.
Компьютерный эксперимент является аналогом интерференционного опыта Ньютона. Можно изменять длину волны λ света и радиус кривизны R поверхности линзы. На экране возникает в увеличенном масштабе картина колец Ньютона и высвечивается значение радиуса r1 первого темного кольца.
1. Савельев И. В. Курс общей физики, кн. 3. – М.: ООО «Издательство Астрель», ООО «Издательство АСТ», 2004, §§ 4.1-4.5
2. Иродов И. Е. Волновые процессы. Основные законы: Учебное пособие для вузов. – М.: Бином. Лаборатория базовых знаний, 2007, §§4.1 — 4.6.
3. Сивухин Д.В. Общий курс физики. т. 4. М.: ФИЗМАТЛИТ, 2009, §§26-28, 37.
4. Ландсберг Г.С. Оптика. -М. ФИЗМАТЛИТ, 2003, §11.
5. Лосев В.В. Оптические явления. Теория и эксперимент. Учебное пособие, М., 2002, §§2.1 — 2.6.
6. [Электронный ресурс].-М.: Коллекция электронных ресурсов МИЭТ, 2007.- Режим доступа: http://orioks.miet.ru/oroks-miet/srs.shtml
7. Программа обучения. «Открытая Физика 2.6. Часть 2»:
8. Scientific Center «PHYSICON»: of the course «Wave Optics on the Computer»
Источник
