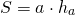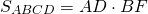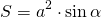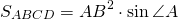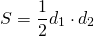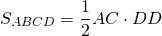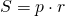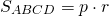- Площадь ромба
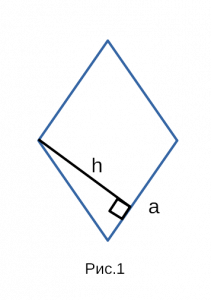
- Площадь ромба по стороне и высоте
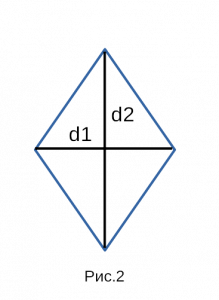
- Площадь ромба по двум диагоналям
- Площадь ромба по углу и противолежащей диагонали
- Площадь ромба по углу и диагонали проведенной из этого угла
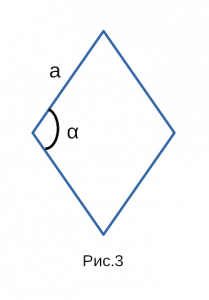
- Площадь ромба по стороне и углу между сторонами
- Площадь ромба по радиусу вписанной окружности и углу между сторонами
- Площадь ромба по радиусу вписанной окружности и стороне
- Таблица с формулами площади ромба
- Определения
- Площадь ромба
- выведите формулу площади ромба с пояснением
- Площади фигур. Площадь ромба.
- Как найти площадь ромба
Площадь ромба
Площадь ромба, формулы и калькулятор для вычисления площади в режиме онлайн.
Для вычисления площади ромба применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади ромба в режиме онлайн.
Площадь ромба по стороне и высоте
Площадь ромба по двум диагоналям
Площадь ромба по углу и противолежащей диагонали
Площадь ромба по углу и диагонали проведенной из этого угла
Площадь ромба по стороне и углу между сторонами
Площадь ромба по радиусу вписанной окружности и углу между сторонами
Площадь ромба по радиусу вписанной окружности и стороне
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади ромба
В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула |
| 1 | сторона и высота |  |
| 2 | диагонали | 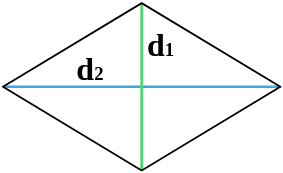 |
| 3 | диагональ и угол между сторонами |  |
| 4 | диагональ и угол между сторонами | 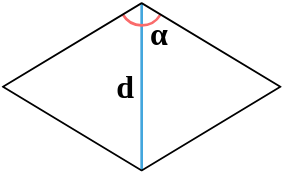 |
| 5 | сторона и угол между сторонами |  |
| 6 | радиус вписанной окружности и угол между сторонами | 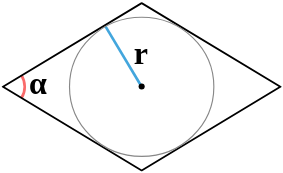 |
| 7 | сторона и радиус вписанной окружности | 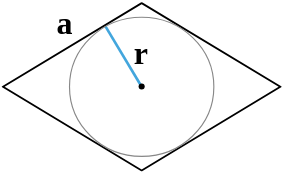 |
Определения
Ромб — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.
Ромб – это частный случай параллелограмма.
Высота ромба – это отрезок проведенный из вершины ромба к противоположной стороне под углом в 90 градусов.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Площадь ромба – это численная характеристика, характеризующая размер плоскости, ограниченной четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.
Источник
Площадь ромба
Площадь ромба можно найти по формулам для нахождения площади параллелограмма. С учётом свойств ромба, некоторые из этих формул меняют свой вид.
I. Площадь ромба по стороне и высоте
Площадь ромба равна произведению стороны ромба и его высоты.
Формула для нахождения площади ромба по стороне и высоте не отличается от соответствующей формулы площади параллелограмма:

Так как все стороны ромба равны и все его высоты равны, для нахождения площади можно брать любую сторону и любую высоту.
II. Площадь ромба по стороне и углу
Площадь ромба равна произведению квадрата его стороны на синус угла.
Формула для нахождения площади ромба через сторону и угол:

Так как ∠D=180-∠A, sin∠D=sin(180-∠A)=sin∠A, то для нахождения площади можно брать синус любого угла.
III. Площадь ромба через его диагонали
Площадь ромба равна половине произведения его диагоналей.
Формула для нахождения площади ромба по его диагоналям
по сравнению с соответствующей формулой площади параллелограмма упрощается (так как диагонали ромба взаимно перпендикулярны, а синус прямого угла равен единице).

IV. Площадь ромба через радиус вписанной окружности
Площадь ромба равна произведению его полупериметра на радиус вписанной окружности.
Формула для нахождения площади ромба через радиус вписанной окружности
аналогов среди формул для нахождения площади параллелограмма не имеет (поскольку из всех параллелограммов окружность можно вписать только в ромб и квадрат).

Так как полупериметр ромба равен p=2a, формулу можно записать в виде
Источник
выведите формулу площади ромба с пояснением
О, да здесь она не одна будет. Но вот две основные:
1) Площадь ромба равна половине произведения его диагоналей.
Так как ромб состоит из четырех прямоугольных треугольников, то его площадь равна сумме площадей этих треугольников.
Площадь прямоугольного треугольника равна половине произведения его катетов.
Допустим, у нас ромб ABCD. Диагонали его (AC и BD) пересекаются в точке О.
Тогда: S = 0,5*AO*BO + 0,5*BO*OC + 0,5*OC*OD + 0,5*OD*OA
Вынесем 0,5 за скобку и сделаем ещё группировку внутри скобок:
S = 0,5*(OB*(OA+OC) + OD*(OA+OC))
OA+OC=AC
Значит: S = 0,5*(AC*(OB+OD))
OB+OD=BD
то есть, S = 0,5*AC*BD
Что и требовалось доказать.
2) Площадь ромба равна полу периметру, умноженному на радиус вписанной окружности.
S=pr
Опять возьмем ромб ABCD. Так как все стороны равны, то заменим из просто на переменную a. Впишем в этот ромб окружность с радиусом r.
И, конечно, проведем диагонали. Вновь видим, что площадь ромба состоит из суммы площадей четырех прямоугольных треугольников.
В одном каком-нибудь треугольнике опустим из точки пересечения диагоналей (то бишь вершины прямого угла) на гипотенузу (она же сторона ромба) перпендикуляр. Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне. Значит, площадь одного такого треугольника равна S = 0,5*a*r
А таких треугольников 4.
Площадь ромба S = 4*a*r / 2
4*a = P, то есть, периметр.
P/2 = p, то есть, полу периметр.
Замещаем и получаем: S = pr
Источник
Площади фигур. Площадь ромба.
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, полностью принадлежащей
одной плоскости. Если фигуру можно разбить на конечное множество единичных квадратов, то площадь
будет равна числу этих квадратов.
Ромб — это параллелограмм с равными сторонами. Ромб с прямыми углами называется квадратом.
Площадь ромба равна половине произведения его диагоналей.
Воспользуйтесь нашим калькулятором для расчета площади ромба.
Для расчета площади других фигур воспользуйтесь этим калькулятором: площади фигур.
Формулы для вычисления площади ромба.
- Формула площади ромба по длине стороны и его высоте.
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
- Формула площади ромба по длине стороны и углу.
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
- Формула площади ромба по длинам его диагоналей.
Площадь ромба равна половине произведению длин его диагоналей.
где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.

Еще некоторые формулы для определения площади ромба:
Источник
Как найти площадь ромба
Площадь ромба можно вычислить разными способами.
Например, через половину произведения двух диагоналей
друг на друга, через синус и сторону в квадрате…
Также, площадь ромба равна площади параллелограмма.
Как следствие, так, как ромб является параллелограммом, с
равными сторонами, поэтому площадь ромба
можно найти через площадь параллелограмма.
Для ромба истинны и верны все свойства параллелограмма.
Формула площади ромба и формула
площади параллелограмма одинаковая.
Ромб — параллелограмм, у которого
все четыре стороны равны.
Формулировка площади ромба через параллелограмм:
Формула площади ромба через параллелограмм:
a — основание; h — высота;
Площадь ромба, можно также найти другим способом. Для
этого мысленно разделим ромба на четыре треугольника,
так чтобы каждая вершина была соединена с противоположной
вершиной. Получившиеся линии называют диагоналями. Если
известны длины двух диагоналей ромба, то можно найти площадь.
Формула площади ромба через две диагонали:
\( S = \frac<1>2d_1 d_2 \)
d1 и d2 — диагонали;
В самых редких случаях, если известен синус и одна из сторон,
используют формулу площади ромба через синус и квадрат стороны.
Формулировка площади ромба через синус и сторону в квадрате:
Формула площади ромба через синус и сторону в квадрате:
a — сторона; sin α — синус угла;
Рис. 1 — площадь ромба через площадь параллелограмма / основание и высоту.
Рис. 2 — площадь ромба через две диагонали
Рис. 3 — площадь ромба через синус и сторону в квадрате
Также, вы можете прочитать про свойства и признаки ромба.
Источник