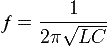Вывести формулу для определения резонансной частоты колебаний

Резонанс

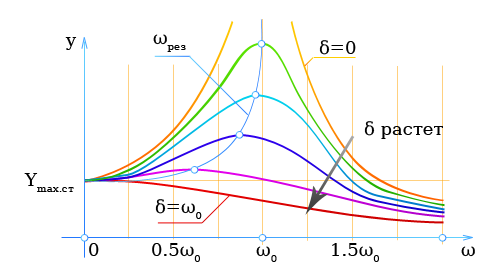
При заданных возмущающей силе F max.возм и коэффициенте трения β амплитуда Y m является функцией только угловой частоты возмущающей силы.

На рисунке показана зависимость Y m от ω (резонансная кривая). Параметром служит коэффициент затухания δ.

При ω ≈ ω₀ она достигает особенно большого значения (резонанс).

При самых малых значениях δ величина Y m резко возрастает.

Если δ > 0 , то в случае резонанса ω ω₀; величина Y max.ст представляет собой статическое отклонение системы под действием постоянной силы Y max.возм ( ω = 0 ).

Для определения резонансной частоты необходимо найти максимум функции Ym = Ym(ω) и приравнять первую производную нулю; тогда, если

ωрез	резонансная частота, при которой амплитуда максимальна,	радиан/сек
ω0	частота собственных незатухающих колебаний системы,	радиан/сек
m	масса колебательной системы,	кг
β	коэффициентом вязкого трения,	кг/сек
δ	коэффициентом затухания,	радиан/сек

Частота резонанса

Резонансная частота ω_рез несколько меньше частоты ω собственных колебаний системы с затуханием.

Условие отсутствия резонанса

При условии (2) явление резонанса совершенно исчезает. В этом случае при любой частоте возмущающей силы амплитуда колебаний меньше статического отклонения.

Амплитуда резонанса

Чтобы найти величину амплитуды в резонансном случае, нужно подставить формулу (1) в формулу отклонения при вынужденных колебаниях.

Ymax.рез	резонансная амплитуда колебаний системы,	метр
Fmax.возм	максимальное значение возмущающей силы,	Ньютон
m	масса колебательной системы,	кг
ωрез	резонансная частота, при которой амплитуда максимальна,	радиан/сек
ω0	частота собственных незатухающих колебаний системы,	радиан/сек
ω	частота колебаний системы с затуханием,	радиан/сек
β	коэффициентом вязкого трения,	кг/сек
δ	коэффициентом затухания,	радиан/сек

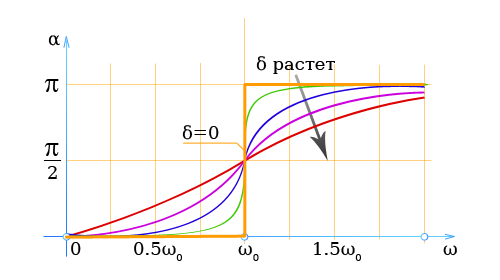
Согласно формуле, разность фаз α также зависит от частоты возмущающей силы. Параметром служит коэффициент δ.

Независимо от величины затухания при ω = ω₀ разность фаз составляет

Резонанс играет большую роль в технике и в повседневной жизни. В большинстве механических устройств под действием внешних периодических сил могут возникать колебания. При резонансе происходит нарастание амплитуды колебаний, и это может привести к разрушениям («резонансная катастрофа»). В случае вращательного движения резонансную частоту называют критическим числом оборотов.

Чтобы предотвратить возникновение колебаний со слишком большой амплитудой следует:
— по возможности устранять периодически действующие силы,
— добиваться большой разности собственной частоты и частоты возбуждающей силы,
— добиваться того, чтобы частота принимала резонансное значение лишь на время, меньшее одного периода колебаний,
— применять демпфирующие элементы.

Источник

Резонансная частота: формула

Галилео Галилей, исследуя маятники и музыкальные струны, описал явление, которое впоследствии стали называть резонансом. Оно проявляется не только в акустике, но и в механике, электронике, оптике и астрофизике. Резонансный эффект имеет как положительные, так и отрицательные воздействия на колебательные системы.

Эффект резонанса

Ярким примером механического класса резонаторов является пружинный маятник. Профессор из технологического Массачусетского института (в Америке), В. Левин, акцентирует внимание своих студентов на то, что резонанс (resonance) – это эффект, сопряжённый с увеличением амплитуды. Для демонстрации явления используется установка. Она состоит из следующих компонентов:

• электродвигатель;
• механизм, превращающий вращение в возвратно-поступательное движение;
• ЛАТР – лабораторный автотрансформатор;
• медная пружина из проволоки с набором грузиков;
• направляющая для пружины.

Направление колебания пружины – вертикальное. Вращение вала мотора заставляет пружину совершать колебания. С помощью автотрансформатора присутствует возможность регулировать напряжение. Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.

Перед опытом замеряется удлинение медной пружины под действием грузиков (для оценки резонансной частоты пружины). Изменение скорости вращения вала заставляет амплитуду колебания конца пружины с грузом изменяться. Амплитуда увеличивается и на 1-м герце частоты становится максимальной (

Важно! При дальнейшем увеличении скорости вращения вала амплитуда конца пружины начинает уменьшаться. Это означает, что resonance пройден. Если уменьшать напряжение, а с ним и частоту вращения двигателя, снова можно наблюдать эффект resonance колебания пружины.

Добротность пружины Q определяется как отношение амплитуды колебания пружины Aпр к амплитуде колебания вынуждающей силы Aвс. В этом случае Q = Aпр/Aвс = 30/5 = 6, где Aвс = 5.

Определение колебательного контура

Резонансные явления, отмеченные в электротехнике, ярко выражены в схемах колебательных контуров (КК). Подобные конструкции представляют собой элементарные системы, способные осуществлять свободные колебания электромагнитной природы. Сам КК в цепи состоит из следующих элементов:

• конденсатора;
• катушки индуктивности;
• источника тока.

Внимание! Выводы элементов схемы могут соединяться друг с другом параллельно или последовательно. Все зависит от того, какого результата нужно добиться от резонанса в КК.

Подключение к цепи индуктивной катушки

Включение в ёмкостную цепь катушки индуктивности сразу превращает её в КК. В зависимости от схемы подключения, различают два вида КК 1 класса: параллельный и последовательный.

Параллельный КК

В данной схеме конденсатор С соединён с катушкой L параллельно. Если заряженный конденсатор присоединить к катушке, то энергия, запасённая в нём, передастся ей. Через индуктивную катушку L потечёт ток, вызывая электродвижущую силу (ЭДС).

ЭДС самоиндукции L будет направлена на снижение тока в параллельной цепи. Ток, созданный этой ЭДС, и ток разряда ёмкости сначала одинаковы, а их суммарное значение равно нулю. Конденсатор передаст свою энергию Ec в катушку и полностью разрядится. Индуктивность, получив максимальную магнитную энергию EL, начнёт заряжать ёмкость напряжением уже другой полярности. Когда вся энергия из индуктивности перейдёт в ёмкость, конденсатор будет полностью заряжен. В цепи появляются колебания, такой контур называется колебательным.

К сведению. Если бы в такой цепи отсутствовали потери, то такие колебания никогда не стали затухать. На практике, продолжительность процесса зависит от потери энергии. Чем больше потери, тем меньше длительность колебаний.

Параллельное соединение C и L вызывает резонанс токов. Это значит, что токи, проходящие через C и L, выше по значению, чем ток через сам контур, в конкретное число раз. Это число носит название добротности Q. Оба тока (емкостной и индуктивный) остаются внутри цепи, потому что они находятся в противофазе, и происходит их обоюдная компенсация.

Стоит отметить! На fрез величина R КК устремляется к бесконечности.

Последовательный КК

В этой схеме соединены последовательно друг с другом катушка и конденсатор.

В такой схеме происходит resonance напряжений, R контура устремляется к нулю в случае образования резонансной частоты (fрез). Это позволяет использовать подобную систему резонанса в качестве фильтра.

Резонансная частота

При подаче на два КК (параллельного и последовательного) переменного напряжения с изменяющейся частотой их реактивные сопротивления C и L будут меняться. Изменения происходят следующим образом:

• с увеличением f – ёмкостное сопротивление уменьшается, а индуктивное увеличивается;
• с уменьшением f – ёмкостное сопротивление увеличивается, а индуктивное уменьшается.

Частота, при которой реактивные сопротивления обоих элементов контура равны, называется резонансной.

Важно! При fрез сопротивление параллельного КК будет максимальным, а последовательного КК – минимальным.

Резонансная частота формула, которой имеет вид:

где:

• L – индуктивность, Гн;
• C – ёмкость, Ф.

Подставляя известные значения ёмкости и индуктивности в формулу резонансной частоты колебательного контура любой конфигурации, можно рассчитать этот параметр.

Для определения периода колебаний КК и частоты резонанса можно воспользоваться онлайн калькулятором на соответствующем портале в сети. Профессиональная программа имеет несложный интерфейс.

Применение колебательных контуров

Подробный расчет колебательного контура позволяет точно подбирать величину необходимых элементов КК. Это позволяет использовать их в схемах электроники в виде:

• частотных фильтров – в радиоприёмниках, генераторах сигналов, преобразователях и выпрямителях;
• колебательных контуров – для выделения и настройки на определённую частоту станции вещания;
• силовых resonance-фильтров – для формирования напряжения синусоидальной формы.

На самолётах гражданской авиации КК применяется в блоках регулировки частоты генераторов.

Условие отсутствия резонанса

Для того чтобы возник резонанс формула которого для тока равна ω0*C = 1/ ω0*L, необходимо выполнения этого равенства. Существуют условия для невозможности появления этого эффекта, а именно:

• отсутствие у системы собственных колебаний;
• невозможность совпадения частоты внешнего воздействия с собственной частотой системы.

Амплитуда резонанса

В КК при подаче переменного напряжения от внешнего источника наблюдаются два вида резонанса и резкое увеличение двух видов амплитуды: амплитуды тока и амплитуды напряжения.

Амплитуда тока

Амплитуда тока резко возрастает при резонансе напряжений в последовательном контуре (последовательный резонанс). Источник переменной ЭДС включён в цепь, где нагрузкой служат последовательно включённые элементы L и С.

В этом случае в цепь входят сопротивления: активное r и реактивное x, равное:

Так как для внутренних колебаний xL и xC равны, то для тока, поступающего от генератора, при резонансе (когда частоты совпадают) эти значения тоже одинаковы. Поэтому x = 0. В итоге полное сопротивление цепи будет состоять только из небольшого активного сопротивления. Ток при этом получается максимальным.

Амплитуда напряжения

Резонанс токов (параллельный резонанс) является условием резкого возрастания амплитуды напряжения. Источник ЭДС подключается вне контура и нагружен параллельно соединёнными элементами L и С. В этом случае на эффект резонанса влияет внутреннее сопротивление генератора. Амплитуда напряжения на контуре максимальна при малом отличии напряжения контура от напряжения генератора. Это возможно при малом Ri.

Внимание! Изменение частоты генератора меняет ток, а амплитуда напряжения на контуре не отстаёт по величине от напряжения на генераторе. Если, U = Е — I*Ri, где Е – ЭДС, I – ток, то при малом Ri U = Е.

Формула для определения расчётной резонансной частоты для разных колебательных систем различается по входящим в неё параметрам. Несмотря на все различия, суть остаётся неизменной: эффект резонанса наступает тогда, когда частота внутренних колебаний системы и внешних воздействий становятся равны друг другу.

Видео

Источник

Колебательный контур LC

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC.

Основные свойства индуктивности

— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Природа электромагнитных колебаний в контуре

Период свободных колебаний контура LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.

Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t₁, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t₁ = .
По истечении времени t₁, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t₂ = t₁, он перезарядит конденсатор от нулевого до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t₁ и t₂ составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t₃, сменив полярность полюсов.

В течении заключительного этапа колебания (t₄), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t₁ + t₂ + t₃ + t₄ составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T

Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности X_L=2πfL равно реактивному сопротивлению ёмкости X_C=1/(2πfC).

Расчёт частоты резонанса LC-контура:

Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Источник