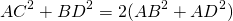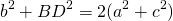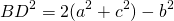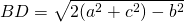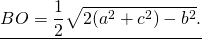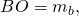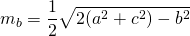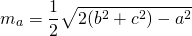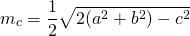Вывести формулу для медиан треугольника

По сторонам треугольника найти его медиану

Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.

Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.

Дано: ∆ ABC,

сторона AC — наибольшая,

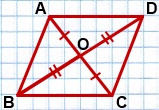
1) На луче BO отложим отрезок OD, OD=BO.

2) Проведем отрезки AD и CD.

3) Рассмотрим четырехугольник ABCD.

AO=CO (так как BO — медиана треугольника ABC по условию);

BO=DO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

так как BO=1/2 BD (по построению),

Если ввести обозначение

формула для нахождения медианы треугольника по его сторонам примет вид:

Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.

Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.

Соответственно, формулы для нахождения длины медианы в этих случаях:

Приём, который применили для решения задачи — метод удвоения медианы.

Источник

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Источник

Теорема косинусов. Следствия из теоремы косинусов. 9-й класс

Класс: 9

Тип урока: Урок – семинар.

Вид урока: Урок формирования умений и навыков, применения теоремы косинусов, ее следствий при решении задач и доказательства теорем.

• Образовательные:
  1. Совершенствовать навыки решения задач с использованием теоремы косинусов и ее следствий.
  2. Вывести формулу о медиане треугольника и показать применение этой формулы при решении задач.
  3. Ознакомить учащихся с методом дополнительных построений при выводе формул и при решении задач.
• Развивающая:
  1. Формирование и совершенствование умений обобщать путем сравнения, постановка и решение проблем, рассуждение по аналогии, оперирование уже знакомыми геометрическими понятиями и фактами.
  2. Развивать психологические характеристики личности учащихся: выдвижению гипотез, формированию проблем.
  3. Развивать психические свойства: память, воображение.
• Воспитательные:
  1. Отрабатывать навыки устной речи.
  2. Воспитывать умение слушать друг друга и учителя.

1. Организационный момент.

• Приветствие.
• Сегодня мы с вами продолжим работу по теме : “Теорема косинусов и ее следствия”. Используя метод дополнительного построения, выведем формулы для вычисления медиан треугольника и применим ее при решении задач.

2. Проверка домашнего задания.

• Устно формулируем теорему косинусов, ее следствия.
• Анализируем ответы и этапы решения домашних задач.

Определите вид треугольника заданного своими сторонами 17, 8,15.

Наибольший угол лежит против стороны, равной 17, то по следствию из теоремы косинусов:

Ответ: треугольник прямоугольный.

Найдите сторону АВ в треугольнике АВС,

Найдите сторону АС равнобедренного треугольника АВС , если АВ=ВС=4 и медиана АД равна 3.

3. Вывод формулы для вычисления медианы треугольника, если известны все стороны треугольника.

Найдите медиану треугольника АВС с известными сторонами а,в,с.

Отложим отрезок ДК на продолжении медианы ВД, равный ВД. Соединим точки А, К и С,К. Получившийся четырехугольник параллелограмм по признаку( диагонали четырехугольника пересекаются и точкой пересечения делятся пополам).

Применим следствие из теоремы косинусов для параллелограмма:

ВК 2 + АС 2 = 2АВ 2 + 2ВС 2

Значит, (2m_в) 2 + в 2 = 2с 2 + 2а 2 или 4m_в 2 = 2с 2 + 2а 2 – в 2

Запишем аналогичные формулы, для медиан проведенные к другим сторонам:

Решим домашнюю задачу с использованием этой формулы.

Делаем вывод о том, какое решение рациональней.

4. Вопрос: Можно ли найти сторону треугольника, если известны все ее медианы? Выведем формулу для вычисления стороны треугольника по ее медианам. Для этого воспользуемся опять дополнительным построением.

Учащийся у доски выводит формулу.

– Какое дополнительное построение будем проводить?

– Какую фигуру получили и почему?

– Какую теорему будем применять?

Применим следствие из теоремы косинусов для параллелограмма АОСО₁:

Аналогично для других сторон :

Зная метод вывода формулы, всегда можно ее получить.
Применим эту формулу для решения задач. Учащиеся самостоятельно решают, затем проверка на доске.

№ 1 В треугольнике АВС сторона АС равна 20, а медианы , проведенные к другим сторонам равны 18 и 24 соответственно. Найдите третью медиану треугольника.

Метод дополнительного построения используется и при решении задач.

№ 2 Найдите площадь остроугольного треугольника АВС,

5. Подведение итогов урока:

• Какие новые формулы изучили на уроке?
• Какой метод применяли для доказательства теорем и решения задач?

6. Домашнее задание:

1. Найдите площадь треугольника, если две стороны его соответственно равны 27 и 29, а медиана проведенная к третьей стороне равна 26.
2. Найдите площадь остроугольного треугольника АВС,

Математика, правильно понятая, обладает не только истинной, но так же величайшей красотой.
Бертран Рёссель

Источник

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

• AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
• AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

Источник