Вывести формулу для эдс холла
Одним из проявлений магнитной составляющей силы Лоренца в веществе служит эффект, обнаруженный в 1879 г. американским физиком Э.Г. Холлом (1855–1938). Эффект состоит в возникновении на боковых гранях проводника с током, помещенного в поперечное магнитное поле, разности потенциалов, пропорциональной величине тока I и индукции магнитного поля В.
Рассмотрим эффект, обусловленный действием лоренцевой силы 

В случае изображенном на рис. 2.19, а, верхняя часть проводника будет заряжаться отрицательно, в случае 2.19, б – положительно.
Это позволяет экспериментально определить знак носителя заряда в проводнике.
При равной концентрации носителей заряда обоих знаков возникает холловская разность потенциалов, если различна подвижность, т.е. дрейфовая скорость носителей заряда.
Подсчитаем величину холловской разности потенциалов (Uх).
Обозначим: Ex – напряженность электрического поля, обусловленного ЭДС Холла, h – толщина ленты проводника.
 , , | (2.10.1) |
Перераспределение зарядов прекратится, когда сила qEx уравновесит лоренцеву силу, т.е.

Плотность тока 


 , , | (2.10.2) |
где 
Исследования ЭДС Холла привели к удивительным выводам. Металлы могут обладать проводимостью р-типа (Zn, Cd – у них дырки более подвижные, чем электроны). Это металлы с чуть перекрывающимися знаками, т.е. полуметаллы.
Из формулы (2.10.2) можно найти число носителей заряда:
 , , | (2.10.3) |
Итак, измерение холловской разности потенциалов позволяет определить:
· знак заряда и тип носителей;
На рисунке 2.20 показана установка для исследования магнитного поля длинного соленоида с помощью датчика Холла.
Источник
Теория метода. ЭДС Холла находится по формуле:



ЭДС Холла находится по формуле:
где R – постоянная Холла, j – плотность тока, текущего через образец, b – толщина образца, а – его ширина, В – индукция магнитного поля, I – сила тока в образце (j=I/S=I/ab).
Для двух разных значений силы тока, текущего через датчик Холла, ЭДС Холла можно найти по формулам:
Вычитая из второго выражения первое, получим:
Если построить график зависимости UH от I, то он будет выражаться прямой линией, и К= Δ UH/Δ I=RB/a будет являться угловым коэффициентом для этой прямой.
Если определить К для разных значений индукции В и построить график зависимости К от В, то этот график также будет выражаться прямой (зависимость прямо пропорциональная). Угловой коэффициент для этого графика:
β= ΔК/ΔВ=R/a.Измерив β, можно найти постоянную Холла по формуле:
R=βa.(1)
Зная постоянную Холла, можно определить концентрацию носителей по формуле:
n=1/Re(2)
где e – элементарный заряд.
Описание установки
Установка состоит из объекта исследования и измерительного устройства.
Объект исследования содержит электромагнит и датчик Холла.
На передней панели измерительного устройства имеются следующие органы управления и индикации:
— кнопки НАПРАВЛЕНИЕ и ТОК «+», «- « задают значение тока через датчик Холла и через электромагнит (для увеличения значения тока нажимается «+», для уменьшения – «-«; нажатием кнопки СБРОС значения тока сбрасываются и одновременно меняется полярность, то есть направление соответствующего тока.
-ЭЛ.МАГНИТ-ДАТЧ.ХОЛЛА включает индикацию тока электромагнита или датчика Холла;
-табло мА и мВ показывают значения тока через датчик Холла или электромагнит (см.индикацию) и ЭДС Холла.
Порядок выполнения работы
1. Включите установку.
2. Выберите полярность источников питания для датчика Холла и электромагнита нажатием соответствующих кнопок.
3. Кнопкой ЭЛ.МАГНИТ-ДАТЧ.ХОЛЛА включите индикацию тока электромагнита и задайте ток электромагнита i=3,2 мА. Переключите эту кнопку на индикацию тока датчика Холла и, увеличивая ток с интервалом 0,5 мА, измерьте значения ЭДС Холла для 8-10 значений силы тока I через датчик Холла. Нажатием кнопки «СБРОС» измените направление тока через датчик (или через электромагнит – по указанию преподавателя) и повторите измерения.
Проведите аналогичные измерения еще для 2-х значений тока через электромагнит (задаются преподавателем в интервале от 3,2 мА до 6 мА ). Результаты измерений занесите в таблицу 1.
Источник
Эффект Холла
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ
Кафедра физики
студент группы 32СУ1
преподаватель Скидан В.В.
Объяснение эффекта Холла с помощью электронной теории
Эффект Холла в ферромагнетиках
Эффект Холла в полупроводниках
Эффект Холла на инерционных электронах в полупроводниках
Датчик ЭДС Холла
Список используемой литературы
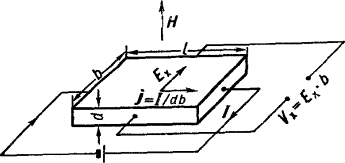
Рис 1.1
Ex = RHj sin a , (1)
где a угол между векторами Н и J ( a ). Когда H ^ j , то величина поля Холла Ех максимальна: Ex = RHj . Величина R , называемая коэффициентом Холла, является основной характеристикой эффекта Холла. Эффект открыт Эдвином Гербертом Холлом в 1879 в тонких пластинках золота. Для наблюдения Холла эффекта вдоль прямоугольных пластин из исследуемых веществ, длина которых l значительно больше ширины b и толщины d , пропускается ток:
здесь магнитное поле перпендикулярно плоскости пластинки. На середине боковых граней, перпендикулярно току, расположены электроды, между которыми измеряется ЭДС Холла Vx :
Так как ЭДС Холла меняет знак на обратный при изменении направления магнитного поля на обратное, то Холла эффект относится к нечётным гальваномагнитным явлениям.
Простейшая теория Холла эффекта объясняет появление ЭДС Холла взаимодействием носителей тока (электронов проводимости и дырок) с магнитным полем. Под действием электрического поля носители заряда приобретают направленное движение (дрейф), средняя скорость которого (дрейфовая скорость) vдр ¹ 0 . Плотность тока в проводнике j = n*evдр , где n — концентрация числа носителей, е — их заряд. При наложении магнитного поля на носители действует Лоренца сила: F = e[Hvдp] , под действием которой частицы отклоняются в направлении, перпендикулярном vдр и Н . В результате в обеих гранях проводника конечных размеров происходит накопление заряда и возникает электростатическое поле — поле Холла. В свою очередь поле Холла действует на заряды и уравновешивает силу Лоренца. В условиях равновесия eEx = еНvдр , Ex =1/ne Hj , отсюда R = 1/ne (cм з /кулон). Знак R совпадает со знаком носителей тока. Для металлов, у которых концентрация носителей (электронов проводимости) близка к плотности атомов ( n » 10 22 См -3 ), R
10 -3 (см 3 /кулон), у полупроводников концентрация носителей значительно меньше и R
10 5 (см 3 /кулон). Коэффициент Холла R может быть выражен через подвижность носителей заряда m = е t /m* и удельную электропроводность s = j/E = еnvлр/Е :
Здесь m* — эффективная масса носителей, t — среднее время между двумя последовательными соударениями с рассеивающими центрами.
Иногда при описании Холла эффекта вводят угол Холла j между током j и направлением суммарного поля Е : tg j = Ex/E= W t , где W — циклотронная частота носителей заряда. В слабых полях ( W t угол Холла j » W t , можно рассматривать как угол, на который отклоняется движущийся заряд за время t . Приведённая теория справедлива для изотропного проводника (в частности, для поликристалла), у которого m* и t их— постоянные величины. Коэффициент Холла (для изотропных полупроводников) выражается через парциальные проводимости s э и s д и концентрации электронов nэ и дырок nд :
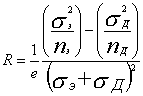
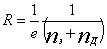
При nэ = nд, = n для всей области магнитных полей :
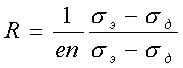
а знак R указывает на преобладающий тип проводимости.
Для металлов величина R зависит от зонной структуры и формы Ферми поверхности. В случае замкнутых поверхностей Ферми и в сильных магнитных полях ( W t »1) коэффициент Холла изотропен, а выражения для R совпадают с формулой 4,б. Для открытых поверхностей Ферми коэффициент R анизотропен. Однако, если направление Н относительно кристаллографических осей выбрано так, что не возникает открытых сечений поверхности Ферми, то выражение для R аналогично 4,б.
2. Объяснение эффекта Холла с помощью электронной теории.
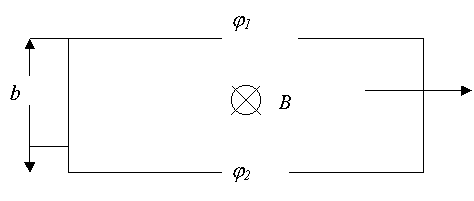
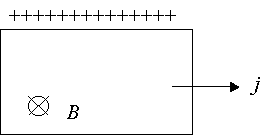
Если металлическую пластинку, вдоль которой течет постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлениям тока и поля возникает разность потенциалов U= j 1— j 2 (смотри рис 2.1). Она называется Холловской разностью потенциалов (в предыдущем пункте – ЭДС Холла) и определяется выражением:
Здесь b — ширина пластинки, j — плотность тока, B — магнитная индукция поля, R — коэффициент пропорциональности, получивший название постоянной Холла. Эффект Холла очень просто объясняется электронной теорией, отсутствие магнитного поля ток в пластинке обусловливается электрическим полем Ео (смотри рис 2.2). Эквипотенциальные поверхности этого поля образуют систему перпендикулярных к вектору Ео скоростей. Две из них изображены на рисунке сплошными прямыми линиями. Потенциал во всех точках каждой поверхности, а следовательно, и в точках 1 и 2 одинаков. Носители тока — электроны — имеют отрицательный заряд, поэтому скорость их упорядоченного движения и направлена противоположно вектору плотности тока j .
При включении магнитного поля каждый носитель оказывается под действием магнитной силы F , направленной вдоль стороны b пластинки и равной по модулю
В результате у электронов появляется составляющая скорости, направленная к верхней (на рисунке) грани пластинки. У этой грани образуется избыток отрицательных, соответственно у нижней грани — избыток положительных зарядов. Следовательно, возникает дополнительное поперечное электрическое поле ЕB . Тогда напряженность этого поля достигает такого значения, что его действие на заряды будет уравновешивать силу (2.2), установится стационарное распределение зарядов в поперечном направлении. Соответствующее значение EB определяется условием: eEB=euB . Отсюда:
Поле ЕB складывается с полем Ео в результирующее поле E . Эквипотенциальные поверхности перпендикулярны к вектору напряженности поля. Следовательно, они повернутся и займут положение, изображенное на рис. 2.2 пунктиром. Точки 1 и 2, которые прежде лежали на одной и той же эквипотенциальной поверхности, теперь имеют разные потенциалы. Чтобы найти напряжение возникающее между этими точками, нужно умножить расстояние между ними b на напряженность ЕB :
Выразим u через j , n и e в соответствии с формулой j=neu . В результате получим:
Последнее выражение совпадает с (2.1), если положить
Из (2.4) следует, что, измерив постоянную Холла, можно найти концентрацию носителей тока в данном металле (т. е. число носителей в единице объема).
Важной характеристикой вещества является подвижность в нем носителей тока. Подвижностью носителей тока называется средняя скорость, приобретаемая носителями при напряженности электрического поля, равной единице. Если в поле напряженности Е носители приобретают скорость u то подвижность их u0 равна:
Подвижность можно связать с проводимостью
Измерив постоянную Холла R и проводимость s , можно по формулам (2.4) и (2.6) найти концентрацию и подвижность носили тока в соответствующем образце.
 | ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||







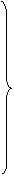




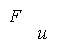
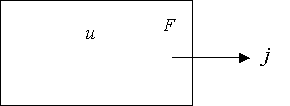



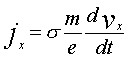 , (1)
, (1)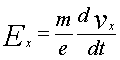 , (2)
, (2)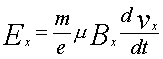 (3)
(3)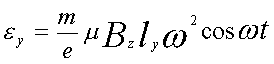 (6)
(6)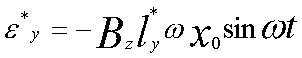 (7)
(7)






