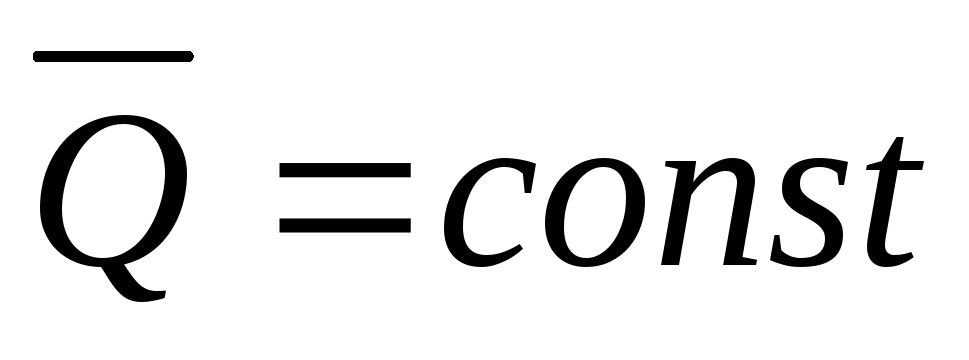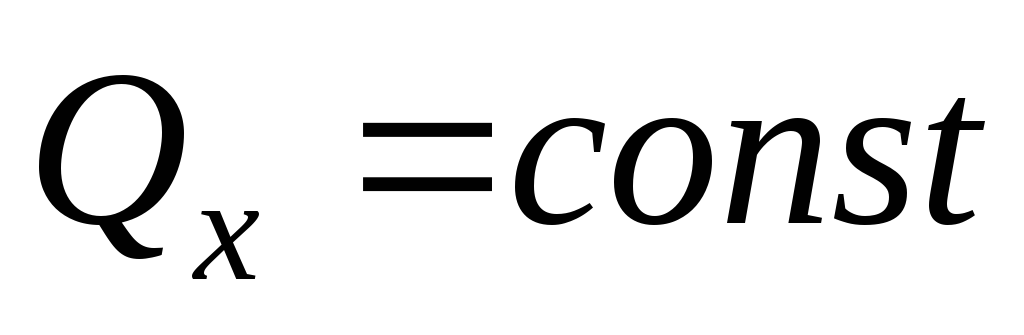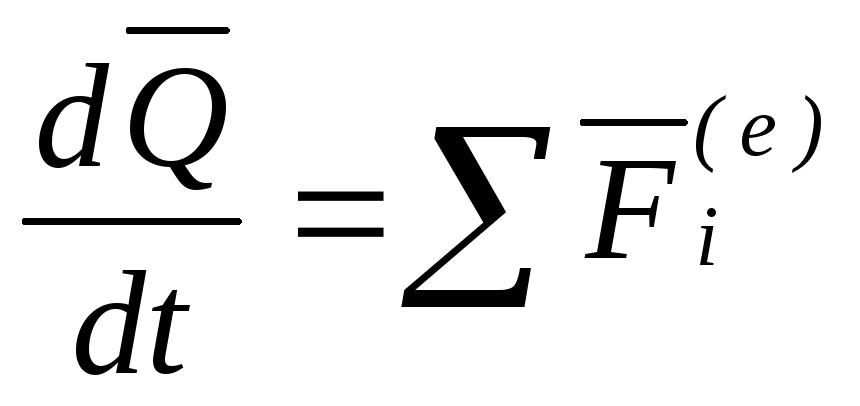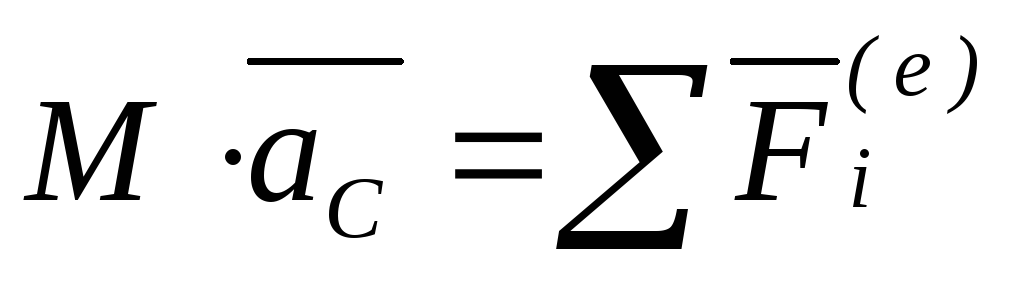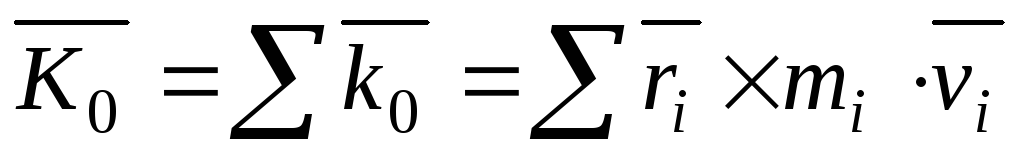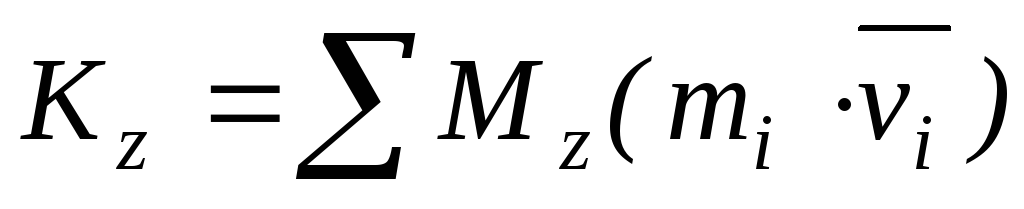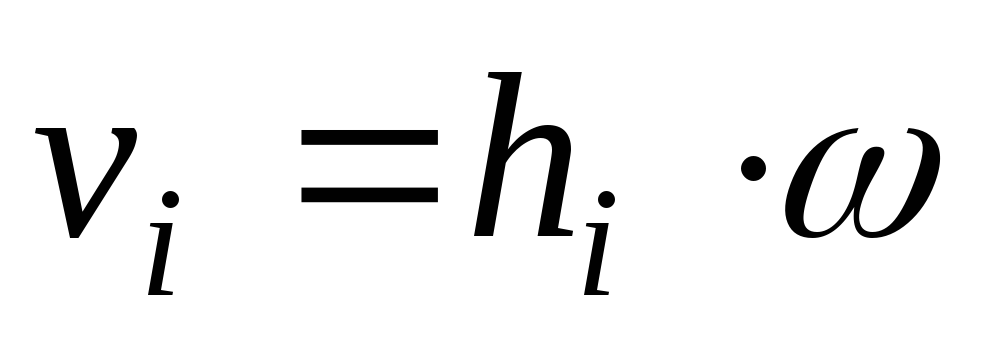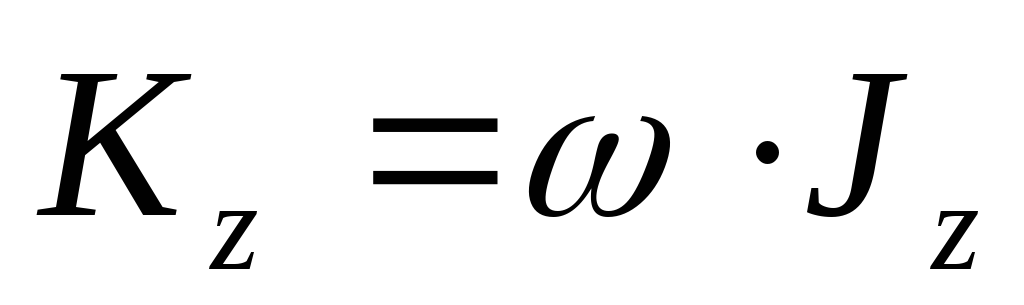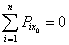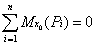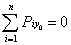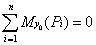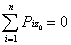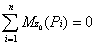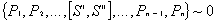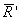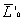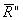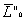Выведите закон сохранения количества движения

Из теоремы об изменении количества движения системы можно получить следующие важные следствия.

1. Пусть сумма всех внешних сил, действующих на систему, равна нулю:

Тогда из уравнения (20) следует, что при этом Таким образом, если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению.

2. Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например, ) равна нулю:

Тогда из уравнений (20) следует, что при этом Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения системы на эту ось есть величина постоянная.

Эти результаты и выражают закон сохранения количества движения системы. Из них следует, что внутренние силы изменить количество движения системы не могут. Рассмотрим некоторые примеры.

Явление отдачи или отката. Если рассматривать винтовку и пулю как одну систему, то давление пороховых газов при выстреле будет силой внутренней. Эта сила не может изменить количество движения системы, равное до выстрела кулю. Но так как пороховые газы, действуя на пулю, сообщают ей некоторое количество движения, направленное вперед, то они одновременно должны сообщить винтовке такое же количество движения в обратном направлении. Это вызовет движение винтовки назад, т. е. так называемую отдачу. Аналогичное явление получается при стрельбе из орудия (откат).

Работа гребного винта (пропеллера). Винт сообщает некоторой массе воздуха (или воды) движение вдоль оси винта, отбрасывая эту массу назад. Если рассматривать отбрасываемую массу и самолет (или судно) как одну систему, то силы взаимодействия винта и среды, как внутренние, не могут изменить суммарное количество движения этой системы. Поэтому при отбрасывании массы воздуха (воды) назад самолет (или судно) получает соответствующую скорость движения вперед, такую, что общее количество движения рассматриваемой системы остается равным нулю, так как оно было нулем до начала движения.

Аналогичный эффект достигается действием весел или гребных колес

Реактивное движение. В реактивном снаряде (ракете) газообразные продукты горения топлива с большой скоростью выбрасываются из отверстия в хвостовой части ракеты (из сопла ракетного двигателя). Действующие при этом силы давления будут силами внутренними и не могут изменить количество движения системы ракета — продукты горения топлива. Но так как вырывающиеся газы имеют известное количество движения, направленное назад, то ракета получает при этом соответствующую скорость, направленную вперед. Величина этой скорости будет определена в § 114.

Обращаем внимание на то, что винтовой двигатель (предыдущий пример) сообщает объекту, например самолету, движение за счет отбрасывания назад частиц той среды, в которой он движется. В безвоздушном пространстве такое движение невозможно. Реактивный же двигатель сообщает движение за счет отброса назад масс, вырабатываемых в самом двигателе (продукты горения). Движение это в равной мере возможно и в воздухе, и в безвоздушном пространстве.

При решении задач применение теоремы позволяет исключить из рассмотрения все внутренние силы. Поэтому рассматриваемую систему надо стараться выбирать так, чтобы все (или часть) заранее неизвестных сил сделать внутренними.

Закон сохранения количества движения удобно применять в тех случаях, когда по изменению поступательной скорости одной части системы надо определить скорость другой части. В частности, этот закон широко используется в теории удара.

Задача 126. Пуля массой , летящая горизонтально со скоростью и, попадает в установленный на тележке ящик с песком (рис 289). С какой скоростью начнет двигаться тележка после удара, если масса тележки вместе с ящиком равна

Решение. Будем рассматривать пулю и тележку как одну систему Это позволит при решении задачи исключить силы, которые возникают при ударе пули о ящик. Сумма проекций приложенных к системе внешних сил на горизонтальную ось Ох равиа нулю. Следовательно, или где — количество движения системы до удара; — после удара.

Так как до удара тележка неподвижна, то .

После удара тележка и пуля движутся с общей скоростью, которую обозначим через v. Тогда .

Приравнивая правые части выражений , найдем

Задача 127. Определить скорость свободного отката орудия, если вес откатывающихся частей равен Р, вес снаряда , а скорость снаряда по отношению к каналу ствола равна в момент вылета .

Решение. Для исключения неизвестных сил давления пороховых газов рассмотрим снаряд и откатывающиеся части как одну систему.

Пренебрегая за время движения снаряда в канале ствола сопротивлением откату и силами , которые очень малы по сравнению с силами давления пороховых газов, вызывающих откат, найдем, что сумма приложенных к системе внешних сил равна нулю (рис. 290; откатывающиеся вместе со стволом части на нем не показаны). Тогда , а так как до выстрела система неподвижна то и в любой момент времени

Обозначим скорость откатывающихся частей в конечный момент через v. Тогда абсолютная скорость снаряда в этот момент равна Следовательно,

Если бы была известна абсолютная скорость вылета снаряда то в равенство (а) вместо вошла бы сразу величина откуда

Знак минус в обоих случаях указывает, что направление v противоположно и.

Подчеркиваем, что при вычислении полного количества движения системы иадо учитывать абсолютные скорости движения ее частей.

Источник

Закон сохранения количества движения пример. Закон сохранения количества движения формула

Что такое закон сохранения количества движения?

Закон сохранения количества движения рассмотрим на примере.

Закон сохранения количества движения пример

Пусть имеется изолированная система двух тел с массами m₁ и m₂. В течении времени Δt тела взаимодействуют. На тело m₁ действует сила F₁ со стороны тела m₂. На тело m₂ действует сила F₂ со стороны тела m₁.

где u₁ — скорость тела m₁ после взаимодействия с телом m₂.

где u₂ — скорость тела m₂ после взаимодействия с телом m₁.

Выражаем импульсы сил через количества движений, подставляя правые части соответствующих формул:

Группируем количества движений до и после взаимодействий:

Из полученной формулы видно, что количество движения системы двух тел не изменилось.

Если изолированная система тел состоит из более чем двух тел, то тела попарно взаимодействуют и, проводя рассуждения для каждой пары, приходим к выводу, что количество движения изолированной системы потоянно при любом числе элементов этой системы.

Формулировка закона сохранения количества движения

Формулировка закона сохранения количества движения:

Формула закона сохранения количества движения

Формула закона сохранения количества движения для случая наличия только двух тел в системе:

А как изменить количество движения изолированной системы тел? Если подействовать на такую систему внешней силой или силами, то количество движения системы измениться, но только при условии, что сумма импульсов этих внешних сил отлична от нуля.

Источник

Законы сохранения количества движения.

1. Если главный вектор всех внешних сил системы равен нулю (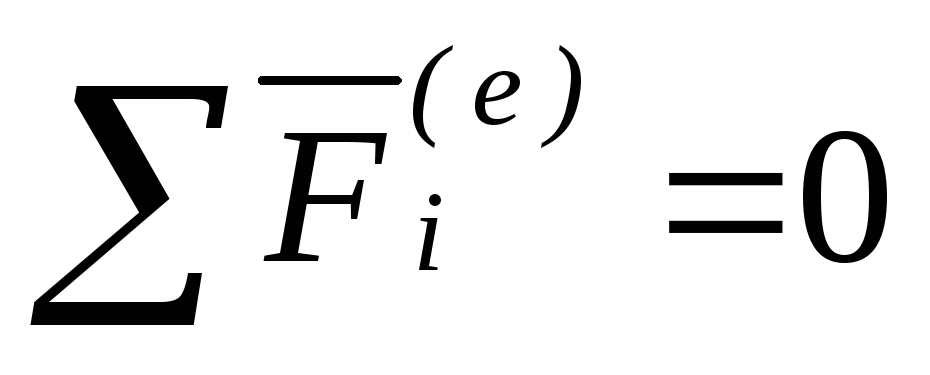), то количество движения системы постоянно по величине и направлению.

2. Если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю (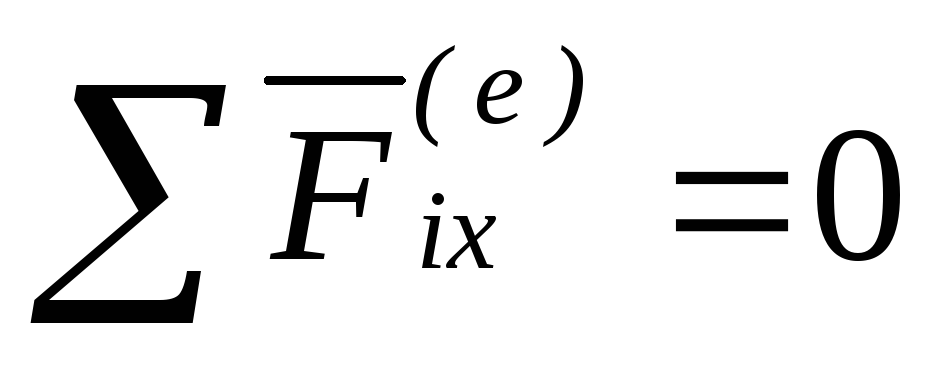), то проекция количества движения системы на эту ось является постоянной величиной.

Теорема о движении центра масс.

Теорема Центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к рассматриваемой механической системе.

, следовательно

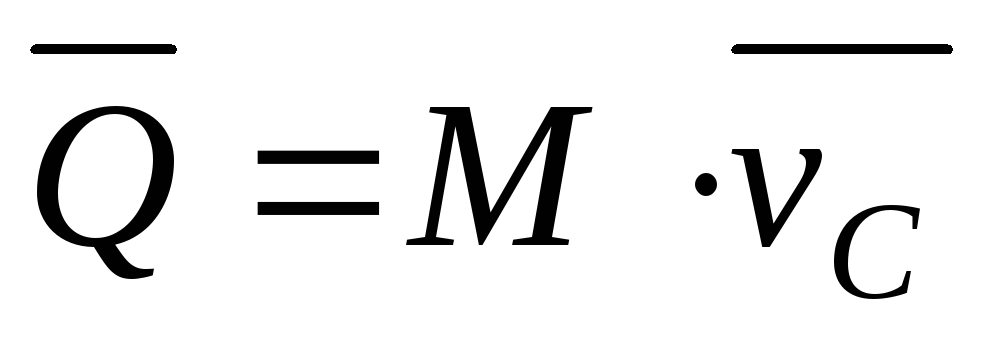
Момент количества движения системы.

Моментом количества движениясистемы материальных точек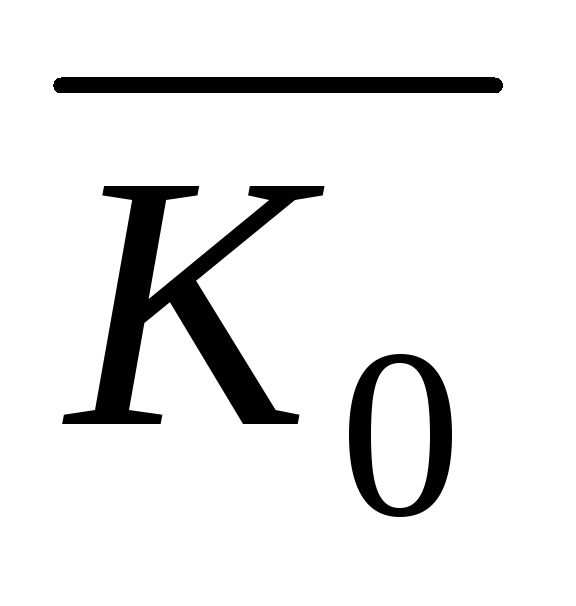относительно некоторого центраназывается векторная сумма моментов количества движения отдельных точек этой системы относительно того же центра

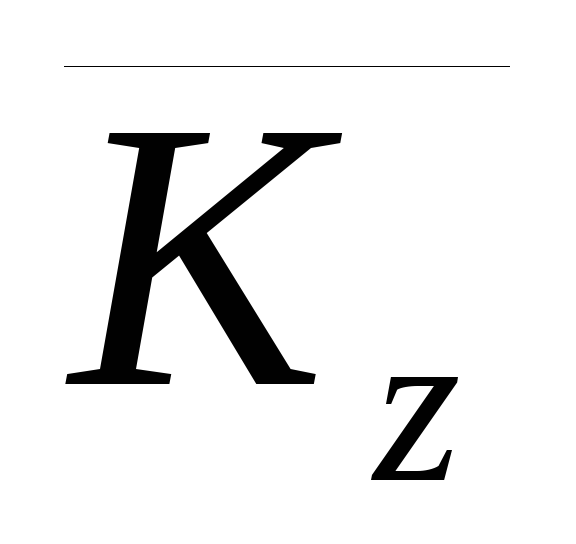
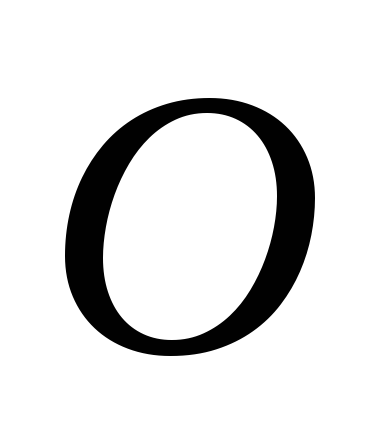
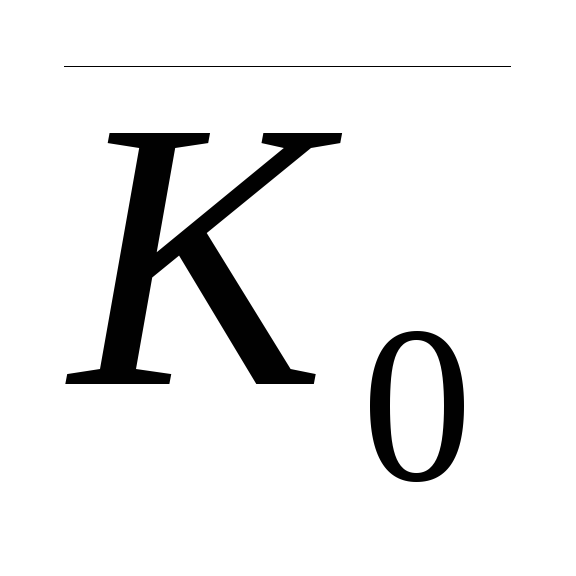
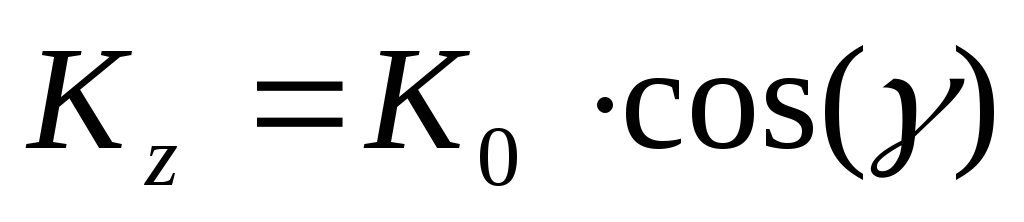
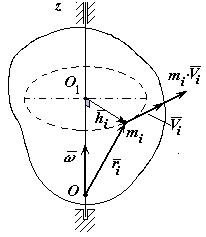
Моментом количества движениясистемы материальных точекотносительно какой-либо оси, проходящей через центр, называется проекция вектора количества движенияна эту ось.

Момент количества движения твердого тела относительно оси вращения при вращательном движении твердого тела.

Вычислим момент количества движения твердого тела относительно оси вращения.

Момент количества движения твердого тела относительно оси вращения при вращательном движении равен произведению угловой скорости тела на его момент инерции относительно оси вращения.

Теорема об изменении момента количества движения системы.

Теорема.Производная по времени от момента количества движения системы, взятого относительно какого-нибудь центра, равна векторной сумме моментов внешних сил, действующих на систему относительно того же центра.

(6.3)

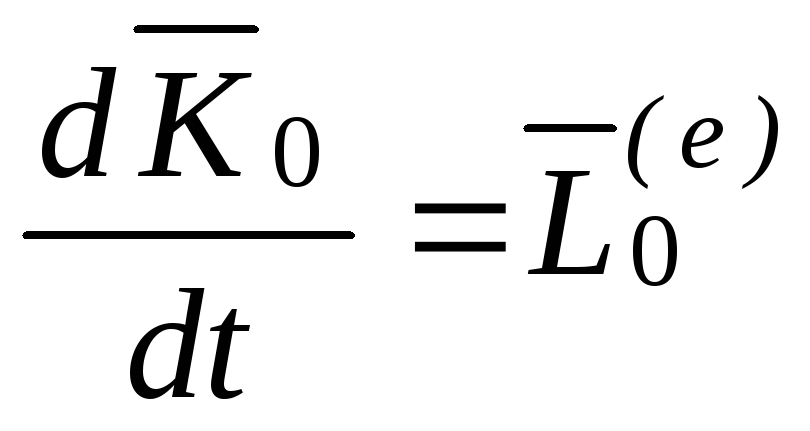
Доказательство: Теорема об изменении момента количества движения для точки имеет вид:

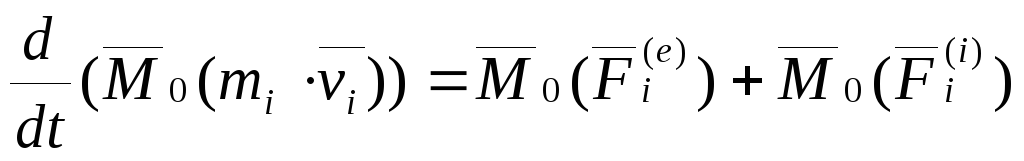
Сложим все уравнений и получим:

или ,

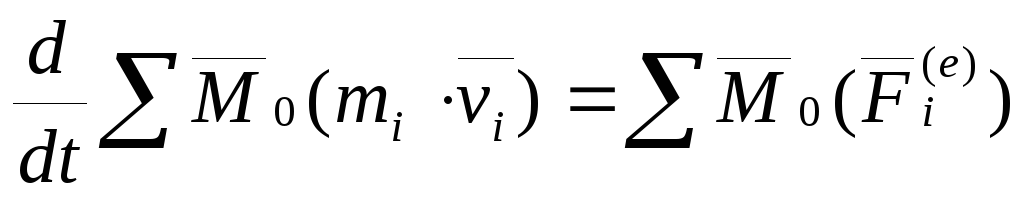
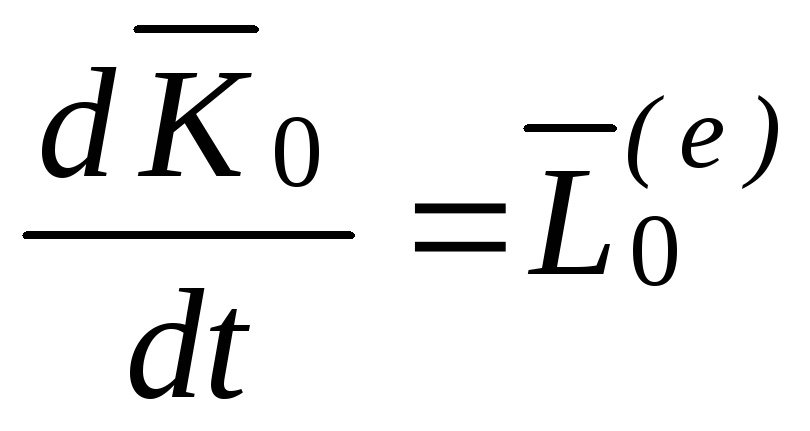
что и требовалось доказать.

Теорема.Производная по времени от момента количества движения системы, взятого относительно какой-либо оси, равна векторной сумме моментов внешних сил, действующих на систему относительно той же оси.

Для доказательства достаточно спроектировать векторное уравнение (6.3) на эту ось. Для оси это будет выглядеть так:.

(6.4)

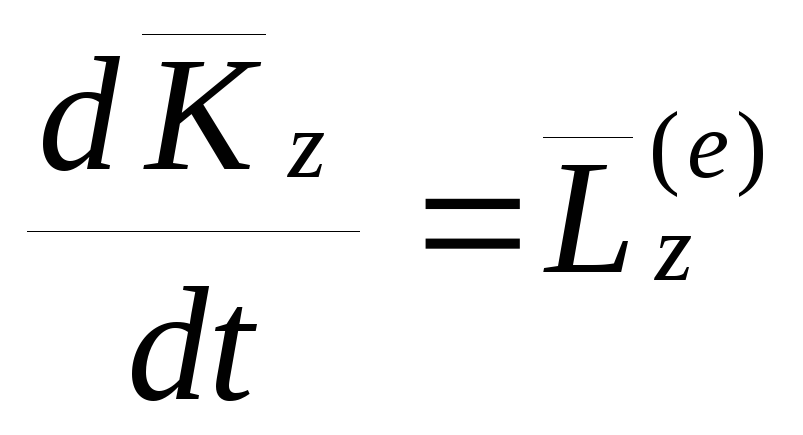
Теорема об изменении момента количества движения системы относительно центра масс. (без доказательства)

Для осей движущихся поступательно вместе с центром масс системы, теорема об изменении момента количества движения системы относительно центра масс сохраняет тот же вид, что и относительно неподвижного центра.

Модуль 2. Сопротивление материалов.

Тема 1 растяжение-сжатие, кручение, изгиб.

Деформации рассматриваемого тела (элементов конструкции) возникают от приложения внешней силы. При этом изменяются расстояния между частицами тела, что в свою очередь приводит к изменению сил взаимного притяжения между ними. Отсюда, как следствие, возникают внутренние усилия. При этом внутренние усилия определяются универсальным методом сечений (или метод разреза).

Известно, что различают силы внешние и силы внутренние. Внешние усилия (нагрузки) – это количественная мера взаимодействия двух различных тел. К ним относятся и реакции в связях. Внутренние усилия – это количественная мера взаимодействия двух частей одного тела, расположенных по разные стороны сечения и вызванные действием внешних усилий. Внутренние усилия возникают непосредственно в деформируемом теле.

На рис.1 приведена расчетная схема бруса с произвольной комбинацией внешней нагрузки образующую равновесную систему сил:

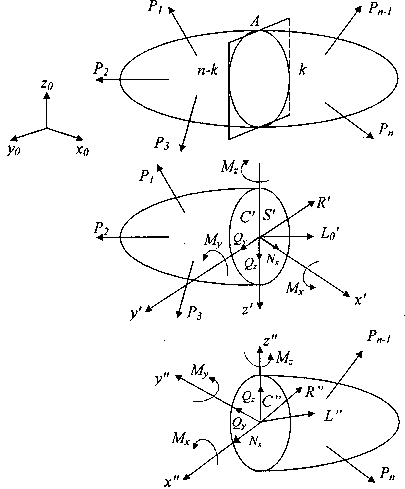
Сверху вниз: упругое тело, левая отсеченная часть, правая отсеченная частьРис.1. Метод сечений.

При этом, реакции связей определяются из известных уравнений равновесия статики твердого тела:

где х₀, у₀, z₀ — базовая система координат осей.

Мысленное разрезание бруса на две части произвольным сечением А (рис.1 a), приводит к условиям равновесия каждой из двух отсеченных частей (рис.1 б,в). Здесь <S’> и <S»>— внутренние усилия, возникающих соответственно в левой и правой отсеченных частях вследствие действия внешних усилий.

При составлении мысленно отсеченных частей, условие равновесия тела обеспечивается соотношением:

Так как исходная система внешних сил (1) эквивалентна нулю, получаем:

Это условие соответствует четвертой аксиоме статики о равенстве сил действия и противодействия.

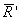
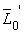
Используя общую методологию теоремы Пуансо о приведении произвольной системы сил к заданному центру и выбрав за полюс приведения центр масс, сечения А ‘ , точку С ‘ , систему внутренних усилий для левой части <S ’ > сводим к главному вектору и главному моментувнутренних усилий. Аналогично делается для правой отсеченной части, где положение центра масс сеченияА”; определяется, соответственно, точкой С» (рис.1 б,в).

Здесь в соответствие с четвертой аксиомой статики по-прежнему имеют место следующие соотношения:

Таким образом главный вектор и главный момент системы внутренних усилий, возникающие в левой, условно отсеченной части бруса, равны по величине и противоположны по направлению главному вектору и главному моменту системы внутренних усилий, возникающих в правой условно отсеченной части.

График (эпюра) распределения численных значений главного вектора и главного момента вдоль продольной оси бруса и предопределяют, прежде всего, конкретные вопросы прочности, жесткости и надежности конструкций.

Определим механизм формирования компонент внутренних усилий, которые характеризуют простые виды сопротивлений: растяжение-сжатие, сдвиг, кручение и изгиб.

В центрах масс исследуемых сечений С’ или С» зададимся соответственно левой (с’, х’, у’, z’) или правой (с», х», у», z”) системами координатных осей (рис.1 б, в), которые в отличие от базовой системы координат x, у, z будем называть «следящими». Термин обусловлен их функциональным назначением. 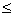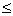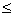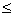А именно: отслеживание изменения положения сечения А (рис.1 а) при условном смещении его вдоль продольной оси бруса, например при: 0 х’₁ а, аx’₂ b и т.д., где а и b — линейные размеры границ исследуемых участков бруса.

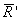
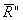
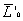
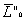
Зададимся положительными направлениями проекций главного вектора илии главного моментаилина координатные оси следящей системы (рис.1 б, в):

y, Q ’ _z> x, M ’ _y, M ’ _z>

y, Q ” _z> x, M ” _y, M ” _z>

При этом положительные направления проекций главного вектора и главного момента внутренних усилий на оси следящей системы координат соответствуют правилам статики в теоретической механике: для силы — вдоль положительного направления оси, для момента — против вращения часовой стрелки при наблюдении со стороны конца оси. Они классифицируются следующим образом:

N_x — нормальная сила, признак центрального растяжения или сжатия;

М_x — внутренний крутящий момент, возникает при кручении;

Q_z, Q_у — поперечные или перерезывающие силы – признак сдвиговых деформаций,

М_у, М_z — внутренние изгибающие моменты, соответствуют изгибу.

Соединение левой и правой мысленно отсеченных частей бруса приводит к известному (3) принципу равенства по модулю и противоположной направленности всех одноименных компонент внутренних усилий, а условие равновесии бруса определяется в виде:

С учетом эквивалентности нулю исходной системы сил (1) имеет место:

Как естественное следствие из соотношений 3,4,5 полученное условие является необходимым для того, чтобы одноименные компоненты внутренних усилий попарно образовали подсистемы сил эквивалентные нулю:

Источник