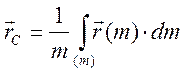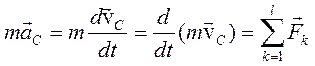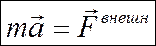Выведите закон сохранения импульса для системы материальных точек
§ 74. Теорема об изменении импульса системы материальных точек и закон сохранения импульса
1. Теорема об изменении импульса системы материальных точек.
Группу взаимодействующих тел называют системой тел.
Силы, с которыми тела системы взаимодействуют между собой, называют внутренними силами.
Все тела обладают массами, поэтому среди внутренних сил всегда есть сила тяготения. Между телами системы могут действовать силы упругости, электрические силы и тому подобное. Таким образом, внутренние силы могут быть как силами притяжения, так и силами отталкивания.
Согласно III закону Ньютона каждой силе действия есть сила противодействия, поэтому сумма внутренних сил взаимодействия всегда равна нулю.
Силы, с которыми внешние тела действуют на тела системы, называются внешними силами.
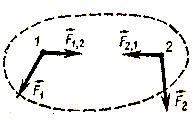
Для упрощения будем считать, что система состоит из двух тел.
По III закону Ньютона: 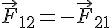
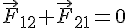
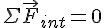
Запишем теорему об изменении импульса точки для каждого тела системы:
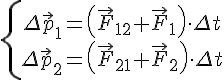
Сложим: 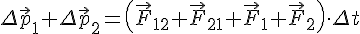
Получаем: 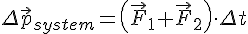
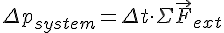
Теорема. Изменение импульса системы материальных точек прямо пропорционально сумме внешних сил, действующих на систему, и происходит в направлении действия суммарной силы.
Из теоремы вытекают два следствия.
Следствие 1. Внутренние силы не могут изменить импульса системы.
Следствие 2. Если сумма внешних сил равна нулю, то импульс системы не изменяется, т.е. сохраняется.
Если 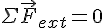
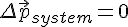
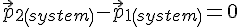
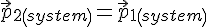
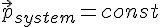
Второе следствие, открытое в механике на основе законов Ньютона, оказалось действующим на все явления Природы. Поэтому его стали называть законом сохранения импульса.
2. Закон сохранения импульса.
Если обозначить скорости тел системы до взаимодействия через 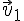
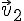
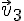
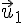
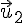
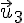
Система называется изолированной, или замкнутой, если на неё внешние силы не действуют.
Если сумма внешних сил, действующих на систему, равна нулю, или если система изолирована, то импульс системы сохраняется, т.е. сумма импульсов частиц до взаимодействия равна сумме импульсов частиц после взаимодействия.
Закон сохранения импульса можно применять:
1) когда сумма внешних сил равна нулю, или система изолирована;
2) если время взаимодействия очень мало (в этом случае силы не могут заметно изменить импульс системы, и его можно считать приближённо сохраняющимся);
3) вдоль того направления, по отношению к которому внешние силы действуют перпендикулярно (т.е. вдоль этого направления внешние силы не могут изменить импульса системы).
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
Источник
Закон сохранения импульса
Для вывода закона сохранения импульса рассмотрим некоторые понятия.
Механической системой называется совокупность материальных точек (тел), рассматриваемых как единое целое.
Внутренние силы – силы взаимодействия между материальными точками механической системы.
Внешние силы– силы, с которыми на материальные точки системы действуют внешние тела.
Замкнутой (изолированной) системой называется механическая система тел, на которую не действуют внешние силы.
Если имеется механическая система, состоящая из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т.е. геометрическая сумма внутренних сил равна нулю.
Вывод закона сохранения импульса
Рассмотрим механическую систему, состоящую из n тел, масса и скорости которых, соответственно, равны m1 , m2 , …, mnи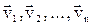
Пусть: 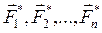
действующих на каждое из этих тел, а
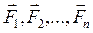
Запишем второй закон Ньютона для каждого из n тел механической системы:
Складывая эти уравнения почленно, получим:
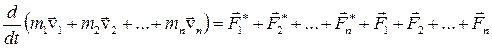
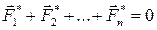
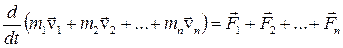
но т.к.
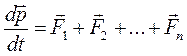
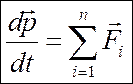
где 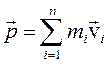
Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему. В случае отсутствия внешних сил – а именно так и есть в замкнутой механической системе производная по времени от импульса системы равна нулю. Это означает, что импульс замкнутой механической системы не изменяется, т.е. он постоянен:
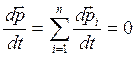
Последнее выражение и является законом сохранения импульса в замкнутой механической системе.
6. Центр масс системы материальных точек
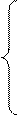
|
Центром масс (центр инерции) системы материальных точек является воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор определяется:
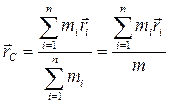
Частный случай: Если радиус-векторы проведены из центра масс С (обозначим их 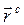
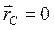
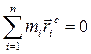
Таким образом, центр масс – это геометрическая точка, для которой сумма произведений масс всех материальных точек, образующих механическую систему, на их радиусы-векторы, проведенные из этой точки, равны нулю.
В случае непрерывного распределения массы в системе, радиус-вектор центра масс:
Закон движения центра масс:
Таким образом, центр инерции механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору внешних сил, приложенных к системе.
Если рассматриваемая система – твердое тело, которое движется поступательно, то скорости vi всех точек тела и его центра инерции vc одинаковы и равны v скорости тела; соответственно ускорение тела а = ас , и основное уравнение динамики имеет вид:
Этот закон показывает, что для изменения скорости ц.м. системы необходимо, чтобы на систему подействовала внешняя сила. Внутренние силы взаимодействия частей системы могут вызвать изменение скоростей этих частей (например, разрыв снаряда на несколько осколков), но они не могут повлиять на суммарный импульс системы и скорость ее центра масс.
Из закона движения центра масс следует, что скорость ц.м. замкнутой механической системы не изменяется с течением времени. Т.е. центр масс замкнутой системы либо покоится, либо движется с постоянной скоростью относительно инерциальной системы отсчета.
Строго говоря, замкнутых систем в природе нет, хотя бы уже потому, что на все тела действуют силы тяготения. Однако в практических целях для простоты расчетов некоторые механические системы можно считать замкнутыми, если силы взаимодействия частей такой системы во много раз больше внешних сил.
При небольших допущениях можно считать Солнечную систему замкнутой.
7. Движение тел переменной массы. Формула Мещерского
Примером тел переменной массы может служить вращающаяся катушка с кабелем, масса которой увеличивается или уменьшается в зависимости от того, наматывается на нее кабель или сматывается.
Типичным примером движения тел переменной массы может служить полет ракеты на активном участке траектории, т.к. в процессе работы ее двигателя топливо сгорает, а продукты сгорания выбрасываются через сопло. Масса ракеты, таким образом, постепенно уменьшается.
Изменение импульса тела переменной массы за время dt :
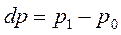
где 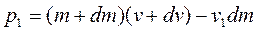
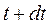
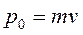
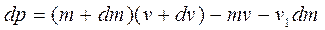
здесь: m и v – масса и скорость тела в момент времени t;
dm и dv – их изменения за малый промежуток времени dt;
v1 – скорость отделяющихся частиц.
Если частицы отделяются, то их общая масса dm
Источник
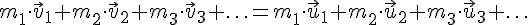
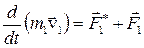
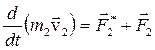
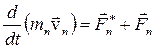
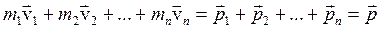
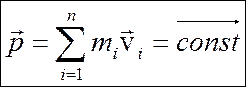
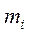 и
и 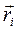 – масса и радиус-вектор i-той материальной точки; — n – число материальных точек в системе; —
– масса и радиус-вектор i-той материальной точки; — n – число материальных точек в системе; — 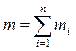 – масса системы.
– масса системы.