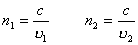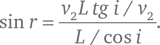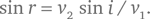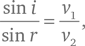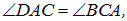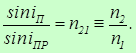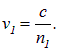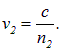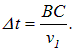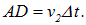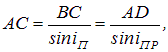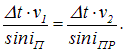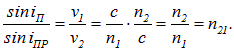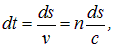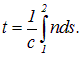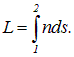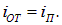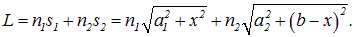Выведите закон преломления волн

Урок 3. ЗАКОН ПРЕЛОМЛЕНИЯ СВЕТА

Напомним, в чем состоит явление преломления света. Выведем закон преломления с помощью принципа Гюйгенса.

Наблюдение преломления света

На границе двух сред свет меняет направление своего распространения. Часть световой энергии возвращается в первую среду, т.е. происходит отражение света. Если вторая среда прозрачна, то свет частично может пройти через границу сред, также меняя при этом, как правило, направление распространения. Это явление называется преломлением света.

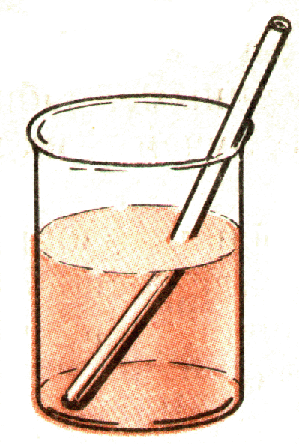
Вследствие преломления наблюдается кажущееся изменение формы предметов, их расположения и размеров. В этом нас могут убедить простые наблюдения. Положим на дно пустого не прозрачного стакана монету или другой небольшой предмет. Подвинем стакан так, чтобы центр монеты, край стакана и глаз находились на одной прямой. Не меняя положения головы, будем наливать в стакан воду. По мере повышения уровня воды дно стакана с монетой как бы приподнимается. Монета, которая ранее была видна лишь частично, теперь будет видна полностью. Установим наклонно карандаш в сосуде с водой. Если посмотреть на сосуд сбоку, то можно заметить, что часть карандаша, находящаяся в воде, кажется сдвинутой в сторону (рис. 5).

Эти явления объясняются изменением направления лучей на границе двух сред — преломлением света.

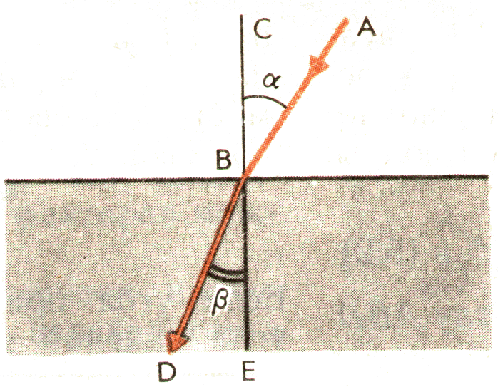
Закон преломления света определяет взаимное расположение падающего луча АВ (рис. 6), преломленного DB и перпендикуляра СЕ к поверхности раздела сред, восставленного в точке падения. Угол a называется углом падения, а угол b — углом преломления.

Падающий, отраженный и преломленный лучи нетрудно наблюдать, сделав узкий световой пучок видимым. Ход такого пучка в воздухе можно проследить, если пустить в воздух немного дыма или же поста­вить экран под небольшим углом к лучу. Преломленный пучок также виден в подкрашенной флюоресцеином воде аквариума (рис. 7).

Вывод закона преломления света

Закон преломления света был установлен опытным путем в XVII веке. Мы его выведем с помощью принципа Гюйгенса.

Преломление света при переходе из одной среды в другую вызвано различием в скоростях распространения света в той и другой среде. Обозначим скорость волны в первой среде через u ₁, а во второй — через u ₂.

Пусть на плоскую границу раздела двух сред (например, из воздуха в воду) падает плоская световая волна (рис. 8).

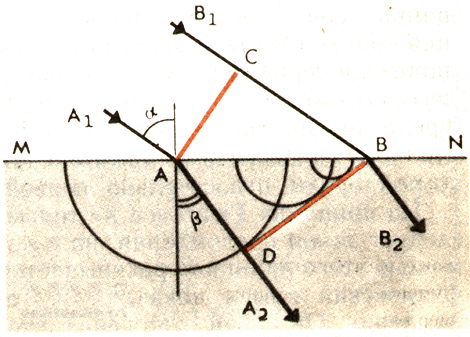Волновая поверхность АС перпендикулярна лучам А₁А и В₁В. Поверхности MN сначала достигнет луч А₁А. Луч В₁В достигнет поверхности спустя время

Поэтому в момент, когда вторичная волна в точке В только начнет возбуждаться, волна от точки А уже имеет вид полусферы радиусом AD= u ₂ ∆ t.

Волновую поверхность преломленной волны можно получить, проведя поверхность, касательную ко всем вторичным волнам во второй среде, центры которых лежат на границе раздела сред. В данном случае это плоскость BD. Она является огибающей вторичных волн.

Угол падения α луча равен углу CAB в треугольнике AВС (стороны одного из этих углов перпендикулярны сторонам другого). Следовательно,

Угол преломления β равен углу ABDтреугольника ABD. Поэтому

Разделив почленно (1.2) на (1.3), получим

(1.4)

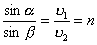
где n — постоянная величина, не зависящая от угла падения

Из построения (рис.8) видно, что падающий луч, луч преломленный и перпендикуляр, восставленный в точке падения, лежат в одной плоскости. Данное утверждение совместно с уравнением (1.4), согласно которому отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред, представляет собой закон преломления света.

Убедиться в справедливости закона преломления можно экспериментально, измеряя углы падения и преломления и вычисляя отношение их синусов при различных углах падения. Это отношение остается неизменным.

Постоянная величина, входящая в закон преломления света, называется относительным показателем преломления или показателем преломления второй среды относительно первой.

Из принципа Гюйгенса не только следует закон преломления, но с помощью этого принципа раскрывается физический смысл показателя преломления. Он равен отношению скоростей света в средах, на границе между которыми происходит преломление:

(1.5)

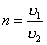
Если угол преломления β меньше угла падения α, то согласно (1.4) скорость света во второй среде меньше, чем в первой.

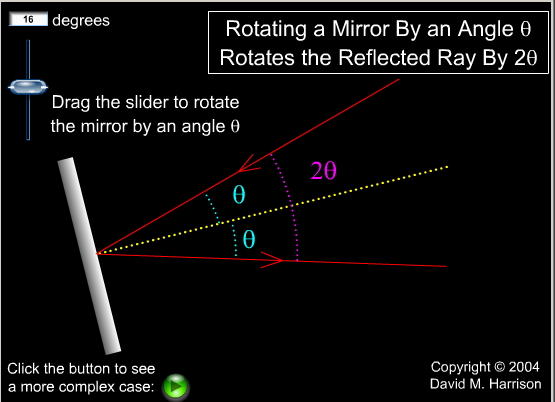
Показатель преломления среды относительно вакуума называют абсолютным показателем преломления этой среды. Он равен отношению синуса угла падения к синусу угла преломления при переходе светового луча из вакуума в данную среду.

Пользуясь формулой (1.5), можно выразить относительный показатель преломления через абсолютные показатели преломления п₁ и п₂ первой и второй сред.

Действительно, так как

где с — скорость света в вакууме, то

(1.6)

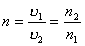
Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой.

Абсолютный показатель преломления определяется скоростью распространения света в данной среде, которая зависит от физического состояния среды, т. е. от температуры вещества его плотности, наличия в нем упругих напряжений. Показатель преломления зависит также и от характеристик самого света. Для красного света он меньше, чем для зеленого, а для зеленого — меньше, чем для фиолетового.

Поэтому в таблицах значений показателей преломления для разных веществ обычно указывается, для какого света приведено данное значение n и в каком состоянии находится среда. Если таких указаний нет, то это означает, что зависимостью от указанных факторов можно пренебречь.

В большинстве случаев приходится рассматривать переход света через границу воздух — твердое тело или воздух — жидкость, а не через границу вакуум — среда. Однако абсолютный показатель преломления п₂ твердого или жидкого вещества отличается от показателя преломления того же вещества относительно воздуха незначительно. Так, абсолютный показатель преломления воздуха при нормальных условиях для желтого света равен приблизительно п₁ » 1,000292. Следовательно,

(1.7)

Значения показателей преломления для некоторых веществ относительно воздуха приведены в таблице (данные относятся к желтому свету).

Источник

Вывод закона преломления света на основе волнового принципа

Закон преломления света можно вывести, исходя из предположения о том, что свет движется по пути наименьшего времени, как было описано в техническом замечании 28. Но его также можно вывести и на основе волновой теории света. По мнению Гюйгенса, свет – это колебания какой‑то среды, которая может либо быть заполнена прозрачной материей, либо представляться нам пустотой. Фронт возмущения этой среды являет собой прямую линию, которая движется вперед в направлении своего перпендикуляра со скоростью, характерной для среды, в которой он распространяется.

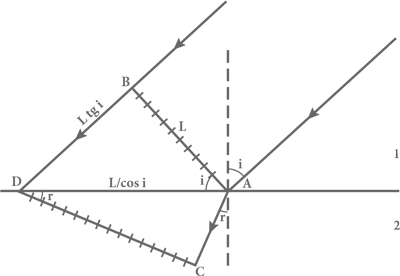
Рис. 23. Преломление световой волны. И снова горизонтальная линия обозначает границу раздела двух прозрачных сред, в которых свет движется с разными скоростями. Отрезки с поперечными штрихами обозначают фронт волны в разные момены времени – когда передний край фронта волны входит в контакт с границей и когда задний край теряет контакт с границей. Прямые линии со стрелками указывают траектории перемещения переднего и заднего края волнового фронта.

Рассмотрим сегмент такого фронта возмущения длиной L в среде 1, который движется по направлению к границе со средой 2. Допустим, что направление его движения, совпадающее с перпендикуляром к фронту волны, образует с нормалью (перпендикуляром) к этой границе угол i . Когда передний край фронта касается границы раздела сред в точке A , задний его край B еще находится на некотором расстоянии (измеряемом вдоль направления движения волны) от границы, равном L tg i (см. рис. 23). Это значит, что теперь задняя граница фронта волны достигнет пограничной точки D через промежуток времени, равный L tg i /v ₁, где v ₁ – скорость распространения возмущения в среде 1. В течение того же времени передний край фронта возмущения будет перемещаться в среде 2 под углом r от перпендикуляра к границе раздела сред к точке C , которая расположена на расстоянии v ₂L tg i /v ₁, где v ₂ – скорость распространения возмущения в среде 2. Когда он пройдет этот путь, волновой фронт, расположенный под прямым углом к направлению своего движения в среде 2, протянется между точками C и D , образуя таким образом прямоугольный треугольник с вершинами A, С и D , в котором угол при вершине C прямой.

Катет AC длиной v ₂L tg i /v ₁ – противолежащий углу r в этом треугольнике. Его гипотенуза – отрезок AD , имеющий длину L /cos i (см. рис. 23). Отсюда:

Вспомнив, что tg i = sin i /cos i , замечаем, что множители cos i и L сокращаются, оставляя:

Или, если выразить это иначе,

что и является формулой закона преломления света.

То, что волновая теория света, как доказал Гюйгенс, описывает явление преломления так же, как и принцип наименьшего времени следования, описанный Ферма, вовсе не случайно. Можно показать, что даже в том случае, когда волна движется сквозь неоднородную среду, в которой скорость светового луча плавно меняется в различных направлениях, а не резко на границе раздела сред, из волновой теории Гюйгенса следует, что луч между двумя точками всегда будет следовать по пути наименьшего времени.

Дата добавления: 2016-01-29 ; просмотров: 1850 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

3.2. Законы отражения и преломления света

Корпускулярная теория очень просто объясняла явления геометрической оптики, описываемые в терминах распространения световых лучей. С точки зрения волновой теории, лучи — это нормали к фронту волны. Принцип Гюйгенса также позволяет объяснить законы геометрической оптики на основе волновых представлений о природе света.

Закон отражения

Когда световые волны достигают границы раздела двух сред, направление их распространения изменяется. Если они остаются в той же среде, то происходит отражение света.

Отражение света — это изменение направления световой волны при падении на границу раздела двух сред, в результате чего волна продолжает распространяться в первой среде.

Закон отражения света хорошо известен:

Падающий луч, перпендикуляр к границе раздела двух сред в точке падения и отраженный луч лежат в одной плоскости, причем угол падения равен углу отражения.

Направления распространения падающей и отраженной волн показаны на рис. 3.2.

Рис. 3.2. Отражение света от плоской поверхности

Закон отражения может быть выведен из принципа Гюйгенса. Действительно, допустим, что плоская волна, распространяющаяся в изотропной среде, падает на границу раздела двух сред АС (рис. 3.3).

Рис. 3.3. Применение принципа Гюйгенса к выводу закона отражения

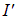
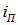
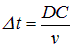
Достаточно рассмотреть два параллельных луча I и в падающем пучке. Углом падения называют угол между нормалью п к поверхности раздела и падающим лучом I. Плоский фронт AD падающей волны сначала достигнет границы раздела двух сред в точке А, которая станет источником вторичных волн. Согласно принципу Гюйгенса, из нее, как из центра, будет распространяться сферическая волна. Через время

,

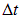
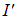
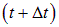
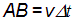
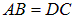
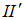
то есть с запаздыванием во времени на , луч из падающего пучка придет в точку С, которая в этот момент времени также станет источником вторичной волны. Но, к этому моменту вторичная сферическая волна, распространяющаяся из точки А, уже будет иметь радиус (как и должно быть: ). Мы знаем теперь положение двух точек фронта отраженной волны — С и В. Чтобы не загромождать рисунок, мы не показываем вторичных волн, испущенных точками между А и С, но линия CD будет касательной (огибающей) ко всем из них. Стало быть, CВ действительно является фронтом отраженной волны. Направление ее распространения (лучи II и ) ортогонально фронту CD. Из равенства треугольников ABC и ADC вытекает равенство углов

что, в свою очередь, приводит к закону отражения

На рис. 3.4 представлена интерактивная модель отражения света.

Рис. 3.4. Изучение закона отражения света

Закон преломления

Если световые волны достигают границы раздела двух сред и проникают в другую среду, то направление их распространения также изменяется — происходит преломление света.

Преломление света — это изменение направления распространения световой волны при переходе из одной прозрачной среды в другую.

Направление распространения падающей и преломленной волны показано на рис. 3.5.

Рис. 3.5. Преломление света на плоской границе раздела двух прозрачных сред

Закон преломления гласит:

Падающий луч, перпендикуляр к границе раздела сред в точке падения и преломленный луч лежат в одной плоскости, причем отношение синуса угла падения к синусу угла преломления постоянно для данной пары сред и равно показателю преломления второй среды относительно первой

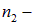
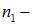
Здесь показатель преломления среды, в которой распространяется преломленная волна, показатель преломления среды, в которой распространяется падающая волна.

Закон отражения также вытекает из принципа Гюйгенса. Рассмотрим (рис. 3.6) плоскую волну (фронт АВ), которая распространяется в среде с показателем преломления 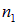, вдоль направления I со скоростью

Эта волна падает на границу раздела со средой, в которой показатель преломления равен 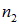, а скорость распространения

Рис. 3.6. К выводу закона преломления света с помощью принципа Гюйгенса

Время, затрачиваемое падающей волной для прохождения пути ВС, равно

За это же время фронт вторичной волны, возбуждаемой в точке А во второй среде, достигнет точек полусферы с радиусом

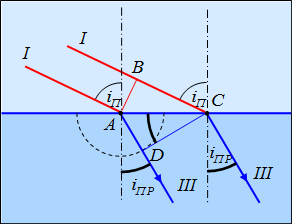
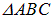
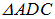
В соответствии с принципом Гюйгенса положение фронта преломленной волны в этот момент времени задается плоскостью DC, а направление ее распространения — лучом III, перпендикулярным к DC. Из треугольников и следует

Таким образом, закон преломления света записывается так:

На рис. 3.7 представлена интерактивная модель преломления света на границе раздела двух сред.

Рис. 3.7. Изучение закона преломления

Для еще одной иллюстрации применения принципа Гюйгенса рассмотрим пример.

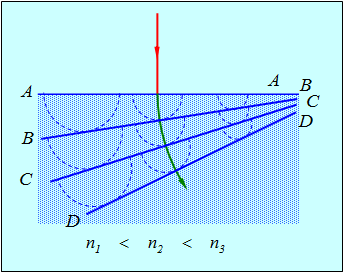
Пример. На плоскую границу раздела двух сред падает нормально луч света. Показатель преломления среды непрерывно увеличивается от ее левого края к правому (рис. 3.8). Определим, как будет идти луч света в этой неоднородной среде.

Рис. 3.8. Искривление луча света в неоднородной среде

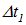
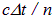
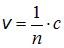
Пусть фронт волны АА подошел к границе раздела сред. Точки раздела сред можно рассматривать как центры вторичных волн. Через время испущенные вторичные сферические волны достигают точек на расстоянии от фронта АА. Поскольку показатель преломления среды растет слева направо, эти расстояния убывают слева направо. Огибающая к вторичным волнам — новый фронт ВВ — повернется. Если теперь взять точки фронта ВВ за источники вторичных волн, то за время они породят волны, образующие фронт СС. Он еще более повернут. Его точки порождают фронт DD и т. д. Проводя нормаль к волновым фронтам в разные моменты времени, получаем путь светового луча в среде с переменным показателем преломления (зеленая линия). Видно, что луч искривляется в сторону увеличения показателя преломления. Аналогия: если притормозить левые колеса автомобиля, его повернет налево. Для света степень «торможения» растет с ростом показателя преломления среды: .

Эта задача имеет отношение к явлению, наблюдающемуся на море. Когда ветер дует с берега, иногда возникает так называемая «зона молчания»: звук колокола с судна не достигает берега. Обычно говорят, что звук относится ветром. Но даже при сильном урагане скорость ветра примерно в 10 раз меньше скорости звука, так что «отнести» звук ветер никак не может. Объяснение заключается в том, что скорость встречного ветра у поверхности моря вследствие трения меньше, чем на высоте. Поэтому скорость звука у поверхности больше, и линия распространения звука загибается кверху, не попадая на берег.

http://www.nvtc.ee/e-oppe/Sidorova/objects/index.html – Законы преломления, отражения света. Зеркала. Теория и примеры задач. В «Итоговых заданиях» — кроссворд.

http://publ.lib.ru/ARCHIVES/B/. – Тарасов Л.В., Тарасова А.Н., «Беседы о преломлении света».

Принцип Ферма.

Итак, волновая оптика способна объяснить явления отражения и преломления света столь же успешно, как и геометрическая оптика. В основу последней, трактующей явления на основе законов распространения лучей, положен принцип Ферма:

Свет распространяется по такому пути, для прохождения которого требуется минимальное время.

Для прохождения участка пути 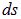свету требуется время

где v=с/п — скорость света в среде. Таким образом, время t, затрачиваемое светом на путь от точки 1 до точки 2, равно

Введем величину с размерностью длины, которая называется оптической длиной пути:

Пропорциональность t и L позволяет сформулировать принцип Ферма следующим образом:

Свет распространяется по такому пути, оптическая длина которого минимальна.

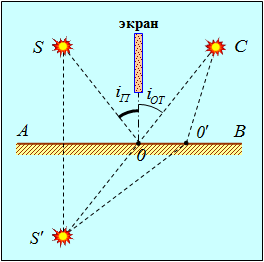
Рассмотрим путь света из точки S в точку С после отражения от плоскости АВ (рис. 3.9).

Рис. 3.9. Применение принципа Ферма к отражению света

Непосредственное попадание света из S в С невозможно из-за экрана. Нам надо найти точку О, отразившись в которой луч попадет в точку С. Среда, в которой проходит луч, однородна. Поэтому минимальность оптической длины пути сводится к минимальности его геометрической длины. Рассмотрим зеркальное изображение S’ точки S. Геометрические длины путей SOC и S’OC равны. Поэтому минимальность длины SOC эквивалентна минимальности длины S’OC. А минимальная геометрическая длина пути из S’ в С будет соответствовать прямой, соединяющей точки S’ и С. Пересечение этой прямой с плоскостью раздела сред дает положение точки О. Отсюда следует равенство углов:

то есть закон отражения света.

Рассмотрим теперь явление преломления света (рис. 3.10).

Рис. 3.10. Применение принципа Ферма к преломлению света

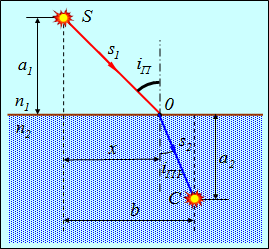
Определим положение точки О, в которой должен преломиться луч, распространяясь от S к С, чтобы оптическая длина пути L была минимальна. Выражение для L имеет вид

Найдем величину х, соответствующую экстремуму оптической длины пути:

Источник