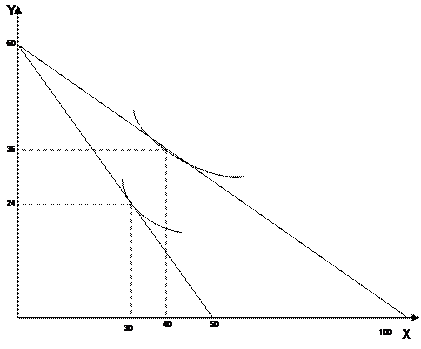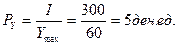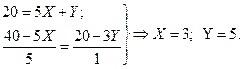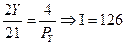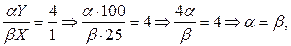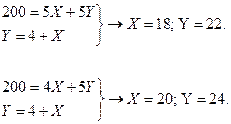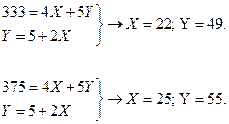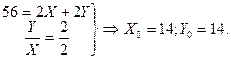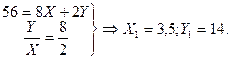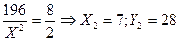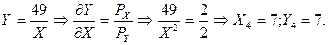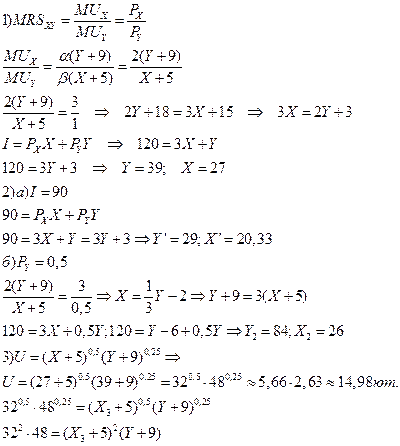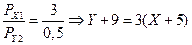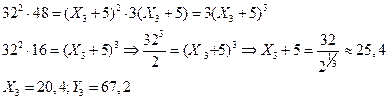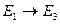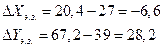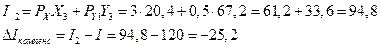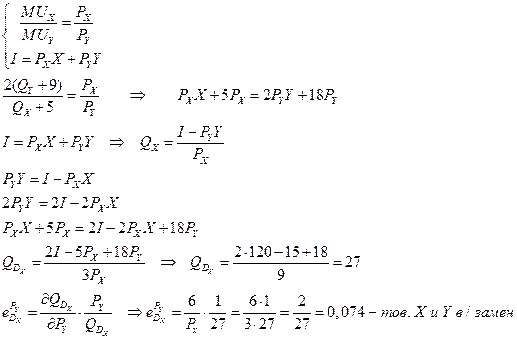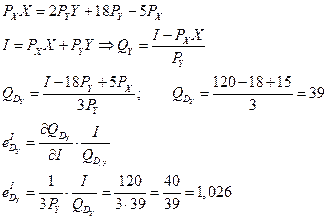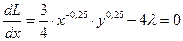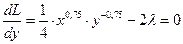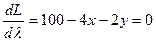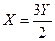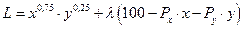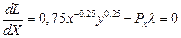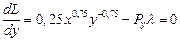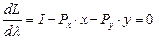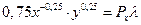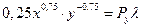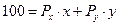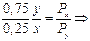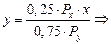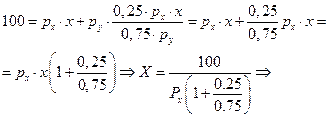Выведите уравнение линии доход потребление

Примеры решений задач: функция полезности

В этом разделе вы найдете подробно решенные задачи, касающиеся функции полезности, задачи выбора потребителем набора благ при заданном бюджетном ограничении, максимизации полезности, заменяемости товаров и т.д.

Функция полезности: задачи с решениями

Задача 1. Функция полезности имеет вид: $TU=4xy$, где X и Y — количество товаров. Расходы потребителя на эти два товара в месяц равны 1200 р., цена товара X — 400 р., товара Y — 300 р. Определите оптимальный объем ежемесячных закупок двух данных товаров и соответствующее ему значение общей полезности.

Задача 2. Условия: потребитель расходует 200 руб. в неделю на покупку товаров А и В.
Цена (руб.) Кол-во покупаемых единиц товаров Общая полезность Предельная полезность
А 7 20 500 20
В 5 12 1000 30
Задание: Объяснить, как должен поступать потребитель, чтобы максимизировать получаемую полезность при данном бюджете.

Задача 3. Потребитель покупает три товара Х, Y, Z, цены которых соответственно равны Px=100 руб.; Py=70 руб.; Pz=50 руб. Функции общей полезности разных благ: $F(TU(x))=3\sqrt$, $F(TU(y))=5\sqrt$, $F(TU(z))=5\sqrt$.
Определить:
1) каким образом потребитель может использовать денежный запас 500 рублей для достижения максимальной полезности при потреблении и рассчитать её количественно;
2) то же, если при покупке более, чем 2-х товаров Px снижается на 25%, а Py – на 50%

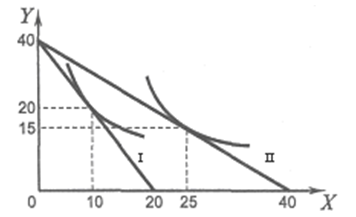
Задача 4. Допустим, потребитель имеет доход 200 ден. ед. На рисунке показаны две бюджетные линии (I и II) и соответствующие им кривые безразличия.

Определить координаты (P,Q) двух точек линии спроса данного потребителя на товар Х.

Задача 5. Общая полезность благ $\alpha$ и $\beta$ для некоего потребителя описывается уравнениями $U_\alpha = q_\alpha(15 — 0,5q_\alpha)$, $U_\beta = q_\beta(30 — q_\beta)$. Допустим, потребитель располагает бюджетом для покупки $\alpha$ и $\beta$ в размере 120 руб., цены на $\alpha$ и $\beta$ равны соответственно 5 и 10 руб. Определить количество $\alpha$ и $\beta$, максимизирующее полезность потребителя.

Задача 6. Потребитель тратит 7 долларов в день на товары X и Y. MU товара X для него равна $10 – x$, где $x$ — количество X в шт. MU товара Y: $21 – 2y$, где $y$ — количество Y в шт. Р 1 ед. товара X = 1 доллар, P 1 ед. Y = 1 доллар. Какое количество X и Y купит рациональный покупатель?

Задача 7. В таблице представлена предельная полезность для походов в магазин.
Имея 100 руб. 80 коп. потребитель купил 3 буханки хлеба по цене 8 руб. за буханку, 4 пакета молока по 11 руб. 20 коп. за пакет и 2 пачки сахара по 16 руб. за пачку. Достиг ли он максимума полезности? Ответ обосновать и в случае отрицательного ответа определить объем покупок, обеспечивающий максимум полезности при данном бюджете.

Задача 8. Построить кривую безразличия для двух абсолютно взаимозаменяемых товаров: пепси-колы и кока-колы, если их цены за литр равны 8 и 10 ден. ед. при бюджете на их потребление, равном 40 ден. ед.

Задача 9. Индивидуум имеет функцию полезности типа Неймана—Моргенштерна, а элементарная функция полезности строго возрастает и зависит только от одного аргумента (денег). Лотерея 6 долларов и 10 долларов с вероятностями 1/3 и 2/3 и лотерея 3 доллара и 9 долларов с вероятностями 2/3 и 1/3 для него эквивалентны. Что можно сказать о склонности данного индивида к риску?

Задача 10. Пусть функция полезности наборов из двух товаров $X=(x_1,x_2)$ имеет вид $u(x_1,x_2)=x_1^<1>x_2^<1>$.
• Найти набор товаров, который имеет такую же полезность, как набор $X_1=(5,3)$ и количество второго товара равно 1.
• Для набора $X_1=(5,3)$ найти предельные полезности первого и второго товаров.
• В наборе $X_1=(5,3)$ количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.

Задача 11. Функция полезности потребителя имеет вид $u(x_1,x_2)=(x_1-50)^<1>(x_2-40)^<1>$.
1. Найти равновесный спрос и его полезность, если рыночная цена первого товара $p_1=5$, рыночная цена второго товара $p_2=3$ и потребитель выделяет на приобретение товаров сумму $M=5000$ денежных единиц.
2. Найти функции спроса на оба вида товаров.
3. Найти спрос на оба товара при увеличении дохода на 30 денежных единиц и при уменьшении дохода на 60 денежных единиц.

Задача 12. Для потребителя с функцией полезности $U(x_1,x_2)=x_1^<1>x_2^<1>$
1) найдите функцию спроса на каждый товар;
2) найдите точку спроса при доходе $K=60$ и ценах $P=(2,4)$.

Задача 13. Решить прямую задачу потребителя (найти оптимальную потребительскую корзину). Дано: Функция полезности потребителя $U=\sqrt$. Цена блага х равна 15, цена блага у равна 20, доход потребителя равен 300.
Найти: Оптимальный набор благ потребителя $(х, у)$.

Задача 14. Предельная полезность первой единицы блага равна 300. При потреблении первых трех единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза. Предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 5 раз. Найти совокупную полезность 5 единиц блага.

Источник

Порядковый подход к анализу полезности и спроса

№ 3. Допустим, потребитель имеет доход 300 ден. ед. На рисунке показаны две бюджетные линии и соответствующие им кривые безразличия:

Рис. 1.1. Оптимум потребителя.

1. Какова цена товара Y?

2. Определите координаты двух точек линии спроса данного потребителя на товар X.

3. Зависит ли положение данной линии спроса от цены товара Y, от дохода потребителя?

Решение:

1.

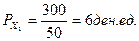
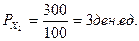
2. При , Х₁= 30 и при , Х₂=40

3. Зависит от P_Y и от I. В бюджетном ограничении все величины взаимосвязаны: I = P_X X + P_Y Y.

№ 4. Предельная полезность X для индивида отображается функцией MU_Х = 40 – 5Х, а предельная полезность Y, MU_Y = 20 – 3Y. Известны цены благ и доход индивида: P_Х = 5; P_Y = 1; I= 20. Какое количество каждого из благ должен купить индивид для максимизации общей полезности?

Решение:

Потребитель получит максимум полезности, если распределит свой бюджет: I = P_Х Х+ P_YY, так, что MU_Х/P_Х = MU_Y/P_Y. Получаем систему из двух уравнений:

№ 5. Функция полезности индивида имеет вид: 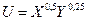; при имеющемся у него бюджете он купил 21 ед. блага Х по цене Р_Х = 4, а оставшиеся деньги потратил на покупку блага Y.

Определить:

1. Бюджет индивида;

2. Сколько единиц блага Y купит данный индивид, если Р_Y = 7?

Решение:

1. Система из двух уравнений:

MU_Х/ MU_Y = P_X /P_Y

по условию задачи принимает вид:

2. На приобретение блага Y у индивида остается

126 – 4 ? 21 = 42 ден.ед. Тогда при Р_Y = 7 индивид купит 42/7 = 6 ед.

№ 6. Индивид имеет 6 ед. блага X и 8 ед. блага Y. Его функция полезности: 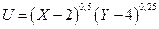. За какое минимальное количество блага X индивид согласится отдать 3 ед. блага Y?

Решение:

За такое количество, которое сохранит достигнутый уровень благосостояния, то есть:

U₀ = U₀ ’ → (6 -2) 0,5 (8- 4) 0,25 = (X₁ — 2) 0,5 (5 — 4) 0,25 → X₁ = 10. Следовательно, индивид согласится отдать 3 ед. блага Y за 4 ед. блага X.

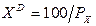
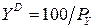
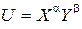
№ 7. Индивид предъявляет спрос на два блага, отображающийся функциями и . Определите общую полезность благ, купленных индивидом при Р_X =4 и Р_Y =1, если известно, что она измеряется функцией и a + b = 1.

Решение:

Чтобы определить общую полезность товарного набора следует найти X и Y, а также a и b. Для этого заданные цены благ подставляем в функции спроса и получаем: X = 100/4 = 25 ед; Y = 100/1 = 100 ед. Для определения абсолютного значения a и b используем условие оптимума покупателя: MU_X/MU_Y = P_X/P_Y , тогда:

При условии, что a + b = 1 и a = b получаем, что a = b = 0,5. Тогда по заданной функции полезности U = 25 0,5 × 100 0,5 = 5×10 = 50 ютил.

№ 8. Бюджет индивида равен 200 ден. ед. При цене блага Y Р_Y = 5 его линия «цена–потребление» отображается формулой Y=X+4

1. На сколько единиц индивид изменит потребление каждого блага при снижении цены блага X с 5 до 4 ден. ед?

2. Используя данные задачи постройте кривую спроса.

Решение:

Ассортимент потребляемых благ определяется точкой пересечения бюджетной линии с линией «цена–потребление» (точкой касания бюджетной линии с кривой безразличия).

Системы уравнений при P_X = 5 и P_X = 4 соответственно:

Тогда ΔX = 20-18 = 2 ед., ΔY = 24-22 = 2 ед.

Пункт 2 выполните самостоятельно.

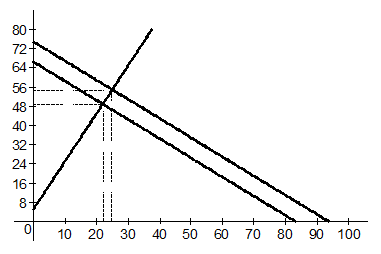
№ 9. При ценах Р_X = 4; Р_y = 5 линия «доход – потребление» индивида имеет вид: Y = 2X + 5.

1. На сколько единиц индивид увеличит потребление каждого блага при увеличении его бюджета с 333 до 375 ден. ед?

Решение:

Ассортимент потребляемых благ определяется точкой пересечения бюджетной линии с линией «доход–потребление» (точкой касания бюджетной линии с кривой безразличия).

Системы уравнений при бюджетах 333 и 375 ден.ед. соответственно:

Тогда потребление блага X изменится на 25-22 = 3 ед., блага Y изменится на 55-49 = 6 ед.

Рис. 1.2. Линия «доход-потребление»

Пункт 2 выполните самостоятельно.

№ 10. Функция полезности индивида имеет вид:

U = XY, его бюджет I = 56 , а цены благ P_X = 2, P_Y = 2.

1. Какое количество каждого из благ должен купить индивид для максимизации общей полезности?

2. Вывести уравнение кривой безразличия, на которой находится потребитель в момент равновесия.

3. Определить эффекты замены и дохода, если цена блага X повысилась до P_X = 8:

Будут ли одинаковыми эффекты замены и дохода по Хиксу и по Слуцкому? Как будут направлены эффекты замены и дохода при повышении цены на нормальное благо?

4. Определить разность между компенсирующим и эквивалентным изменениями дохода.

Решение:

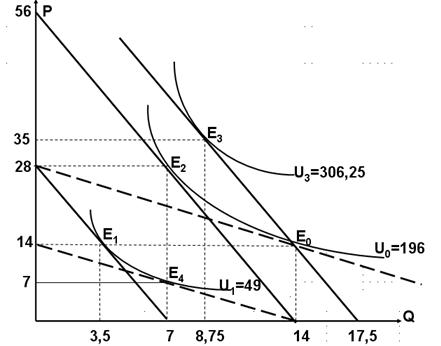
1. Оптимальную комбинацию благ (точка Е₀) ищем, решая систему уравнений:

2. В исходных условиях U₀ = 14 ? 14 = 196. Для любой точки данной функции справедливо: 196 = XY, следовательно, уравнение кривой безразличия будет иметь вид: .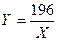

3. а) Повышение цены блага X изменит исходную систему уравнений, решение которой даст новые значения оптимума (точка Е₁):

Общий эффект изменения цены по Хиксу составит:

Общий эффект изменения цены по Хиксу разложим на эффект замены и эффект дохода, исходя из того, что по Хиксу при разложении общего эффекта сохраняется первоначальный уровень полезности. Для этого найдем координаты точки касания новой бюджетной линии (точнее касательной параллельной новой бюджетной линии) с первоначальной кривой безразличия, исходя из того, что в точке касания обе линии имеют одинаковый наклон (точка Е₂):

MRS_XY = .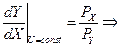

Следовательно, эффект замены:

а эффект дохода:

б) Общий эффект изменения цены по Слуцкому будет таким же как и по Хиксу. Разложим общий эффект изменения цены на эффект дохода и замены. По логике Слуцкого, после изменения цены товара потребитель должен иметь возможность купить тот же самый товарный набор. Следовательно, вспомогательная бюджетная линия должна пройти через точку с координатами (X₀; Y₀).

При новой цене блага Х он должен иметь в своем распоряжении 140 ден. ед., а не 56. Уравнение новой бюджетной линии имеет вид: 140 = 8X + 2Y. Эта линия станет касательной к некой кривой безразличия с более высоким уровнем полезности. Найдем координаты оптимума (точка Е₃):

X₃ = 8,75 и Y₃ = 35.

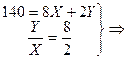
Следовательно, эффект замены:

а эффект дохода:

Если сравнить полученные результаты с результатами разложения по Хиксу, то из расчетов видно, что они численно не совпадают.

4. Для покупки исходной потребительской корзины при новой цене блага X (Р_Х=8) индивиду нужно иметь бюджет: I = (8×14 + 2×14) = 140 ден. ед., тогда компенсирующее изменение дохода (сумма денег для сохранения благосостояния индивида после повышения цены) составит: (140 – 56) = 84.

Для определения эквивалентного изменения дохода (максимальная сумма денег, которую потребитель готов заплатить за недопущение повышения цены до этого повышения) найдем координаты точки касания кривой безразличия U₁ с прямой, параллельной исходной бюджетной линии. Поскольку полезность в точке E₁, равна U₁ = 3,5×14 = 49, то для любой точки данной линии справедливо: 49 = XY. Тогда на основе уравнение кривой безразличия U₁ найдем координаты точки Е₄:

При исходных ценах такой набор благ можно купить при бюджете I=(2× 7 + 2×7)= 28 ден.ед.

Эквивалентное изменение дохода равно (56 – 28) = 28.

Разность между компенсирующим и эквивалентным изменениями дохода: 84 − 28 = 56.

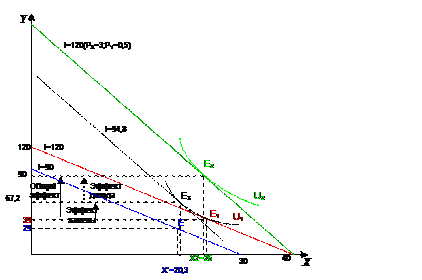
*№ 11. Известна функция полезности индивида 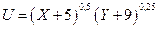, его бюджет I = 120 и цены благ P_X = 3; P_Y = 1.

1. Сколько единиц каждого блага купит индивид?

2. Сколько единиц каждого блага купит индивид в случае: а) уменьшении его бюджета до 90; б) снижения цены блага Y до P_Y = 0,5?

3. Сколько единиц каждого блага купит индивид в случае снижения цены блага Y до P_Y = 0,5 под воздействием эффекта замены (без учета эффекта дохода)?

4. Определите компенсирующее изменение бюджета потребителя в случае снижения цены блага Y до P_Y = 0,5.

5. Рассчитайте коэффициент перекрестной эластичности спроса на благо X при исходных значениях бюджета и цен и определите, являются товары X и Y для данного потребителя взаимозаменяемыми или взаимодополняемыми.

6. Рассчитайте коэффициент эластичности спроса на благо Y по бюджету при исходных значениях бюджета и цен.

Решение:

Нам необходимо найти координаты точки Е₃ ,которая лежит на U₁ и является касательной к вспомогательной бюджетной линии с углом наклона

Эффект замены:

5)Чтобы определить коэффициент перекрёстной эластичности спроса на благо X при исходных значениях бюджета и цен необходимо вывести функцию спроса на товар X — 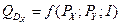, которую выводим из условия оптимума потребителя:

6) Чтобы рассчитать коэффициент эластичного спроса на благо Y по I , необходимо вывести функцию спроса на товар Y. Используя вычисленные значения из п.5,получаем:

Рис. 1.3 Эффекты дохода и замены.

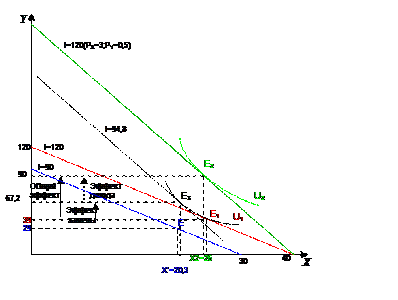
*№ 12. Индивид имеет функцию полезности U(X, Y) = X 0,75 ? Y 0,25 I = 100, Р_x = 4, Р_y = 2. Найти оптимум индивида и вывести функции его спроса на блага X и Y через функцию Лагранжа.

Решение:

1. Выражение Лагранжа:

L = x 0,75 ? y 0,25 + l (100 – 4 ? x – 2 ? y)

2. Дифференцируем выражение Лагранжа и приравниваем к нулю, полученные производные:

(*)

(**)

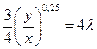
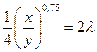
3. Решение системы уравнений.

Уравнение (*) делим на уравнение (**) и получаем: =>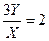

Полученное значение X подставляем в уравнение (***), тогда: ; .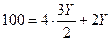

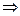
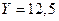
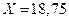
4. Выведение функций спроса на благо.

При степенной функции полезности функция спроса на благо для потребителя может быть получена на основе выражения Лагранжа:

−

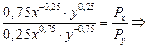
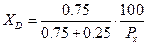
функция спроса на благо X, тогда функция спроса на благо Y будет иметь вид:

.

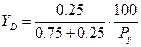
Источник