Выведите расчетную формулу для определения показателя адиабаты

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ

Цель работы: познакомиться с адиабатическим процессом, определить показатель адиабаты для воздуха.

Оборудование: баллон с клапаном, компрессор, манометр.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

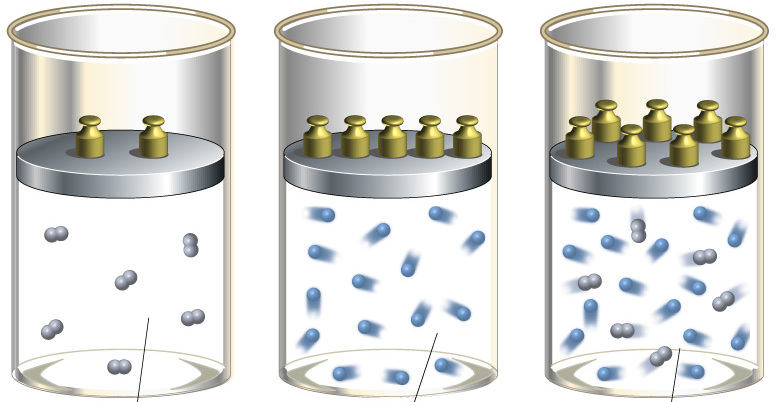
Адиабатический процесс – это процесс, протекающий в термодинамической системе без теплообмена с окружающей средой. Термодинамической системой является система, содержащая огромное количество частиц. Например, газ, число молекул которого сравнимо с числом Авагадро 6,02∙10 23 1/моль. Хотя движение каждой частицы подчиняется законам Ньютона, но их так много, что решить систему уравнения динамики для определения параметров системы невозможно. Поэтому состояние системы характеризуют термодинамическими параметрами, такими как давление P, объем V, температура T.

Согласно первому началу термодинамики, являющемуся законом сохранения энергии в термодинамических процессах, теплота Q, подводимая к системе, расходуется на совершение работы А и на изменение внутренней энергии Δ U

Теплота – это количество энергии хаотического движения, передаваемое термодинамической системе. Подвод теплоты приводит к повышению температуры: , где n – количество газа, С − молярная теплоемкость, зависящая от вида процесса. Внутренняя энергия идеального газа − это кинетическая энергия молекул. Она пропорциональна температуре: , где C_v – молярная теплоемкость при изохорическом нагревании. Работа элементарного изменения объема силами давления равна произведению давления на изменение объема: dA= PdV.

Для адиабатического процесса, происходящего без теплообмена (Q = 0), работа совершается за счет изменения внутренней энергии, A = − D U. При адиабатическом расширении работа газа положительна, поэтому внутренняя энергия и температура понижаются. При сжатии – наоборот. Все быстро протекающие процессы можно достаточно точно считать адиабатическими.

Выведем уравнениеадиабатического процесса идеального газа. Для этого применим уравнение первого начала термодинамики для элементарного адиабатического процесса dA= − dU, котороепринимает вид РdV =−n С_vdT . Добавим к этому дифференциальному уравнению еще одно, полученное дифференцированием уравнения Менделеева–Клапейрона (PV=νRT): PdV +VdP =nR dT. Исключая в двух уравнениях один из параметров, например, температуру, получим соотношение для двух других параметров . Интегрируя и потенцируя, получим уравнение адиабаты через давление и объем:

T V g -1 = const, P g -1 T — g = const. (2)

Здесь 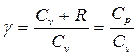– показатель адиабаты, равный отношению теплоемкостей газа при изобарическом и изохорическом нагревании.

Получим формулу для показателя адиабаты в молекулярно-кинетической теории. Молярная теплоемкость по определению это количество теплоты, необходимое для нагревания одного моля вещества на один Кельвин . При изохорическом нагревании теплота расходуется только на повышение внутренней энергии . Подставив теплоту, получим .

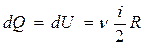
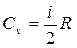
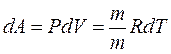
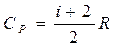
Приизобарическом нагревании газа в условиях постоянного давления дополнительно часть теплоты расходуется на работу изменения объема . Поэтому количество теплоты, (dQ = dU + dA) полученное при изобарическом нагревании на один Кельвин будет равно . Подставив в формулу теплоемкости, получим .

Тогда показатель адиабаты может быть определен теоретически по формуле

. (3)

Здесь i – число степеней свободы молекул газа. Это число координат, достаточное для определения положения молекулы в пространстве или число составляющих компонентов энергии молекулы. Например, для одноатомной молекулы кинетическая энергия может быть представлена как сумма трех компонентов энергии, соответствующих движению вдоль трех осей координат, i = 3. Для жесткой двухатомной молекулы следует добавить еще два компонента энергии вращательного движения, так как энергия вращения относительно третьей оси, проходящей через атомы, отсутствует. Итак, для двухатомных молекул i = 5. Для воздуха как для двухатомного газа теоретическое значение показателя адиабаты будет равно g = 1,4.

Показатель адиабаты можно определить экспериментально методом Клемана – Дезорма. В баллон нагнетают воздух, сжимая до некоторого давления Р₁ , немного больше атмосферного. При сжатии воздух несколько нагревается. После установления теплового равновесия баллон на короткое время открывают. В этом процессе расширения 1–2 давление падает до атмосферного Р₂=Р_атм, а исследуемая масса газа, которая до этого занимала часть объема баллона V₁, расширяется, занимая весь баллон V₂ (рис.1). Процесс расширения воздуха (1−2) происходит быстро, его можно считать адиабатическим, происходящим по уравнению (2)

. ( 4)

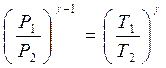
В адиабатическом процессе расширения воздух охлаждается. После закрытия клапана охлажденный воздух в баллоне через стенки баллона нагревается до температуры лаборатории Т ₃= Т₁. Это изохорический процесс 2–3

. (5)

Решая совместно уравнения (4) и (5), исключая температуры, получим уравнение, , из которого следует определить показатель адиабаты γ. Датчик давления измеряет не абсолютное давление, которое записано в уравнениях процессов, а избыточное над атмосферным давлением. То есть Р₁ = ΔР₁+ Р₂, и Р₃ =ΔР₃+Р₂. Переходя к избыточным давлениям, получим . Избыточные давления невелики по сравнению с атмосферным давлением Р₂ . Разложим члены уравнения в ряд по соотношению . После сокращения на Р₂ получим для показателя адиабаты расчетную формулу

. (6)

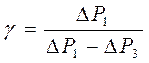
Лабораторнаяустановка (рис. 2) состоит из стеклянного баллона, который сообщается с атмосферой через клапан Атмосфера. Воздух накачивается в баллон компрессором при открытом кране К. После накачивания, во избежание утечки воздуха, кран закрывают.

1. Включить установку в сеть 220 В.

Открыть кран баллона. Включить компрессор, накачать воздух до избыточного давления в диапазоне 4 –11 кПа. Закрыть кран баллона. Выждать 1,5 –2 мин, записать величину давления ΔР₁ в таблицу.

2. Повернуть клапан Атмосфера до щелчка, клапан откроется и захлопнется. Произойдет адиабатический сброс воздуха с понижением температуры. Следить за повышением давления в баллоне по мере нагрева. Измерить наивысшее давление ΔР₃ после установления теплового равновесия. Результат записать в таблицу.

Повторить опыт не менее пяти раз, изменяя исходное давление в диапазоне 4–11 кПа.

ΔР1, кПа

ΔР3, кПа

γ

3. Произвести расчеты. Определить показатель адиабаты в каждом опыте по формуле (6). Записать в таблицу. Определить среднее значение показателя адиабаты

4. Оценить случайную погрешность измерения по формуле для прямых измерений

. (7)

5. Записать результат в виде g = ± dg. Р = 0,9. Сравнить результат с теоретическим значением показателя адиабаты двухатомного газа g _теор = 1,4.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение адиабатического процесса. Запишите первое начало термодинамики для адиабатического процесса. Объясните изменение температуры газа при адиабатических процессах сжатия и расширения.

2. Выведите уравнение адиабатического процесса для параметров давление – объем.

3. Выведите уравнение адиабатического процесса для параметров давление – температура.

4. Дайте определение числа степеней свободы молекул. Как зависит внутренняя энергия идеального газа от вида молекул?

5. Как осуществляются процессы с воздухом в цикле Клемана – Дезорма, как изменяются давления и температуры в процессах?

6. Выведите расчетную формулу для экспериментального определения показателя адиабаты.

Источник

Показатели адиабаты: определение и процесс

При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.

Адиабатический процесс

Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:

• теплопроводность между внешней средой и системой по той или иной причине является низкой;
• скорость процесса велика, поэтому обмен теплом не успевает происходить.

В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.

Уравнение Пуассона для адиабаты идеального газа

Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.

Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:

Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.

В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:

Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.

Что такое показатель адиабаты?

Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом C_P изобарную теплоемкость, а символом C_V — изохорную. Тогда для γ справедливо равенство:

Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.

Теплоемкости CP и CV

Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин C_P и C_V. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:

Величина C_V определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.

Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:

Отсюда видно, что C_P>C_V, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.

Величина γ для газа идеального одноатомного

Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:

Откуда можно определить значение изохорной теплоемкости C_V:

Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:

Из последних двух равенств следует значение показателя адиабаты:

Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.

Зависимость γ от числа степеней свободы

Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.

Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для C_V приобретает вид:

Тогда значение γ будет равно:

Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.

Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:

Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.

Показатель адиабаты для смеси газов

Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна a_i. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:

Где γ_i — это величина γ для i-го компонента.

Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.

Источник