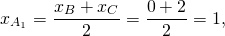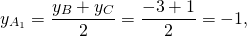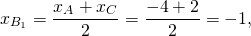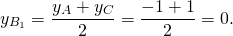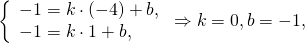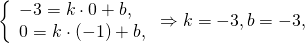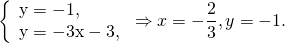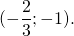Выведите формулы выражающие координаты точки пересечения медиан треугольника через координаты его

Выведите формулы, выражающие координаты точки пересечения медиан треугольника через координаты его вершин

уравнение прямой, проходящей через 2 заданные точки:
(y-y1)/(y2-y1)=(x-x1)/(x2-x1)
уравнение медианы — это (x1,y1) — координата третьей вершины (например, С) ,
x2=(xA+xB)/2, y2=(yA+yB)/2
то же самое делаем с другой медианой (все три пересекутся в одной точке, поэтому неважно, какую выбрать)
чтобы две прямые пересеклись — надо решить систему уравнений:

A(x1;y1), B(x2;y2), C(x3;y3)
AM, BN — медианы треугольника, O — точка пересечения медиан.
Так как M — середина BC, то ее координаты:
M((x2+x3)/2;(y2+y3)/2)
Находим координаты вектора AM
AM = ((x2+x3)/2-x1;(y2+y3)/2-y1)
AM = ((x2+x3-2×1)/2;(y2+y3-2y1)/2)
Дальше используем свойство, что медианы точкой пересечения делятся в отношении 2 к 1, считая от вершины, то есть AO = 2 * OM,
Тогда
AO = 2/3 * AM
Значит вектора AO
AO = (2/3 * (x2+x3-2×1)/2;2/3 * (y2+y3-2y1)/2)
AO = ((x2+x3-2×1)/3;(y2+y3-2y1)/3)
Осталось найти координаты точки O(x0;y0)
AO = (x0 — x1; y0 — y1)
Значит

x0 — x1 = (x2 + x3 — 2 * x1)/3 => x0 = (x1 + x2 + x3)/3

y0 — y1 = (y2 + y3 — 2 * y1)/3 => y0 = (y1 + y2 + y3)/3

уравнение прямой, проходящей через 2 заданные точки:
(y-y1)/(y2-y1)=(x-x1)/(x2-x1)
уравнение медианы — это (x1,y1) — координата третьей вершины (например, С) ,
x2=(xA+xB)/2, y2=(yA+yB)/2
то же самое делаем с другой медианой (все три пересекутся в одной точке, поэтому неважно, какую выбрать)
чтобы две прямые пересеклись — надо решить систему уравнений:

или такПусть координаты таковы:
A(x1;y1), B(x2;y2), C(x3;y3)
AM, BN — медианы треугольника, O — точка пересечения медиан.
Так как M — середина BC, то ее координаты:
M((x2+x3)/2;(y2+y3)/2)
Находим координаты вектора AM
AM = ((x2+x3)/2-x1;(y2+y3)/2-y1)
AM = ((x2+x3-2×1)/2;(y2+y3-2y1)/2)
Дальше используем свойство, что медианы точкой пересечения делятся в отношении 2 к 1, считая от вершины, то есть AO = 2 * OM,
Тогда
AO = 2/3 * AM
Значит вектора AO
AO = (2/3 * (x2+x3-2×1)/2;2/3 * (y2+y3-2y1)/2)
AO = ((x2+x3-2×1)/3;(y2+y3-2y1)/3)
Осталось найти координаты точки O(x0;y0)
AO = (x0 — x1; y0 — y1)
Значит
x0 — x1 = (x2 + x3 — 2 * x1)/3 => x0 = (x1 + x2 + x3)/3
y0 — y1 = (y2 + y3 — 2 * y1)/3 => y0 = (y1 + y2 + y3)/3A(x1;y1), B(x2;y2), C(x3;y3)
AM, BN — медианы треугольника, O — точка пересечения медиан.
Так как M — середина BC, то ее координаты:
M((x2+x3)/2;(y2+y3)/2)
Находим координаты вектора AM
AM = ((x2+x3)/2-x1;(y2+y3)/2-y1)
AM = ((x2+x3-2×1)/2;(y2+y3-2y1)/2)
Дальше используем свойство, что медианы точкой пересечения делятся в отношении 2 к 1, считая от вершины, то есть AO = 2 * OM,
Тогда
AO = 2/3 * AM
Значит вектора AO
AO = (2/3 * (x2+x3-2×1)/2;2/3 * (y2+y3-2y1)/2)
AO = ((x2+x3-2×1)/3;(y2+y3-2y1)/3)
Осталось найти координаты точки O(x0;y0)
AO = (x0 — x1; y0 — y1)
Значит

x0 — x1 = (x2 + x3 — 2 * x1)/3 => x0 = (x1 + x2 + x3)/3

y0 — y1 = (y2 + y3 — 2 * y1)/3 => y0 = (y1 + y2 + y3)/3

уравнение прямой, проходящей через 2 заданные точки:
(y-y1)/(y2-y1)=(x-x1)/(x2-x1)
уравнение медианы — это (x1,y1) — координата третьей вершины (например, С) ,
x2=(xA+xB)/2, y2=(yA+yB)/2
то же самое делаем с другой медианой (все три пересекутся в одной точке, поэтому неважно, какую выбрать)
чтобы две прямые пересеклись — надо решить систему уравнений:

Источник

Выведите формулы выражающие координаты точки пересечения медиан треугольника через координаты его вершин

Вопрос по геометрии:

Выведите формулы выражающие координаты точки пересечения медиан треугольника через координаты его вершин

Ответы и объяснения 1

Пусть координаты таковы:
A(x1;y1), B(x2;y2), C(x3;y3)
AM, BN — медианы треугольника, O — точка пересечения медиан.
Так как M — середина BC, то ее координаты:
M((x2+x3)/2;(y2+y3)/2)
Находим координаты вектора AM
AM = ((x2+x3)/2-x1;(y2+y3)/2-y1)
AM = ((x2+x3-2×1)/2;(y2+y3-2y1)/2)
Дальше используем свойство, что медианы точкой пересечения делятся в отношении 2 к 1, считая от вершины, то есть AO = 2 * OM,
Тогда
AO = 2/3 * AM
Значит вектора AO
AO = (2/3 * (x2+x3-2×1)/2;2/3 * (y2+y3-2y1)/2)
AO = ((x2+x3-2×1)/3;(y2+y3-2y1)/3)
Осталось найти координаты точки O(x0;y0)
AO = (x0 — x1; y0 — y1)
Значит
x0 — x1 = (x2 + x3 — 2 * x1)/3 => x0 = (x1 + x2 + x3)/3
y0 — y1 = (y2 + y3 — 2 * y1)/3 => y0 = (y1 + y2 + y3)/3

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

Выведите формулы выражающие координаты точки пересечения медиан треугольника через координаты его вершин?

Геометрия | 10 — 11 классы

Выведите формулы выражающие координаты точки пересечения медиан треугольника через координаты его вершин.

Пусть координаты таковы :

A(x1 ; y1), B(x2 ; y2), C(x3 ; y3)

AM, BN — медианы треугольника, O — точка пересечения медиан.

Так как M — середина BC, то ее координаты :

M((x2 + x3) / 2 ; (y2 + y3) / 2)

Находим координаты вектора AM

AM = ((x2 + x3) / 2 — x1 ; (y2 + y3) / 2 — y1)

AM = ((x2 + x3 — 2×1) / 2 ; (y2 + y3 — 2y1) / 2)

Дальше используем свойство, что медианы точкой пересечения делятся в отношении 2 к 1, считая от вершины, то есть AO = 2 * OM,

Значит вектора AO

AO = (2 / 3 * (x2 + x3 — 2×1) / 2 ; 2 / 3 * (y2 + y3 — 2y1) / 2)

AO = ((x2 + x3 — 2×1) / 3 ; (y2 + y3 — 2y1) / 3)

Осталось найти координаты точки O(x0 ; y0)

AO = (x0 — x1 ; y0 — y1)

x0 — x1 = (x2 + x3 — 2 * x1) / 3 = &gt ; x0 = (x1 + x2 + x3) / 3

y0 — y1 = (y2 + y3 — 2 * y1) / 3 = &gt ; y0 = (y1 + y2 + y3) / 3.

В треугольнике ABC точка O является точкой пересечения его медиан?

В треугольнике ABC точка O является точкой пересечения его медиан.

В треугольнике AOC проведена медиана ON.

Найдите координаты вектора BN, если ON< - 3 ; - 1>.

Выведите формулы координат середины отрезка по координатам его концов?

Выведите формулы координат середины отрезка по координатам его концов.

Треугольник задан координата вершин?

Треугольник задан координата вершин.

Как найти высоту.

Мне формулу только.

Треугольник ОАВ проведенна медиана ОМ?

Треугольник ОАВ проведенна медиана ОМ.

Определите координаты точки М и ее длину, если точки А и В имеют координаты А( — 5, 0), В(0, 3), а точка О является началом координат.

Вершины треугольника АВС имеют координаты : A( — 2 ; 2), В(1 ; 4), С(0 ; 0>?

Вершины треугольника АВС имеют координаты : A( — 2 ; 2), В(1 ; 4), С(0 ; 0>.

Составьте уравнения сторон и медиан этого треугольника.

Гlри составлении уравнений медиан треугольника предварительно найдите координаты середин его стоион.

Выведите формулу для вычисления расстояния между точками с заданными координатами?

Выведите формулу для вычисления расстояния между точками с заданными координатами.

1) В треугольнике ABC MN — средняя линия, M принадлежит AB, N принадлежит BC, О — точка пересечения медиан?

1) В треугольнике ABC MN — средняя линия, M принадлежит AB, N принадлежит BC, О — точка пересечения медиан.

Найти координаты вершин треугольника, если известны координаты точек О (1 ; — 2), М (2 ; — 1) и N(0 ; — 1) 2) Найдити длины медиан AN и СM.

Вершины треугольника АВС имеют координаты А( — 2 ; 0 ; 1) В( — 1 ; 2 ; 3)С(8 ; — 4 ; 9)Найдите координаты вектора ВМ, если ВМ — медиана треугольника?

Вершины треугольника АВС имеют координаты А( — 2 ; 0 ; 1) В( — 1 ; 2 ; 3)С(8 ; — 4 ; 9)Найдите координаты вектора ВМ, если ВМ — медиана треугольника.

Найдите длину медианы ВМ, треугольника АВС, если координаты вершин треугольника А(2 ; 5), В(0 ; 0), С(4 ; 3)?

Найдите длину медианы ВМ, треугольника АВС, если координаты вершин треугольника А(2 ; 5), В(0 ; 0), С(4 ; 3).

Треугольник АВС задан координатами своих вершин а( — 5 4 2) в (2 3 1) с ( — 3 — 1 — 3) найти : a) периметр треугольника АВС б) косинус угла между сторонами АВ и ВС в)длину медианы ВМ г)длину средней л?

Треугольник АВС задан координатами своих вершин а( — 5 4 2) в (2 3 1) с ( — 3 — 1 — 3) найти : a) периметр треугольника АВС б) косинус угла между сторонами АВ и ВС в)длину медианы ВМ г)длину средней линии НМ║ ВС д) координаты точки пересечения медиан е) считая, что точка А, В, С — три вершины параллелограмма, найти координаты четвёртой вершины.

На этой странице находится вопрос Выведите формулы выражающие координаты точки пересечения медиан треугольника через координаты его вершин?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

Нам известно 2 угла в прямоугольном треугольнике. Найдем последний : 90 — 45 = 45. Получается равнобедренный треугольник NK = MN = 4см. (при условии что MN — катет). Если гипотенуза, то аналогично находим оставшийся катет и по т. Пифагора гипоте..

DOB — прямоугольный т. Е равен 90° 90 — 42 = 48° Ответ : 48°.

1. один угол х, другой х + 26 сумма углов равна 360 2(х + (х + 26)) = 360 4х + 52 = 360 4х = 308 х = 77 значит второй угол равен х + 26 = 103.

Точки могут быть расположены так : — — — А — — — — — — — — — — В — — — — — — — — — С — — — ВС = АС — АВ = 35 — 27 = 8 или так : — — — В — — — — — — — — — — — А — — — — — — — — — С — — — ВС = АВ + АС = 27 + 35 = 62.

Если A. B. C. D — расположены в порядке возрастания, то A = 0, 13. B = 0, 3. C = 1, 03. D = 1, 12.

Высота СД делит треугольник АВС на два подобных треугольника. СД² = АД·ВД = 5·15 = 75. СД = 5√3 см. В тр — ке АСД АС² = СД² + АД² = 75 + 5² = 100, АС = 10 см — меньший катет. Коэффициент подобия тр — ков АСД и ВСД : k = СД / ВД = 5√3 / 15 = √3 / ..

Первая 3 в скобках означает Х , а вторая — у Подставляем в функцию : 3 = 3 * 3 — 6 3 = 9 — 6 3 = 3 График функции проходит через точку A (3 ; 3) Вот если бы была точка , например, Б ( — 3 ; 5) 5 = — 3 * 3 — 6 5 = — 15 5 не = — 15, значит, график не п..

А) 6. 5 см б) B — 30 гр. C — 60 гр. В) угол М — 67 гр.

Если все ребра пирамиды равны, – равны и их проекции, и основание высоты пирамиды совпадает с центром описанной окружности. АС = 3, угол СВА = 30° По т. Синусов 2R = AC : sin30°, R = (3 : 0, 5) : 2 = 3 Из прямоугольного треугольника АОМ высота пира..

Источник

Точка пересечения медиан треугольника

Как найти точку пересечения медиан треугольника, зная координаты его вершин?

Поскольку все медианы треугольника пересекаются в одной точке, достаточно составить уравнения двух медиан и найти координаты их точки пересечения.

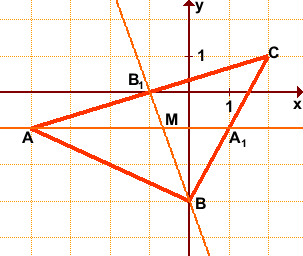
Найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1).

Обозначим середины сторон BC и AC через A₁ и B₁ соответственно. По формулам координат середины отрезка

Составим уравнения медиан AA₁ и BB₁.

Уравнение медианы AA₁ можно найти как уравнение прямой, проходящей через две точки A(-4;-1) и A₁(1;-1).

то есть уравнение прямой AA₁ y= -1.

B(0;-3), B₁(-1;0). Найдём уравнение медианы BB₁.

откуда уравнение прямой BB₁ y= -3x-3.

Координаты точки пересечения прямых AA₁ и BB₁ ищем как решение системы уравнений

Поскольку все медианы медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины, можно найти координаты концов любой медианы, а затем точку, которая делит медиану в отношении 2:1, начиная отсчёт от точки, которая является вершиной треугольника.

Например, в условиях предыдущей задачи — найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1), —

зная координаты A₁(1;-1), найдём координаты точки M. Точка M пересечения медиан треугольника делит отрезок AA₁ в отношении 2:1, считая от точки A.

Источник