Выведите формулу площади треугольника содержащую синус угла

Площадь треугольника через синус

Определение

Площадь треугольника через синус — это площадь треугольника,
выраженная через две любые стороны треугольника и синус угла между ними.

Синус угла — это число, которое используется для нахождения
разных величин в треугольниках, его можно найти в специальных таблицах.

Введение

Площадь треугольника кроме половины произведения высоты
на основания, можно также найти и другим способом.
Мало кто знает, но через синусы углов можно найти обычно
не только стороны, но и площадь любого треугольника!

Площадь треугольника выраженная без синуса численно равна
половине произведения двух сторон друг на друга
на синус угла между ними.

Площадь треугольника через синус ищется только в том случае,
если по другой формуле площадь треугольника найти нельзя.

Теорема

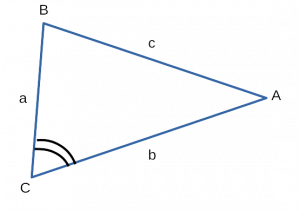
\( S = \frac<1>2 * BC * AC * \sin \angle BCA \) ​

Площадь произвольного треугольника равна полусумме
произведения двух любых сторон треугольника друг на друга,
и на синус угла между этими сторонами.

Формула

\[ S = \frac<1>2 * a * b * \sin α \]

Где a, b — две стороны треугольника, синус α — синус угла α.

Пример

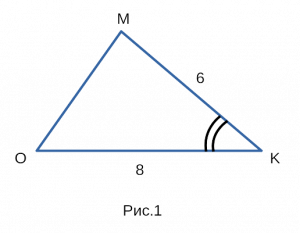
Для примера, возьмем треугольник omk, изображенный на рисунке 1, со сторонами om, mk, ok.
Известно, что mk равен 6, ok равен 8, синус угла okm равен 1/4.

Нужно найти площадь треугольника omk.

Дано: △omk, mk = 6, ok = 8, sin okm = 1/4.

Найти: S △omk — ?

Решение:

1) ​ \( S = \frac<1>2*a*b*\sin α \) ​​ \( \implies \) ​ \( S = \frac<1>2*mk*ok*\sin okm \) ​

2) S = 1/2 * 6 * 8 * 1/4 = 1/2 * 6 * 8 * 0.25 = 1/2 * 48 * 0.25 = 1/2 * 12 = 6

Ответ: Площадь треугольника omk равна 6.

Доказательство

Докажем, что площадь произвольного треугольника
равна полусумме произведения двух любых сторон
друг на друга, и на синус угла между этими сторонами.

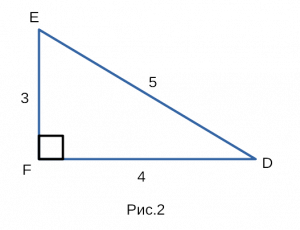
Чтобы вам наглядно было видно, как мы доказываем,
используем один из известнейших треугольников — египетский треугольник.
Высота в египетском треугольнике равна длине одного из катетов.
Построим прямоугольный треугольник, изображенный на рисунке 2,
со сторонами 3,4,5 с одним из углов 90 градусов.

Первым делом найдем площадь обычной формулой,
затем с помощью синуса. Площадь равна половине
основания на высоту — ½3*4 = 6. Теперь найдем с
помощью синуса: ½3*4*sin90 = 6 * 1 = 6. Как видим,
полученные значения площадей сходятся, соответственно
через синус можно найти площадь треугольника ч.т.д.

Теперь, чтобы найти площадь треугольника нам не нужно
знать основание и высоту, можно знать только
две стороны и синус угла между ними.

Заключение

В заключение, можно сказать, что площадь
треугольника можно найти разными способами.
Например, в прямоугольном треугольнике площадь
рассчитать легче чем в любом другом треугольнике,
так как высота уже известна. Именно поэтому,
в школьном курсе, отчасти так подробно изучаются
прямоугольные треугольники. В Древнем Египте были
распространены прямоугольные треугольники со
сторонами 3,4,5; 6,8,10; 5,12,13. Длины этих прямоугольных
треугольников треугольников целые, что значительно,
упрощало разного рода вычисления.

Формулу площади треугольника делает универсальной то,
что она может применена к абсолютно любым треугольникам.
Главное, чтобы были известные две стороны,
и угол или синус угла между ними.

Формула площади треугольника через синус — универсальна,
поэтому может быть применена к любым видам треугольников.

Источник

Выведите формулу площади треугольника содержащую синус угла

Сформулируем, проанализируем и докажем теорему о площади треугольника.

Теорема звучит так:

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Запишем данную теорему в стандартных для треугольника обозначениях.

Рис. 1. Площадь треугольника

Формула площади треугольника (рис. 1) имеет такой вид:

Докажем данную теорему.

Дано: (рис. 2)

Доказать:

Доказательство:

Любой треугольник АВС имеет не менее двух острых углов, так как сумма углов треугольника равна 180 градусов. Пусть острыми являются угол и угол . Тогда высота АН= находится внутри треугольника АВС, потому что иначе сумма углов в треугольнике (рис. 2) превышала бы 180 градусов (угол прямой, так как – высота; а угол при вершине В тупой, так как угол (по условию).

Рис. 2. Иллюстрация к теореме

Получили два прямоугольных треугольника общим катетом АН=. Для нахождения данного катета мы используем свойство сторон и углов прямоугольного треугольника: гипотенузу умножаем на синус противолежащего угла:

Подставим данное значение в формулу площади треугольника:

Мы доказали две формулы из трёх через острые углы . Если угол α острый, доказательство будет аналогичное. Если угол α будет прямым, доказательство очевидное (. При высота С= находится вне треугольника АВС (рис. 3).

Рис. 3. Иллюстрация к теореме

Рассмотрим треугольник . В нём угол . Чтобы найти катет , нужно гипотенузу умножить на синус противолежащего угла:

Подставляем в формулу для площади треугольника () значение катета :

Мы доказали и третью формулу. Следовательно, доказали теорему.

Также эту теорему можно доказать координатным методом (рис. 4).

Дано: треугольник АВС, ,

Доказать:

Рис. 4. Иллюстрация к теореме

Координаты вершины А определяются через длину АС=b и угол γ. В предыдущих уроках мы выяснили, что координаты точки А будут . А – это высота , то есть ордината точки А.

Подставляем в формулу площади треугольника:

Формула доказана независимо от величины углов треугольника – за начало координат была взята точка С. Остальные 2 формулы получаются аналогично, если за начало координат взять точку А или В.

Полученные формулы можно использовать во многих задачах.

Дано: треугольник АВС, АВ= см, АС=4 см, ⦟А=(рис. 5)

Найти: площадь треугольника АВС

Решение:

Рис. 5. Иллюстрация к задаче

Для решения данной задачи воспользуемся ранее доказанной теоремой.

Подставляем известные значения:

Докажите, что площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Доказательство:

Для доказательства воспользуемся свойствами параллелограмма. Диагональ BD рассекает параллелограмм на два треугольника. (рис. 6) по трём равным сторонам (противоположные стороны в параллелограмме равны, следовательно, АВ=CD, AD=BC. Сторона BD – общая для двух треугольников.). Отсюда следует, что площади этих двух треугольников тоже равны.

Согласно теореме о площади треугольника

Рис. 6. Иллюстрация к задаче

Значит, площадь параллелограмма равна

=

Можно рассмотреть и угол В. Он равен , следовательно, . Поэтому площадь параллелограмма можно рассчитать через :

Формула для площади параллелограмма доказана.

Треугольники ADB и ADC параллелограмма ABCD . Доказать, что площади этих треугольников равны.

Доказательство:

Рис. 7. Иллюстрация к задаче

Площади первого и второго треугольника есть произведение половины основания на высоту (рис. 7). Основание у них одинаковое (AD), высота, опущенное на это основание, также одинаковая, следовательно:

Дано:, АС15 см,

Найти: сторону АВ (рис. 8)

Решение:

Рис. 8. Иллюстрация к задаче

Найдём сторону АВ через формулу площади треугольника

Подставляем известные величины:

см

Докажите, что площадь параллелограмма равна половине произведения длин его диагоналей на синус угла между ними.

Дано: ABCD – параллелограмм (рис. 9)

Доказать:

Доказательство: первый способ:

Учтём, что угол α и угол имеют один и тот же синус:

Площадь треугольника АОВ (согласно теореме о площади треугольника):

Площадь треугольника ВОС:

Рис. 9. Иллюстрация к задаче

Так как синусы равны, то и . Учитывая, что , а , мы доказали, что диагонали параллелограмма делят его на 4 равновеликих треугольника.

Поэтому для нахождения площади параллелограмма достаточно найти площадь одного из треугольников и умножить на 4.

Так как , то

Что и требовалось доказать.

Рис. 10. Иллюстрация к задаче

Из точки С диагонали АС проводим прямую CР, параллельную другой диагонали (BD). Получаем параллелограмм BDPC, треугольник ABD равновелик треугольнику DCP, так как

Основания и высота у них одинаковы.

Таким образом, отнимая от параллелограмма ABCD треугольник ABD и прибавляя треугольник DCP, получаем треугольник АСР с такой же площадью, как у исходного параллелограмма. И площадь этого треугольника равна:

Так как СРBD и , то

Что и требовалось доказать.

Дано: , , высота ВН=h

Найти: площадь треугольника АВС (рис. 11)

Решение:

Рис. 11. Иллюстрация к задаче

Согласно теореме о площади треугольника

Выражаем АВ и ВС через h и другие известные величины. АВ является

гипотенузой в прямоугольном треугольнике АВН, поэтому:

, при (рис. 11 а)

, при (рис. 11 б)

Аналогично находим ВС (). В обоих случаях:

Подставляем данные значения в формулу площади треугольника:

На данном уроке мы доказали теорему о площади треугольника через синус его

угла и решили задачи по данной теме.

Список литературы

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

1. В треугольнике ABC AB = 1 см, BC = 2 см, , . Найдите площадь треугольника.
2. Для определения площади треугольника АВС измерили две его стороны a и b и угол между ними γ. Вычислить площадь (a= 125 мм, b= 160 мм, γ = 52).
3. Площадь треугольника АВС равна 18. АС = ВС = 3. Найдите сторону АВ.

Источник