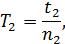ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ ОБОРОТНЫМ МАЯТНИКОМ
Цель работы: определить приведенную длину оборотного маятника и вычислить ускорение свободного падения.
Оборудование: оборотный маятник, секундомер.
Краткие теоретические сведения
Большинство косвенных методов измерения ускорения свободного падения 
основано на использовании формулы для периода гармонических колебаний физического маятника
Здесь J – момент инерции маятника относительно оси качания (точки подвеса), m – масса маятника, а – расстояние от оси качания до центра масс.
Величина 
называется приведенной длиной физического маятника. Тогда
Формула (1) для вычисления обычно не используются, так как измерение а и J представляет большие трудности. Применение оборотного маятника, который является частным случаем физического маятника, позволяет обойти эти трудности, потому что предлагаемый метод дает возможность определить без измерения момента инерции J и расстояния а.
Оборотный маятник (рис. 1) состоит из стержня, на котором закреплены опорные призмы П1 и П2. Между опорными призмами закреплен груз А. Второй груз В можно перемещать по стержню и закреплять в любом месте между призмойП2 и концом стержня.
Особенностью оборотного маятника является то, что в нем можно найти две такие точки, лежащие по разные стороны от центра масс С, что при последовательном подвешивании маятника за ту или другую точку период колебаний его остается одним и тем же.
Можно показать, что расстояние между этими точками равно приведенной длине маятника L.
Преобразуем формулу (1). Подставим в нее по теореме Штейнера выражение
где J0 – момент инерции маятника относительно оси, проходящей через центр масс С параллельно оси качаний, а величины J, m, a те же, что в формуле (1).
Если маятник совершает колебания на призме П1, то период колебания
Если маятник перевернуть и заставить качаться на призме П2, то период колебания
При перемещении грузов изменяется положение центра масс С (см. рис. 1) и, следовательно, изменяются величины а1 и а2. Можно добиться такого положения грузов на стержне, при котором T1 = T2 = T в пределах точности эксперимента.
Тогда (5) имеет вид
Докажем, что расстояние l = a1 + a2 между опорными призмами оборотного маятника при T1 = T2 = T равно приведенной длине L. Из (6) имеем
Сравнив формулы (2) и (7), видим, что, L = a1 + a2. Расчетная формула для ускорения свободного падения имеет вид
Сущность работы состоит в том, чтобы найти такое положение грузов на стержне, при котором периоды колебаний на призмах П1 и П2 были равны. Тогда, измерив величину периода T и приведенную длину оборотного маятника L = a1 + a2, по формуле (8) можно найти .
Описание установки и метода измерений
В основании1 (рис. 1) закреплена колонка2, на ней зафиксирован верхний кронштейн 3 и нижний кронштейн 4 с фотоэлектрическим датчиком 5. Нижний кронштейн можно перемещать вдоль колонки и фиксировать в любом положении.
Оборотный маятник выполнен в виде стальногостержня 6, на котором находятся две призмы 7 и два груза 8. На стержне через 1 см нанесены деления для определения приведенной длины маятника. Призмы и грузы можно перемещать вдоль стержня и фиксировать в любом положении. Время колебаний и число колебаний отображается на экране электронного секундомера 9.
Порядок выполнения работы
1. Закрепить один груз вблизи конца, а другой – вблизи середины стержня.
2. Закрепить призмы так, чтобы они были обращены друг к другу. Одну из них поместить вблизи свободного конца стержня, а другую – примерно на половине расстояния между грузами. Проверить, совпадают ли основания призм с делениями на стержне.
3. Закрепить маятник на вкладыше верхнего кронштейна на призме П1, находящейся вблизи конца стержня.
4. Нижний кронштейн вместе с фотодатчиком установить так, чтобы стержень маятника пересекал световой поток фотодатчика.
5. Отклонить маятник на 4º-5º от положения равновесия и отпустить.
6. Нажать клавишу «СБРОС» секундомера 9, при этом начинается отсчет времени t и числа полных колебаний n.
7. После подсчета измерителем n полных колебаний нажать клавишу «СТОП». Результаты измерений записать в табл. 1.
8. Определить период колебаний маятника T1
где t1 – продолжительность колебаний.
9. Снять маятник, закрепить его на второй призме П2 и определить период колебаний T2:
Если T2 > T1 , то вторую призму переместить в направлении груза, находящегося на конце стержня.
Источник
Оборотный маятник
Цель работы: определение ускорения свободного падения методом оборотного маятника, оценка результатов измерения и расчет погрешности.
Оборудование: лабораторная установка, электронный секундомер.
Теоретическое введение
Оборотный маятник представляет собой стальной стержень, на котором укреплены два массивных груза Гн и Гп. Один из них закреплен неподвижно, а второй может передвигаться по стержню в некоторых пределах и закрепляться в нужном положении. На стержне имеются также две неподвижные опорные призмы О1 и О2. Маятник может колебаться в вертикальной плоскости, опираясь нижним ребром любой из двух призм на закрепленную на стене опорную площадку ОП (рис. 1). Для этого маятник может быть снят с опорной площадки ОП, повернут на 180о и поставлен другой опорной призмой на опорную площадку.
В работе № 6 было получено
выражение для периода Т малых ко — Гн
лебаний физического маятника: О1
(1) ОП а1
Здесь Iо – момент инерции ма — С
ятника относительно оси качаний О, a а2
M – масса маятника, g – ускорение сво — О2
бодного падения, a – расстояние от оси
качаний О до центра масс С маятника.
Соотношение (1) может быть ис — Гп
пользовано для определения g в нашей
лаборатории. Для этого необходимо из-
мерить T, Iо и a и выразить через них g Рис. 1.
с помощью формулы (1). Оказывается, однако, что с высокой точностью можно измерить только период колебаний Т маятника, а величины Iо и a с достаточной точностью измерить не удается.. Например, для нахождения расстояния a от оси качаний до центра масс маятника необходимо предварительно определить положение центра масс С, что сделать точно довольно трудно.
Достоинством метода оборотного маятника для определения ускорения свободного падения является то, что Iо и a не входят в расчетную формулу для g. Перейдем к обсуждению этого метода.
Согласно теореме Гюйгенса – Штейнера, момент инерции маятника относительно оси качаний О
где Ic – момент инерции маятника относительно оси, параллельной оси качания и проходящей через центр масс С маятника, а – расстояние между осями.
Подставляя (2) в (1), получаем:
(3)
Обсудим качественно характер зависимости периода колебаний от расстояния а до оси качаний. При Т
очень малых а момент силы тяже-
сти — Mgasina (рис.1), стремящий-
ся вернуть маятник в положение
равновесия, становится очень ма-
лым и период колебаний резко
возрастает. В пределе а ® 0 мо –
ент силы тяжести равен нулю и
колебания вообще невозможны: 0 а
маятник находится в положении
безразличного равновесия (маят — Рис. 2.
ник подвешен за центр масс). Это согласуется с формулой (3): при а ® 0 период
В обратном пределе очень больших а можно пренебречь Ic по сравнению с Ma2 и рассматривать физический маятник как математический с длиной подвеса l = a. В этом случае период колебаний
При а ® ¥ период Т также неограниченно возрастает. При возрастании а период Т сначала убывает до некоторого минимального значения, а затем снова возрастает. Качественно вид зависимости Т(а) изображен на рис. 2.
Если закреплять подвижный груз Гп на различных расстояниях от конца стального стержня, по положение центра масс С маятника будет меняться, а значит, будут меняться и расстояния а1 и а2 от центра масс до призм О1 и О2. Обозначим период колебаний маятника, когда он подвешен на призме О1 , через Т(а1 ), а когда он подвешен на призме О2 – через Т(а2 ). Тогда, согласно (3) имеем:
(4)
(5)
Когда мы перемещаем подвижный груз Гп от конца стержня к опорной призме О2, центр масс С приближается в призме О1 (см. рис. 1), расстояние а1 уменьшается, расстояние а2 увеличивается, однако сумма этих расстояний все время остается постоянной и равной расстоянию между опорными призмами:
В нашей установке L = (730 ± 1) мм.
На рис. 3 показаны примерные зависимости периодов Т(а1 ) и Т(а2 ).
Видно, что при некотором положении подвижного груза эти периоды становятся равными: Т(а1 ) = Т(а2 ). В этом положении (см. (4) и (5)) необходимо, чтобы выполнялось равенство:
которое имеет место либо
при а1 = а2 , либо при )
В последнем случае
период колебаний маятника
Следовательно, ускорение свободного падения может быть определено по формуле
(8)
Как видно из (8), для нахождения g достаточно знать расстояние L между опорными ребрами призм и период колебаний маятника при таком положении подвижного груза, при котором периоды колебаний маятника в “прямом” и “перевернутом” положениях совпадают.
Измерения
Добиться полного совпадения периодов, т. е. точного равенства:
Т(а1 ) = Т(а2 ), практически очень сложно.
Целесообразно проводить измерения следующим образом.
Закрепим подвижный груз вблизи конца стального стержня. Подвесим маятник на одну призму и определим период колебаний. Не меняя положения груза, перевернем маятник, подвесим на другую призму и определим период колебаний. Пусть оказалось, например, что Т(а1 ) > Т(а2 ), что соответствует левому краю графика на рис. 3.
Передвинем подвижный груз на 1 см, закрепим его на стержне, и опять измерим периоды колебаний маятника в “прямом” и “перевернутом” положениях. Если опять оказалось, что Т(а1 ) > Т(а2 ), то продолжаем этот процесс до тех пор, пока при некотором положении подвижного груза не окажется, что Т(а1 ) станет меньше, чем Т(а2 ). Это будет соответствовать тому, что мы на рис. 3 перейдем точку пересечения графиков этих зависимостей.
Таким образом, мы локализуем точку пересечения графиков с точностью до 1 см. На этом этапе измерений период колебаний маятника в целях экономии времени можно измерять с невысокой точностью, для чего достаточно измерять время, например, 10 колебаний при использовании ручного секундомера или 50 колебаний при использовании часов с секундной стрелкой.
Далее произведем уточнение положения подвижного груза, при котором периоды совпадают. Для этого будем передвигать подвижный груз с шагом в 1мм в пределах найденного сантиметра. Таким образом, мы сможем локализовать точку пересечения графиков с точностью до 1 мм. Этот процесс уточнения можно продолжать и дальше.
Для достижения достаточной точности определения ускорения свободного падения, например: sg = (0,02 ¸ 0,03) м/с2 , необходимо найти такое положение подвижного груза, чтобы периоды совпадали с точностью до (1 ¸ 2)×10-3 с (докажите это утверждение! ). При пользовании часами, измеряющими время с точностью до 1 с, для этого придется измерить время не менее 500 колебаний; при использовании ручного секундомера, меряющего время с точностью до 0,1 с – не менее 50 колебаний. Повышать слишком сильно точность определения периода, а тем более добиваться полного совпадения периодов, нет смысла, так как расстояние а между опорными призмами нам известно в данной работе с относительной точностью Dа/а = 1/730 = 0,0014 (т. е. 0,14%) и ускорение свободного падения не может быть определено в данной работе с точностью, лучшей чем эта величина.
Добившись совпадения периодов колебаний с точностью, не хуже, чем 0,002 с, по формуле (8) определяют g.
Отметим, что все измерения периодов Т(а) следует проводить при малых угловых амплитудах, не превышающих 4 – 5о, так как только в этом случае для периода колебаний маятника справедлива формула (1).
1. Что называется моментом инерции? Что называется моментом силы?
2. Сформулируйте теорему Гюйгенса-Штейнера.
3. От чего зависит период колебаний физического маятника?
4. От чего зависит точность определения периода колебаний?
5. С какой точностью можно измерить ускорение свободного падения в лаборатории с помощью оборотного маятника?
Источник
