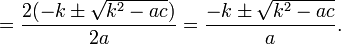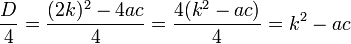Выведите формулу корней квадратного уравнения с четным вторым коэффициентом

Выведите формулу корней квадратного уравнения с четным вторым коэффициентом

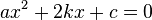
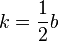
Для уравнений вида , то есть при чётном , где
вместо формулы (1) для нахождения корней можно использовать эквивалентное выражение

Действительно, подставим в вышеприведённую универсальную формулу (1) корней уравнения указанное соотношение:

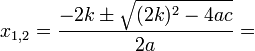
Для приведённого квадратного уравнения эта формула принимает вид:

.

Также при чётном удобнее вычислять значение не целого дискриминанта, а его четверти:

или, если уравнение приведённое:

.

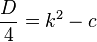
Все необходимые свойства при этом сохраняются:

0 \Rightarrow D>0″ src=»http://upload.wikimedia.org/math/6/8/e/68eda98d8feacc2fbb9ee7adae1dc95b.png»/>

(вместо знака «больше» в выражение может быть подставлены и другие знаки: «меньше» или «равно»). Подобным преобразованиям можно подвергнуть формулу для нахождения единственного корня при :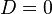

.

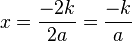
Обратите внимание, что для приведённого уравнения можно упростить расчёт следующим образом:

.

Отсюда следует важное и полезное правило: корнем приведённого уравнения с чётным вторым коэффициентом и равным нулю дискриминантом является половина второго коэффициента.

Эти выражения является более удобным для практических вычислений при чётном .

Источник

Решение квадратных уравнений
план-конспект урока по алгебре (8 класс) по теме

Скачать:

Вложение	Размер
prezentatsiya_microsoft_powerpoint_2.ppt	456 КБ
moy_urok_po_kvadr.uravn_.doc	131.5 КБ

Как сдать ЕГЭ на 80+ баллов?

Репетиторы Учи.Дома помогут подготовиться к ЕГЭ. Приходите на бесплатный пробный урок, на котором репетиторы определят ваш уровень подготовки и составят индивидуальный план обучения.

Бесплатно, онлайн, 40 минут

Предварительный просмотр:

Подписи к слайдам:

Решение квадратных уравнений

Цели урока: Повторить основную формулу решения квадратных уравнений; Вывести формулу №2; Научить применять её к квадратным уравнениям с чётным вторым коэффициентом; Познакомить с приёмами устного решения квадратных уравнений с помощью дополнительных формул; Научить применять новые формулы к решению уравнений Воспитание трудолюбия, любознательности , ответственного отношения к учёбе

Проверка домашнего задания № 542 а)5х2= 9х+2 х1,2 === 2;-0,2 б)-х2 =5х -14 =0 х1,2 === — 7; 2 в) 6х+9 =х2 х1,2 = 3 +3;3 — 3; г ) z -5 = z 2 -25 х1,2 === 5 ; — 4 г ) z -5 = z 2 -25 х1,2 === 5 ; — 4 д ) у2 =52у -576 х1,2 === 36 ; -16 е ) 15 у2 -30 =22у +7 х1,2 === -1; 2 ж ) 25 p 2 -10 p +1=0 х= = 0,2 з ) 299х2 +100х =500- 101х2 х1,2 === 1; -1 № 543 а) 25=26х-х2 х2 -26х +25 =0 Д= b 2 – 4 ac =676-100 =576; Д >0 ,2 корня : х1,2 === 25 ;1 б ) 3х2 =10 -29х 3х2 +29х -10 =0 Д= b 2 – 4 ac =841+120= 961; Д >0 ,2 корня : х1,2 === -10 ; в )у2 = 4у +96 у2 — 4у -96 =0 Д= b 2 – 4 ac =16+384= 400; Д >0 ,2 корня : х1,2 === -8 ;12 г ) 3 p 2 +3=10р 3 p 2 — 10р +3 =0 Д= b 2 – 4 ac =100-36= 64; Д >0 ,2 корня : х1,2 === 3 ; д ) х2 -20х=20х+100 х2 -40х -100 =0 Д= b 2 – 4 ac =1600+400= 2000; Д >0 ,2 корня : х1,2 === 20+10; 20 -10; е ) 25х2 -13 х =10х2 -7 15х2 -13х +7 =0 Д= b 2 – 4 ac =169 -420= -259; Д 0, то х1,2 = = , где D 1 = k 2 –ас , если D 1 Конспект урока по алгебре в 8 классе

на тему «Решение квадратных уравнений по формуле №2

с чётным вторым коэффициентом»

1. Вывести формулу корней квадратного уравнения с четным вторым

2. Продолжить формирование навыка решений квадратных уравнений .

3.Расширение знаний и навыков решения квадратных уравнений.

4.Развитие интеллекта , сознательного отношения к учебе.

I .ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ

1.В парах по заранее приготовленным заданиям на доске проверяют правильность выполненных уравнений.

Д=b 2 – 4ac=81+40=121,Д >0 ,2 корня :

Х 1,2 = ; х 1 =2; х 2 =-0,2

Д=b 2 – 4ac=25+56= 81; Д >0 ,2 корня : х 1,2 = = = — 7; 2

Д=b 2 – 4ac=35+36=72; Д >0 ,2 корня : х 1,2 = = = 3 +3 ;3 — 3 ;

Д=b 2 – 4ac=1+80=81; Д >0 ,2 корня : х 1,2 = = = 5 ; — 4

Д=b 2 – 4ac=2704 -2304=400; Д >0 ,2 корня : х 1,2 = = = 36 ; -16

е ) 15 у 2 -30 =22у +7

15 у 2 -22у -37 =0

Д=b 2 – 4ac=484 +2220=2704; Д >0 ,2 корня : х 1,2 = = = -1; 2

ж ) 25p 2 -10p +1=0

Д=b 2 – 4ac=100-100=0; Д =0 ,1 корень : х= = 0,2

з ) 299х 2 +100х =500- 101х 2

400х 2 +100х-500 =0| : 100

Д=b 2 – 4ac=1+80 =81; Д >0 ,2 корня : х 1,2 = = = 1; -1

Д=b 2 – 4ac=676-100 =576; Д >0 ,2 корня : х 1,2 = = = 25 ;1

Д=b 2 – 4ac=841+120= 961; Д >0 ,2 корня : х 1,2 = = = -10 ;

Д=b 2 – 4ac=16+384= 400; Д >0 ,2 корня : х 1,2 = = = -8 ;12

Д=b 2 – 4ac=100-36= 64; Д >0 ,2 корня : х 1,2 = = = 3 ;

д ) х 2 -20х=20х+100

Д=b 2 – 4ac=1600+400= 2000; Д >0 ,2 корня :

х 1,2 = = = 20+10 ; 20 -10 ;

е ) 25х 2 -13 х =10х 2 -7

Д=b 2 – 4ac=169 -420= -259; Д корней нет

II. УСТНЫЕ УПРАЖНЕНИЯ

1.Докажите ,что -1 является корнем уравнения : х 3 +1=0, х 2 -1=0,х 2 +х =0,х 2 +3х+2=0.

2.Укажите коэффициенты квадратного уравнения:

2х 2 -5х+10 = 0 , 2+х+х 2 =0 , х 2 +3х -0,5 =0 , 5х 2 -4х =3 , 0,5х 2 –х -3 =0 , 8х -7 =х 2

1-3х-2х 2 =0 , 11-2х 2 =4х.

3.Замените уравнение равносильным ему приведённым квадратным уравнением:

3х 2 -6х -12 =0; х 2 -3х +6=0; -х 2 +2х -2 =0; 10х 2 -20х +30 =0.

4.Имеет ли квадратное уравнение корни ; если имеет, то сколько; рациональными или иррациональными числами являются корни: 4х 2 -12х +9 =0 , 2х 2 +3х -9 =0;

5х 2 — х+2=0 ; 4х 2 +7х -1 =0; х 2 -3х +5 =0; 3х 2 +2х -2 =0; 3х 2 -11х +10=0; 25х 2 +10х+1=0

5.Подберите какие-нибудь значения с , при которых уравнение имеет корни:

х 2 -3х +с =0; 5х 2 — 2х +с =0.

III.АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ :

(проводится в виде диктанта с взаимопроверкой в парах, двое учащихся выполняют задания на отворотах доски)

1.Запишите общий вид квадратного уравнения и формулу дискриминанта:

2.При каком условии полное квадратное уравнение :

Имеет единственный корень | не имеет корней

3.Вычислите дискриминант квадратного уравнения :

3х 2 -8х — 3=0 | 2х 2 -3х -2=0

4.Решите квадратное уравнение :

х 2 -4х+9=0 | х 2 -6х+5=0

5. Подберите какое-нибудь значение с , при котором уравнение имеет корни:

х 2 -3х +с=0; | х 2 -2х+с=0.

IV. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА :

Поручить уч-ся самостоятельно изучить в течение 5 минут вывод формулы из п.21(стр.115).Затем сильный ученик выполняет вывод на доске , дети записывают в тетради. Для квадратных уравнений, у которых второй коэффициент является четным числом , формулу корней удобно записывать в другом виде:

D=b 2 – 4ac=4k 2 -4ас =4(k 2 –ас),D1 = k 2 –ас; если D1>0, то

х 1,2 = = = , где D1 = k 2 –ас ,

Привести вторую запись данной формулы при условии , если в приведенном квадратном уравнении второй коэффициент чётный :

х 2 +2kх +с =0; , где b =2k , то есть : х 1,2 = (формулаII)

Для быстрого запоминания формулы привожу стихотворные строки:

« …б со знаком взяв обратным , мы на два его поделим ,

И от корня аккуратно знаком „минус-плюс” отделим ,

а под корнем очень кстати – половина б в квадрате, минус це (с) и вот решенье небольшого уравненья»

V. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО:

Решить на доске : №539 (а,б,в,ж)

а )3х 2 -14х+16=0 б) 5х 2 -16х+3=0

Д 1 =7 2 -3·16=1, х 1,2 = = 2 ;2 Д 1 =8 2 -15=49, х 1,2 = = ;3

в ) х 2 +2х-80=0 ж)7z 2 -20z+14=0

х 1,2 = -1 =-1 9 =8; -10 Д 1 =10 2 -7∙14=2, х 1,2 = .

Обучающая самостоятельная работа :№539 (г, д , е, з) с последующей проверкой. Ответы :

Источник

Вывод формулы корней полного квадратного уравнения. Решение приведенных квадратных уравнений и уравнений с четным вторым коэффициентом

Разделы: Математика

Устный счет:

1. При каком значении Х , выражение принимает минимальное значение

а) ; б)
2. Зависимость y(x) выражается формулой y = 13x + 1 выразить x(y)

3. Не решая уравнения, определить, равносильны ли они:

4. Выделить полный квадрат:

5. Вычислить пары чисел , удовлетворяющих условиям

а) m + n = 4 mn = 4

б) m + n = –3 mn = –18

1. Какое уравнение называется полным?
2. Что такое корни квадратного уравнения?
3. Сколько корней может иметь квадратное уравнение?

Теорема. Квадратное уравнение не может иметь более двух различных корней.

Доказательство:

Предположим, что уравнение три различных корня:

Если уравнение имеет корень, то после подстановки его в уравнение получится верное числовое равенство:

(1)
(2)
(3)

из (2) отнимаем (1)

–

_____________________

В каком случае произведение равно 0?

Так как = > 0 = > a+ b = 0. (4)

–

_________________

= > a+ b = 0 (5)

–

________________

а0 = > = > ,
а по условию пришли к противоречию.

Давайте решим уравнение:

Самостоятельно:

a)

Вместе:

б)

Нравится ли этот способ? Нет! Тогда будем рассуждать иначе:

(формулу для нахождения корней квадратного уравнения учить проговаривать словами).

– дискриминант квадратного уравнения.

По теореме, доказанной нами , уравнение не может иметь более двух корней.

Количество корней зависит от D.

1). D > 0
2). D = 0

Источник