Выведите формулу для расчета энергии упругой деформации

Сопромат .in.ua

изучаем сопротивление материалов

Потенциальная энергия упругой деформации

Рассмотрим один подход к определению потенциальной энергии упругой деформации.

Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу А на соответствующих перемещениях. Одновременно с этим в упругом теле накапливается потенциальная энергия его деформирования U. При действии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде:

При действии статических нагрузок (или если сила прикладывается достаточно медленно, т. е. ее скорость приложения стремится к нулю) К = 0, следовательно,

Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформации. При разгрузке тела производится работа за счет потенциальной энергии деформации, накопленной телом. То есть, упругое тело является аккумулятором энергии. Это свойство упругого тела широко используется, например, в заводных пружинах часовых механизмов, в луке и т.д. Для вывода необходимых расчетных зависимостей потенциальной энергии деформации рассмотрим простейший случай — растяжение стержня.

На рисунке изображен растягиваемый силой F стержень, удлинение которого соответствует отрезку Δl, а ниже показан график изменения величины удлинения стержня Δl в зависимости от силы F. В соответствии с законом Гука этот график носит линейный характер (стержень растягивается в пределах упругих деформаций).

Пусть некоторому значению силы F соответствует удлинение стержня Δl. Дадим некоторое приращение силе dF. Соответствующее приращение удлинения составит d (Δl ). Тогда элементарная работа на этом приращении удлинения составит:

dA = (F + dF)·d (Δl ) = F·d (Δl ) + dF· d (Δl )

вторым слагаемым, в силу его малости, можно пренебречь, и тогда

Полная работа равна сумме элементарных работ, тогда, при линейной зависимости “нагрузка — перемещение”, работа внешней силы F на перемещении Δl будет равна площади треугольника ОСВ

Для однородного стержня с постоянным попе­речным сечением и при F = const, зная из закона Гука что Δl = FL/EA (здесь и далее_A_ – площадь сечения), получим:

Здесь
U – потенциальная энергия упругой деформации
F – нагрузка
E – Модуль Юнга
L – длина
A – площадь сечения

Для оценки энергоемкости материала используют удельную потенциальную энергию, накапливаемую в единице объема: u= U/V, где V— объем стержня (V=L·A). Зная, что σ=F/A= Eε, для стержня (напряжения σ и деформации ε распределены по объему тела V равномерно) можем записать

Потенциальную энергию упругой деформации можем выразить через удельную потенциальную энергию:
$$U=\int_udV$$

Источник

Сила упругости

О чем эта статья:

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Деформация

Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил

Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.

Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.

На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.

По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:

• Деформация растяжения
• Деформация сжатия
• Деформация сдвига
• Деформация при кручении
• Деформация при изгибе

Сила упругости: Закон Гука

Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.

Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, про­порциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Закон Гука

Fупр = kx

Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]

Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.

m = 300 г = 0,3 кг

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

F = mg = 0,3*10 = 3 Н.

Тогда из Закона Гука выразим модуль удлинения лески:

Выражаем модуль удлинения:

Подставим числа, жесткость лески при этом выражаем в Ньютонах:

x=3/(0,3 * 1000)=0,01 м = 1 см

Ответ: удлинение лески равно 1 см.

Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

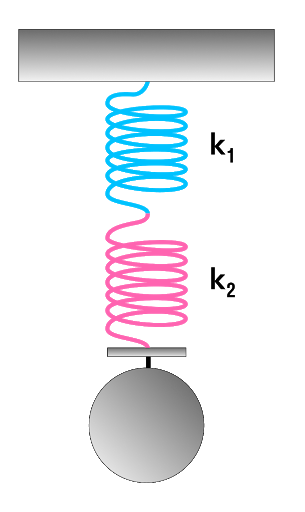
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Коэффициент жесткости при последовательном соединении пружин

1/k = 1/k₁ + 1/k₂ + … + 1/k_i

k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Коэффициент жесткости при параллельном соединении пружин

k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

Задачка

Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.

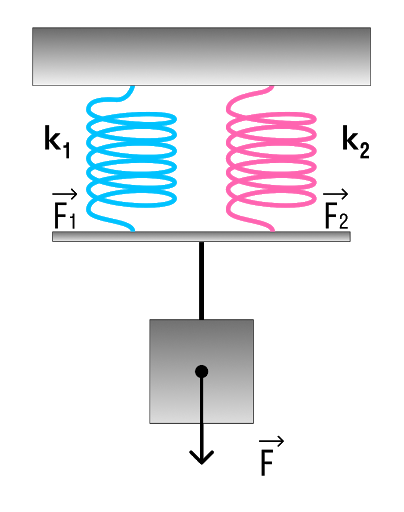
При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

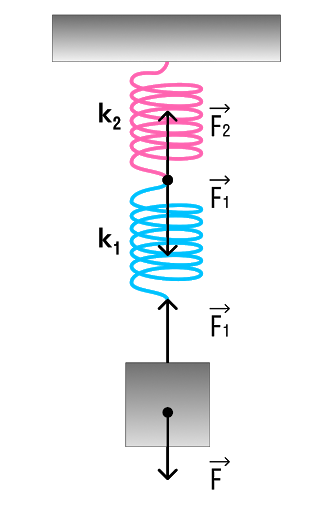
При последовательном соединении общая жесткость двух пружин

1/k = 1/k₁ + 1/k₂ + … + 1/k

1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015

k = 1000/15 = 200/3 ≃ 66,7 Н/м

График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

Задачка 1

Определите по графику коэффициент жесткости тела.

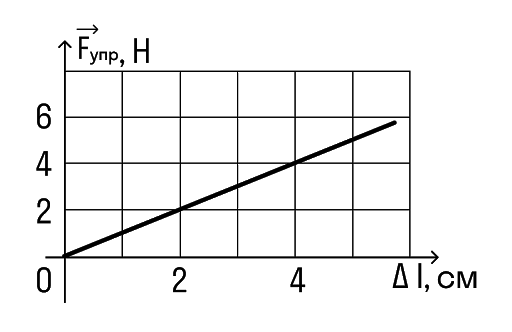
Решение:

Из Закона Гука выразим коэффициент жесткости тела:

Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Задачка 2

На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.

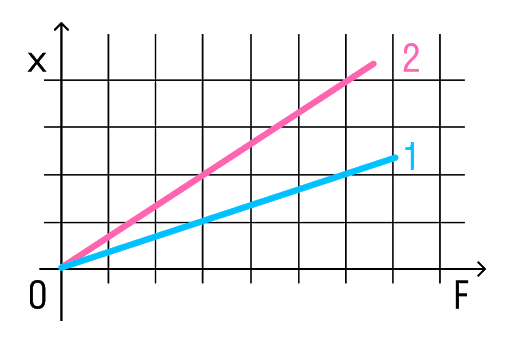
Решение:

Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.

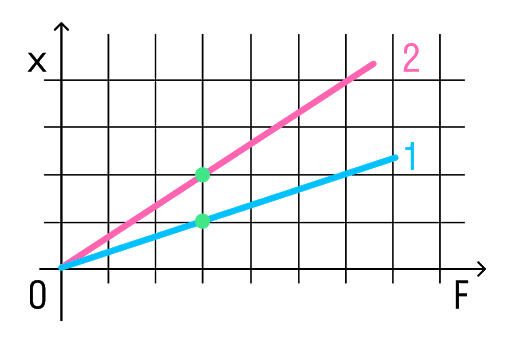
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Потенциальная энергия растянутой пружины: формула и её объяснение

Содержание:

Пружина – механизм, способный совершать работу и накапливать ее с целью отдать. Этот запас называется потенциальная энергия пружины, формулу и определение которой рассмотрим в статье. Научимся вычислять её.

Энергия упругой деформации

Рассмотрим, как найти потенциальную энергию растянутой пружины, что та способна совершить, принимая прежнее состояние. Предположим, одним концом она закреплена к опоре, ко второму крепится груз. Над ним совершается механическая работа. Учтём, что действующая на тело сила – постепенно снижается пропорционально растяжению. То есть, чем сильнее сжимается растянутая пружина либо растягивается сжатая (в зависимости от её типа), тем ниже её энергетический запас.

Если изначальное растяжение равно l (измеряется от исходного, состояния покоя), то исходную силу упругости вычисляют по формуле:

F = kl, k – коэффициент пропорциональности либо жёсткость.

Вследствие деформации тела значение нелинейно убывает от kl до ноля. Средний показатель вычисляется по формуле: F_ср = kl : 2.

Отсюда проделанная работа равняется произведению силы упругости на пройденное грузом расстояние:

A = (kl : 2) * l = kl 2 : 2, значит E_п= kl 2 : 2.

Аналогичное выражение и для сжатого тела.

Здесь E выражается коэффициентом жёсткости пружины и её линейным растяжением, возникающим вследствие деформации.

Из первой формулы F = kl выразим l = F : k. Формула потенциальной энергии растянутой пружины примет вид:

Выражение показывает: в случае прикладывания одинаковых усилий для растяжения либо сжатия пружин им придаётся разная E_п. Причина – они обладают различной жёсткостью. Чем выше прочность – меньше упругость, тем ниже её Eп и наоборот. Для наглядности: мягкий амортизатор, сжимаясь, протянет подвешенный или прицепленный груз дальше, чем жёсткий, при этом совершит большую работу.

На практике выявленная закономерность применяется при конструировании систем амортизации: рессор, шасси. Мягкие амортизаторы в шасси лучше предохраняют самолёт от повреждений во время приземления, чем жёсткие, а при слабо накачанных шинах неровности дороги ощущаются слабее.

Источник