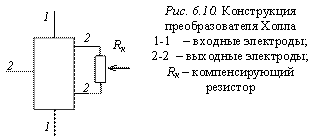Выведите формулу для эдс холла

Одним из проявлений магнитной составляющей силы Лоренца в веществе служит эффект, обнаруженный в 1879 г. американским физиком Э.Г. Холлом (1855–1938). Эффект состоит в возникновении на боковых гранях проводника с током, помещенного в поперечное магнитное поле, разности потенциалов, пропорциональной величине тока I и индукции магнитного поля В.

Рассмотрим эффект, обусловленный действием лоренцевой силы на свободные заряды в проводнике. Представим себе проводник с током I в виде плоской ленты, расположенной в магнитном поле с индукцией , направленной от нас (рис. 2.19).

В случае изображенном на рис. 2.19, а, верхняя часть проводника будет заряжаться отрицательно, в случае 2.19, б – положительно.

Это позволяет экспериментально определить знак носителя заряда в проводнике.

При равной концентрации носителей заряда обоих знаков возникает холловская разность потенциалов, если различна подвижность, т.е. дрейфовая скорость носителей заряда.

Подсчитаем величину холловской разности потенциалов (U_х).

Обозначим: E_x – напряженность электрического поля, обусловленного ЭДС Холла, h – толщина ленты проводника.

(2.10.1)

Перераспределение зарядов прекратится, когда сила qE_x уравновесит лоренцеву силу, т.е.

или

Плотность тока , отсюда . Тогда .

(2.10.2)

где – коэффициент Холла.

Исследования ЭДС Холла привели к удивительным выводам. Металлы могут обладать проводимостью р-типа (Zn, Cd – у них дырки более подвижные, чем электроны). Это металлы с чуть перекрывающимися знаками, т.е. полуметаллы.

Из формулы (2.10.2) можно найти число носителей заряда:

(2.10.3)

Итак, измерение холловской разности потенциалов позволяет определить:

· знак заряда и тип носителей;

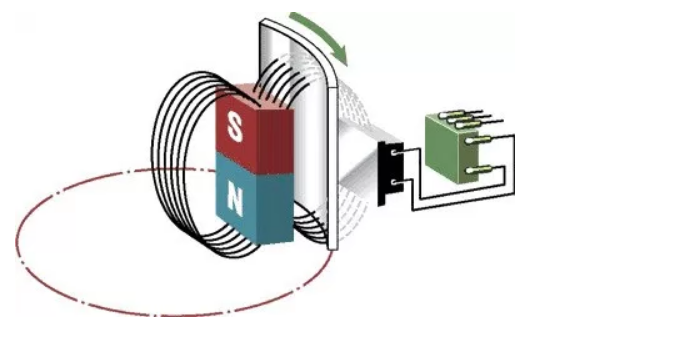
На рисунке 2.20 показана установка для исследования магнитного поля длинного соленоида с помощью датчика Холла.

Источник

Теория метода. ЭДС Холла находится по формуле:

ЭДС Холла находится по формуле:

где R – постоянная Холла, j – плотность тока, текущего через образец, b – толщина образца, а – его ширина, В – индукция магнитного поля, I – сила тока в образце (j=I/S=I/ab).

Для двух разных значений силы тока, текущего через датчик Холла, ЭДС Холла можно найти по формулам:

Вычитая из второго выражения первое, получим:

Если построить график зависимости U_H от I, то он будет выражаться прямой линией, и К= Δ U_H/Δ I=RB/a будет являться угловым коэффициентом для этой прямой.

Если определить К для разных значений индукции В и построить график зависимости К от В, то этот график также будет выражаться прямой (зависимость прямо пропорциональная). Угловой коэффициент для этого графика:

β= ΔК/ΔВ=R/a.Измерив β, можно найти постоянную Холла по формуле:

R=βa.(1)

Зная постоянную Холла, можно определить концентрацию носителей по формуле:

n=1/Re(2)

где e – элементарный заряд.

Описание установки

Установка состоит из объекта исследования и измерительного устройства.

Объект исследования содержит электромагнит и датчик Холла.

На передней панели измерительного устройства имеются следующие органы управления и индикации:

— кнопки НАПРАВЛЕНИЕ и ТОК «+», «- « задают значение тока через датчик Холла и через электромагнит (для увеличения значения тока нажимается «+», для уменьшения – «-«; нажатием кнопки СБРОС значения тока сбрасываются и одновременно меняется полярность, то есть направление соответствующего тока.

-ЭЛ.МАГНИТ-ДАТЧ.ХОЛЛА включает индикацию тока электромагнита или датчика Холла;

-табло мА и мВ показывают значения тока через датчик Холла или электромагнит (см.индикацию) и ЭДС Холла.

Порядок выполнения работы

1. Включите установку.

2. Выберите полярность источников питания для датчика Холла и электромагнита нажатием соответствующих кнопок.

3. Кнопкой ЭЛ.МАГНИТ-ДАТЧ.ХОЛЛА включите индикацию тока электромагнита и задайте ток электромагнита i=3,2 мА. Переключите эту кнопку на индикацию тока датчика Холла и, увеличивая ток с интервалом 0,5 мА, измерьте значения ЭДС Холла для 8-10 значений силы тока I через датчик Холла. Нажатием кнопки «СБРОС» измените направление тока через датчик (или через электромагнит – по указанию преподавателя) и повторите измерения.

Проведите аналогичные измерения еще для 2-х значений тока через электромагнит (задаются преподавателем в интервале от 3,2 мА до 6 мА ). Результаты измерений занесите в таблицу 1.

Источник

Эффект Холла и его применение

После проведения эксперимента в 1879 году Эдвином Холлом при пропускании магнитного потока через тонкую пластину из золота было обнаружено возникновение на краях пластины разности потенциалов, то есть образовался эффект Холла.

В чем заключается эффект Холла

При помещении в магнитное поле пластины-проводника или полупроводника под 90 ° к направлению силовых линий магнитного потока произойдет перемещение электронов по поперечине пластины под действием силы Лоренца. Их направление зависит от того, в какую сторону идет сила тока и силовые линии магнитного потока. Иначе говоря, (ЭХ) эффект Холла – это частный случай действия силы Лоренца, то есть действия магнитного поля на заряженную частицу.

Это можно рассмотреть на простейшем примере.

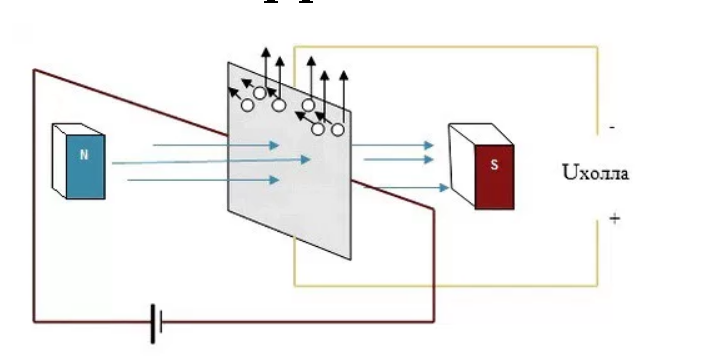
Если представить расположенную к нам торцом пластину, то ее кромка направлена вниз. Она сделана из металла, оба торца подключены к источнику питания, задний из которых на минус, передний на плюс.

Данный случай говорит о том, что электрический ток будет протекать по направлению к наблюдателю. Справа и слева от пластины располагаются два магнита. Правый из них обращен к пластине северным полюсом, левый – южным. Делаем вывод, что данный случай показывает направление силовых линий магнитного поля справа налево, так как они всегда выходят из северного полюса и входят в южный. Силовые линии отклоняют электроны, которые проходят по пластине к ее верхней кромке.

При изменении направления тока в пластине при помощи перемены местами проводников мы сможем наблюдать отклонение электронов вниз. Если направление не менять, а только лишь полюса магнитов, электроны начнут сдвигаться вниз. Когда применяются оба направления, сила Лоренца произведет их перемещение вверх.

Очевидно, что одна из кромок накапливает отрицательный заряд под действием силы Лоренца, на другая на противоположной стороне – положительный. Это говорит о наличии разности потенциалов между ними, то есть электрического напряжения. Увеличение этой разности будет происходить до тех пор, пока не уравновесит силу Лоренца.

Возникновение разности потенциалов в таких случаях, получило название напряжения Холла, которое можно рассчитать, используя формулу:

U х о л л = — I B e t , где I является силой тока, B – вектором магнитной индукции, e – зарядом электрона, p – количеством электронов в единице объема, t – толщиной пластины.

Аномальный ЭХ

Имеются случаи, когда ЭХ может быть обнаружен в пластине без пропускания через нее магнитного потока. Это возможно при нарушении симметрии по отношению к обращению времени в системе. В частности, аномальный ЭХ способен проявляться в намагниченных материалах.

Квантовый ЭХ

Двумерные газы со средним расстоянием между частицами, уменьшенным до значения длины де Бройля на зависимости поперечного сопротивления к воздействию магнитного поля, подвержены возникновению плато сопротивления в поперечине. ЭХ квантуется только в сильных магнитных полях.

Магнитные потоки, обладающие больше силой индукции, имеют дробный квантовый ЭХ. Он взаимосвязан с перестроением внутренней структуры двумерной электронной жидкости.

Спиновый ЭХ

СЭХ можно наблюдать на не намагниченных проводниках, которые не переместили в поле действия силовых линий магнита. Суть эффекта – отклонение электронов с антипараллельными спинами к противоположным краям пластины.

Применение эффекта Холла

Применение метода Холла связано с изучением особенностей полупроводников. С его помощью стало возможным вычисление количества носителей заряда на единицу объема, а также их подвижность. При его использовании реально отличить электрон от квазичастицы с положительным зарядом.

ЭХ всегда считался основой для разработки датчиков Холла. Аппаратура предназначена для измерения напряженности магнитного поля. Их используют для построения моторов со следящим приводом. В моторах они исполняют роль датчика обратной связи. Они способны измерить угол поворота вала мотора.

Датчики Холла устанавливают в электростартерах ДВС, охлаждающих системах ПК, навигационных системах мобильных телефонов, в измерительных приборах для вычисления количества заряда.

Источник

Выведите формулу для эдс холла

Эффект, открытый американским физиком Эдвином Гербертом Холлом в 1879 году, заключается в явлении возникновения поперечной разности потенциалов в полупроводнике, по которому протекает электрический ток и существует магнитное поле Н, перпендикулярное направлению тока.

Физическая природа эффекта Холла заключается в том, что на движущийся носитель тока в магнитном поле с индукцией В действует сила Лоренца

, Н, (6.11)

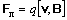
где v –скорость носителя; q – его заряд.

Направление силы Лоренца определяется правилом левой руки. Если проводник n -типа проводимости, то электроны будут смещаться влево к внешней стороне пластины, заряж ая её о трицательно (рис. 6.8).

В полупроводника p -типа проводимости при том же направлении тока сила Лоренца будет смещать дырки в том же направлении. При этом левая внешняя сторона пластинки зарядится положительно.

Если угол между вектором скорости носителей v и вектором магнитной индукции B равен 90 о , то величина силы Лоренца рассчитывается по формуле

где v – средняя дрейфовая скорость носителей заряда, м / c .

Электрическое поле между поперечными гранями пластинки равно

, В/ м , (6.13)

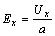
где U _х » (0,6…1)·10 -4 В — разность потенциалов между поперечными гранями пластинки, называемая эдс Холла; а – ширина пластинки.

Поле Е_х действует на электроны с силой F =- qE _х , направленной против силы Лоренца F _л. При выполнении условия F _л= F поперечное электрическое поле уравновешивает силу Лоренца и дальнейшее накопление электрических зарядов на боковых гранях пластины прекращается. Тогда из равенства qvB = qE _х следует E _х= vB . Дрейфовая скорость носителей тока определяется из выражения

, (6.14)

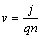
где j – плотность тока, А/м 2 , n – концентрация электронов, м -3 ,

Тогда выражение для поля Е_х приобретает вид

. (6.15)

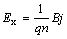
Умножив обе части равенства (6.15) на ширину пластинки а, получаем формулу для эдс Холла

, В. (6.16)

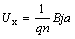
Формула (6.16) обычно записывается в виде

, (6.17)

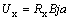
где 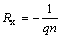– коэффициент Холла, м 3 /Кл.

С учетом разброса средней скорости дрейфа электронов в полупроводнике значение коэффициента Холла определяется из выражения

, (6.18)

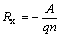
где А =1,18 для полупроводников с преимущественным рассеянием носителей заряда на тепловых колебаниях кристаллической решетки; А=1,93 при рассеянии на ионизированных примесях.

Для дырочных полупроводников коэффициент Холла рассчитывается по формуле

, (6.19)

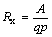
где q и p –заряд и концентрация дырок, соответственно.

При смешенной электронно-дырочной проводимости величина коэффициента Холла рассчитывается по формуле

, (6.20)

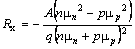
где μ _n и μ _p – подвижности электронов и дырок, соответственно.

Из формулы (6.20) следует, что в собственных полупроводниках при выполнении условия n_i = p_i значение коэффициента Холла равно

. (6.21)

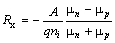
6.2.2. Преобразователи Холла

Это гальваномагнитные полупроводниковые приборы, основанные на использовании эффекта Холла.

ЭДС преобразователя Холла конечной длины рассчитывается по формуле

, (6.22)

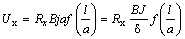
где J – ток через преобразователь , А; δ – толщина преобразователя, м; l – длина преобразователя; а – ширина преобразователя; 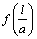— поправочная функция, график которой приведен на рис. 6.9.

Материалом для преобразователя Холла служит монокристаллическая пластинка из Ge или InSb . Эти материалы характеризуются высокой подвижностью электронов. Также используются тонкие пленки с толщиной δ=0,01…0,1 мкм, нанесенные на диэлектрическую подложку методом испарения в вакууме. Материалами служат HgSe , HgTe , сплавы HgSe — HgTe , в которых подвижность электронов достигает значения 1 м 2 / (В·с). Конструкция преобразователя Холла показана на рис. 6.10. Для устранения неэквипотенциальности выходных электродов 2-2 в схеме подключения преобразователя предусмотрен переменный резистор R _к. Предельная частота работы преобразователей Холла достигает 10…100 МГц.

Поскольку величина ЭДС Холла U _х пропорциональна произведению B · J , то преобразователи Холла применяют для измерения магнитных полей и токов, в перемножающих аналоговых устройствах, в схемах модуляторов и детекторов, в качестве анализаторов спектра сигналов.

Основными параметрами преобразователей Холла являются следующие .

1. Входное сопротивление 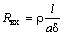– это сопротивление между входными электродами (1-1 на рис. 6.10), Ом.

2. Выходное сопротивление, R _вых, — сопротивление между выходными электродами, Ом.

3. КПД преобразователя Холла, 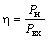, — отношение отдаваемой, P _н, и подводимой мощности, P _вх.

4. Коэффициент передачи, 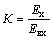, — это отношение напряженности поля ЭДС Холла, Е_х, к напряженности поля Е_вх между входными электродами.

5. Максимально допустимый ток через преобразователь, 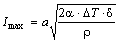, где а –ширина преобразователя, м; α – коэффициент теплоотдачи с поверхности преобразователя, Вт/(м 2 К); Δ Т » 50 К – температура перегрева преобразователя; δ – толщина преобразователя, м; r — удельное электросопротивление полупроводника, Ом·м.

6. Максимальная ЭДС Холла, U _х _max = R _x BI _max , — значение ЭДС Холла при заданной индукции магнитного поля B при протекании через датчик максимально допустимого тока I _max , В.

7. Вольтовая чувствительность 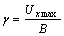, В /Т .

6.2.3. Биполярный магнитотранзистор

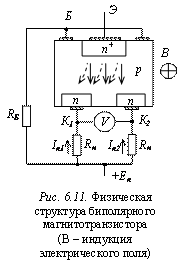
Это транзистор, в котором используется зависимость его характеристик и параметров от магнитного поля. Для увеличения чувствительности к магнитному полю биполярные транзисторы выполняют с двумя коллекторными переходами (рис.6.11). Поток магнитной индукции B отклоняет носители тока (электроны) от одного коллектора к другому. Между коллекторами возникает разность потенциалов

Биполярные магнитотранзисторы имеют вольтовую чувствительность в 100…1000 раз больше магнитной чувствительности преобразователя Холла.

Источник