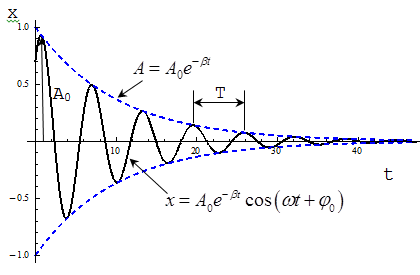
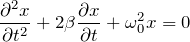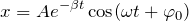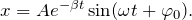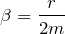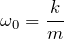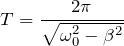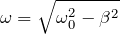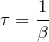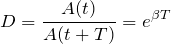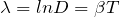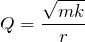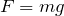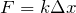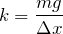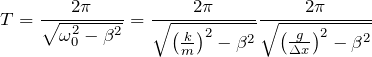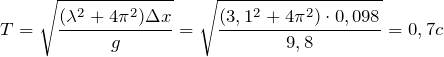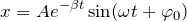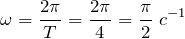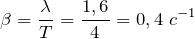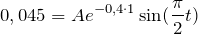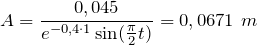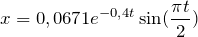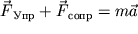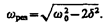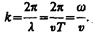Уравнение затухающих колебаний
Затухание колебаний
Свободные колебания в реальных условиях не могут продолжаться вечно. Для механических систем всегда имеет место сопротивление среды, вследствие чего энергия движения объекта рассеивается при трении. В электромагнитных контурах колебания затухают за счет сопротивления проводников.
Уравнение затухающих колебаний
Уравнение затухающих колебаний описывает движение реальных колебательных систем. В дифференциальной форме оно записывается следующим образом:
Из этого выражения можно получить еще одну каноническую форму:
либо
Здесь x и t – координаты пространства и времени, А – первоначальная амплитуда. 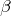
Чем больше сопротивление среды, тем больше энергии рассеивается при вязком трении. И наоборот – чем больше масса (а значит, инерционность) тела, тем дольше оно будет продолжать движение.
Циклическая частота свободных колебаний (такой же системы, но без трения) 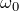
Строго говоря, в случае затухающих колебаний нельзя говорить про период – время между повторяющимися движениями системы постоянно увеличивается. Однако если колебания затухают медленно, для них с достаточной точностью можно определить период Т:
Циклическая частота затухающих колебаний
Еще одна характеристика затухающих колебаний – циклическая частота:
Время релаксации – это коэффициент, показывающий, за какое время амплитуда колебаний уменьшится в е раз:
Отношение амплитуды изменяющейся величины в двух последовательных периодах называют декрементом затухания:
Эту же характеристику при расчетах часто представляют в виде логарифма:
Добротность Q характеризует, насколько силы упругости системы превышают силы сопротивления среды, препятствуя диссипации энергии:
Примеры решения задач
| Задание | После того, как к пружине подвесили груз, она растянулась на 9,8 см. Пружина колеблется в вертикальном направлении, 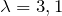 . Определить период колебаний. . Определить период колебаний. |
| Решение | Так как пружина растягивается под весом, то на нее действует сила тяжести: |
Силе тяжести противодействует сила упругости пружины:
Из двух выражений найдём коэффициент упругости:
Подставим коэффициент упругости в формулу для периода затухающих колебаний:
Зная, что логарифмический декремент затухания 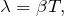
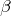
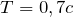
| Задание | Затухающие колебания характеризуются следующими параметрами: период 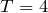 с, логарифмический декремент затухания с, логарифмический декремент затухания 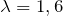 . В начальный момент отклонения фазы не было. Когда система прошла четверть периода, отклонение точки составило 4,5 см. Получить уравнение данного колебания, а также график. . В начальный момент отклонения фазы не было. Когда система прошла четверть периода, отклонение точки составило 4,5 см. Получить уравнение данного колебания, а также график. |
| Решение | Используем уравнение затухающих колебаний в каноничном виде: |
Так как отклонения фазы в момент t = 0 не было, то второе слагаемое в аргументе косинуса равно нулю.
Определим циклическую частоту:
Найдем коэффициент затухания:
Подставим в каноничное уравнение найденные параметры, а также отклонение точки в момент времени 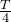
Тогда уравнение для данных колебаний примет окончательный вид:
По нему рассчитаем значения х для моментов времени до t = 3T = 12 c включительно и построим график.
Источник
Выведите дифференциальное уравнение затухающих гармонических колебаний и запишите его решение. Дайте определение логарифмического декремента затухания.
Пусть в системе действует сила вязкого трения, т. е. сила направленная против скорости движения груза, модуль которой прямо пропорционален скорости (см. рис. 1.2.1). 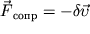

Запишем уравнение движения груза, составленное по 2-му закону Ньютона:
Подставим выражения для сил, тогда 
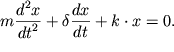
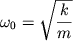
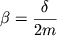
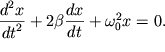
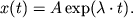
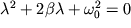


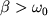

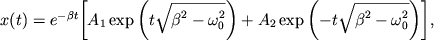
т.е. получаем затухающее движение. Если 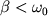
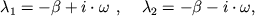
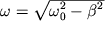
Логарифмический декремент затухания ϴ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз. 
27. Какие колебания называют вынужденными? Запишите дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Выведите формулу для расчета резонансной частоты.
Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. Внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.
Линейное неоднородное дифференциальное уравнение: 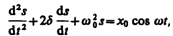
Решение уравнения равно сумме общего решения 
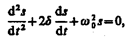
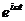
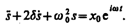
Подставляя выражение для s и его производных 

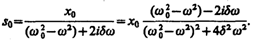
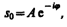


Следовательно, решение уравнения (147.6) в комплексной форме примет вид
Его вещественная часть, являющаяся решением уравнения (147.5), равна 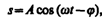
где А и j задаются соответственно формулами (147.8) и (147.9).
Таким образом, частное решение неоднородного уравнения (147.5) имеет вид
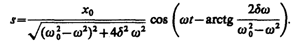

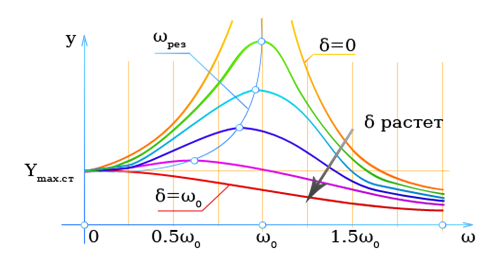
РЕЗОНАНС — частотно-избирательный отклик колебат. системы на периодич. внеш. воздействие, при к-ром происходит резкое возрастание амплитуды стационарных колебаний. Наблюдается при приближении частоты внеш. воздействия к определённым, характерным для данной системы значениям. В линейных колебат. системах число таких резонансных частот соответствует числу степеней свободы и они совпадают с частотами собственных колебаний. В нелинейных колебат. системах, реактивные и диссипативные параметры к-рых зависят от величины стороннего воздействия, Р. может проявляться и как отклик на внеш. силовое воздействие, и как реакция на периодич. изменение параметров. В строгом значении термин «Р.» относится лишь к случаю силового воздействия.
Из формулы 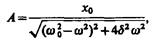
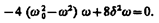

28. Какое явление называют резонансом? При каких колебаниях имеет место это явление? Получите формулу, связывающую резонансную частоту с собственной частотой и коэффициентом затухания колебательной системы. Начертите резонансные кривые для различных значений коэффициента затухания.
Определение и вывод в 27.
29. Что такое волна? Уравнение бегущей плоской гармонической волны.
Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры [1] ».
Уравнение колебаний частиц, лежащих в плоскости х, имеет вид 
откуда следует, что x(х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то
В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид 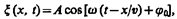

где А = const — амплитуда волны, w — циклическая частота, j0 — начальная фаза волны, определяемая в общем случае выбором начал отсчета х и t, [w (t—x/v)+ j0] — фаза плоской волны.
30. Что называют волной? Продольные и поперечные волны. Запишите волновое уравнение и уравнение плоской гармонической бегущей волны. Различаются ли уравнения для продольной и поперечной волн? Дайте определения длины волны и волнового числа.
Волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины, например, плотности вещества, напряжённости электрического поля, температуры. Более правильное определение: Волна — это явление распространения в пространстве с течением времени возмущения физической величины.
Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны.
Волновое: Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных 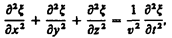
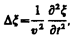

Уравнение плоской волны: В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид
Длина волны: Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l (рис. 220). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е. 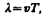
Волновое число: величина, связанная с длиной волны λ соотношением: k = 2π/λ (число волн на длине 2π). В спектроскопии В. ч. часто называют величину, обратную длине волны (1/λ).Для характеристики волн используется волновое число
31. Уравнение плоской гармонической волны. Фазовая и групповая скорость волны. Получите выражение, связывающее фазовую и групповую скорости.Уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид 
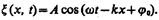
Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx. Основываясь на формуле Эйлера 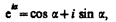
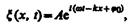
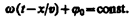


Групповая скорость: За скорость распространения этой негармонической волны (волнового пакета) принимают скорость перемещения максимума амплитуды волны, рассматривая тем самым максимум в качестве центра волнового пакета. При условии, что tdw —xdk = const, получим
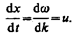
Связь: Рассмотрим связь между групповой 
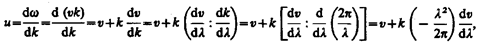
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник