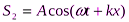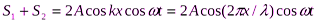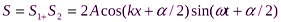Условия возникновения пучностей стоячей волны вывести координаты пучностей
Механические колебания, возникшие в какой-либо точке упругой среды, передаются другим точкам, вызывая смещение их из положения равновесия. Процесс распространения колебаний в среде называется механической волной. При этом колеблющиеся частицы не перемещаются с распространяющимся волновым процессом, а колеблются около равновесных положений. В продольной волне колебание частиц происходит в направлении распространения волны, а в поперечной они перпендикулярны направлению распространения колебаний. Поперечность или продольность волн определяется упругими свойствами среды. В жидкостях и газах распространяются только продольные механические волны, так как в них не возникают упругие силы, стремящиеся возвратить сдвинутый слой в положение равновесия. В твердых телах могут распространяться и продольные, и поперечные механические волны.
Под скоростью распространения волны (скоростью звука) понимают фазовую скорость, то есть скорость распространения данной фазы колебания, например, максимума смещения точки. Рассмотрение динамики волнового процесса позволяет получить теоретические выражения для фазовой скорости различных волн. Так, для продольных волн скорость обратно пропорциональна корню квадратному из коэффициента упругости среды и ее плотности :
Приближенно это выражение может быть заменено следующим:
где — модуль Юнга среды.
Расстояние, на которое распространяется данная фаза колебаний за период, называется длиной волны . Ее можно определить также как наименьшее расстояние между точками, колеблющимися в одинаковых фазах.
Фазовая скорость и длина волны связаны простым соотношением:
где — период колебаний источника и точек среды.
где — частота колебаний.
Из этих выражений можно определить на опыте фазовую скорость волны. Для этого нужно измерить длину волны и частоту или период колебаний.
Смещение точек бегущей волны является функцией ее координаты и времени . Уравнение плоской гармонической бегущей волны, распространяющейся в положительном направлении оси , имеет вид:
где — амплитуда колебаний; — круговая частота: ; — волновое число:
При наложении двух встречных бегущих плоских волн с одинаковыми амплитудами образуются стоячие волны с характерными точками-узлами и пучностями смещений.
Уравнение стоячей волны можно получить, если сложить левые и правые части двух уравнений:
где — смещение точек прямой, а — обратной или отраженной от препятствия волны. Получается следующее выражение:
Так смещаются со временем точки в стоячей волне.
Множитель показывает, что в точках среды возникают колебания той же частоты, что и встречных волн.
Модуль множителя , не зависящий от времени, называется амплитудой результирующего колебания. Как видно, она зависит от координаты точки.
В некоторых точках амплитуда стоячей волны равна сумме амплитуд обоих слагаемых колебаний. Такие точки называются пучностями . Координаты их можно найти из условия:
в этих точках . Координаты пучностей:
В узлах амплитуда результирующего колебания всегда равна нулю. Условие образования узлов:
отсюда можно найти координаты узлов:
Нетрудно показать, что расстояние между двумя соседними пучностями или узлами стоячей волны равно половине длины волны:
а расстояние узла от ближайшей пучности равно .
Это обстоятельство позволяет определить на опыте длину волны, а затем и ее скорость из выражения (42) и (43). Для этого нужно сделать видимыми или слышимыми пучности стоячей волны.
Стоячие волны образуются обычно при интерференции бегущей вперед и отраженной волн. На границе отражения может оказаться узел или пучность в зависимости от соотношения плотностей сред. Если среда, от которой происходит отражение, более плотная, чем среда, в которой распространяется волна, на границе сред получается узел; в противном случае — пучность.
Рассмотрим два случая образования стоячих волн, которые используются в этой работе.
Пусть имеется труба, закрытая с одного конца. Если к отверстию поднести источник звука, то в столбе воздуха, находящегося в трубе, возникнут колебания с частотой источника.
Всякий раз, когда частота вынужденных колебаний будет практически совпадать с собственной частотой воздушного столба, будет наблюдаться явление резонанса. Собственные частоты колебаний воздушного столба определяются его длиной и скоростью распространения звука в воздухе . Теоретические расчеты показывают, что собственные частоты воздушного столба в случае, когда радиус его мал по сравнению с длиной, могут быть вычислены так:
Схематически образующиеся стоячие волны можно изобразить так:
Если частота колебаний источника постоянна, явление резонанса наблюдается при плавном изменении длины воздушного столба всякий раз, когда на длине его укладывается нечетное число четвертей длин волн:
Из этого выражения видно, что наименьшая разность длин воздушного столба, при которых последовательно наблюдается явление резонанса, равна половине длины волны. Это свойство используется в работе для расчета длины волны и скорости звука в воздухе.
Если обе границы твердого тела (стержня, струны и пр.) находятся в одном и том же положении — обе неподвижны или обе свободны, для образования устойчивых стоячих волн необходимо, чтобы на длине тела укладывалось целое число полуволн.
Если же в теле один конец свободен, а другой закреплен, то для образования упругих стоячих волн необходимо, чтобы на длине его умещалось нечетное число четвертей длин волн.
В работе используется латунный стержень, закрепленный посередине. В месте закрепления находится узел стоячей волны, а на конце — пучности. Если возбудить в нем колебания основного тона , то на длине стержня уложится одна полуволна, а длина волны будет равна его удвоенной длине: .
Источник
Узлы стоячей волны
Стоячие волны
Волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Уравнение стоячей волны
и 
S= 
(учли, что k = 2π/λ)—уравнение стоячей волны.
Пучности стоячей волны
Точки, в которых амплитуда максимальна (Aст = 2Аcos(2πx/λ)) . Это точки среды, для которых
2πx/λ=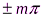 
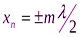
(m=0,1,2,….)
(m = 0,1, 2. ).
Узлы стоячей волны
Точки, в которых амплитуда колебаний равна нулю (Aст = 0). Это точки среды, для которых
(m = 0,1, 2. ).
(m = 0,1, 2. ).
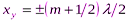
Расстояния пучность—пучность и узел—узел равны λ/2, а расстояние пучность—узел равно λ/4.
Образование стоячих волн наблюдают при
интерференции бегущей и отраженной волн. Например, если конец веревки закрепить неподвижно, то отраженная в месте закрепления веревки волна будет интерферировать с бегущей волной и образует стоячую волну. На границе, где происходит отражение волны, в данном случае получается узел. Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения получается пучность, если более плотная — узел. Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы происходит сложение колебаний противоположных направлений, в результате чего получается узел. Если волна отражается от менее плотной среды, то изменения фазы не происходит, и у границы колебания складываются с одинаковыми фазами — получается пучность.
Уравнение стоячей волны и его анализ
Частным случаем интерференции волн, являются стоячие волны.
Стоячей волной называется волна, образующаяся в результате наложения двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды, а в случае поперечных волн еще и одинаковую поляризацию.
Поперечная стоячая волна образуется, например, на натянутой упругой нити, один конец которой закреплен, а другой приводится в колебательное движение.
При наложении двух когерентных бегущих плоских волн вида
и 
где α-разность фаз волн в точках плоскости x=0, образуется плоская синусоидальная стоячая волна, описываемая уравнением
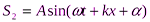
Амплитуда стоячей волны в отличие от амплитуды бегущих волн является периодической функцией координаты x.
Точки ,в которых амплитуда стоячей волны равна 0, называются узлами, а точки где амплитуда двойная –пучности.
Положение узлов и пучностей находится из условий
k*x+α/2=m*n (пучности) ,где m=0,1,2…
Расстояния между двумя соседними узлами и между двумя соседними пучностями одинаковы и равны половине длины волны λ бегущих волн.
В бегущей волне фаза колебаний зависит от координаты x рассматриваемой точки. В стоячей волне все точки между двумя узлами колеблются с различными амплитудами, но с одинаковыми фазами (синфазно), так как аргумент синуса в уравнении стоячей волны не зависит от координаты x. При переходе через узел фаза колебаний изменяется скачком на π,так как при этом cos(k*x+α/2) изменяет свой знак на противоположный.
Источник
Условия возникновения пучностей стоячей волны вывести координаты пучностей
Если в среде распространяется несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Волны накладываются друг на друга, не возмущая (не искажая друг друга). Это и есть принцип суперпозиции волн.
Если две волны, приходящие в какую-либо точку пространства, обладают постоянной разностью фаз, такие волны называются когерентными. При сложении когерентных волн возникает явление интерференции.
Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении от преград.
Напишем уравнения двух плоских волн, распространяющихся в противоположных направлениях (начальная фаза 
):
Сложим уравнения и преобразуем по формуле суммы косинусов (5.4.3):
.
Т.к. 
, то можно записать:
.
Учитывая, что 
, получим уравнение стоячей волны:
В выражении для фазы не входит координата, поэтому можно записать:
где суммарная амплитуда 
.
В точках, где координаты удовлетворяют условию 
(n = 1, 2, 3, …), 
, суммарная амплитуда равна максимальному значению: 
, – это пучности стоячей волны. Координаты пучностей:
 | |
| а | б |
| Рис. 5.5 | |
В точках, координаты которых удовлетворяют условию 
(n = 0, 1, 2,…), 
и суммарная амплитуда колебаний равна нулю 
, – это узлы стоячей волны. Координаты узлов:
Точки среды, находящиеся в узлах, колебаний не совершают.
Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (рис. 5.5, а), и узел – если более плотная (рис. 5.5, б).
Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.
Источник
