Python как вывести первую цифру после точки

Для целых чисел определены операции + , — , * и ** . Операция деления / для целых чисел возвращает вещественное число (значение типа float ). Также функция возведения в степень возвращает значение типа float , если показатель степени — отрицательное число.

Но есть и специальная операция целочисленного деления, выполняющегося с отбрасыванием дробной части, которая обозначается // (она соответствует операции div в Паскале). Она возвращает целое число: целую часть частного. Другая близкая ей операция − это операция взятия остатка от деления, обозначаемая % (она соответствует операции mod в Паскале). Например:

2. Действительные числа

В этом разделе речь пойдет о действительных числах, имеющих тип float .

Обратите внимание, что если вы хотите считать с клавиатуры действительное число, то результат, возращаемый функцией input() необходимо преобразовывать к типу float :

Действительные (вещественные) числа представляются в виде чисел с десятичной точкой (а не запятой, как принято при записи десятичных дробей в русских текстах). Для записи очень больших или очень маленьких по модулю чисел используется так называемая запись «с плавающей точкой» (также называемая «научная» запись). В этом случае число представляется в виде некоторой десятичной дроби, называемой мантиссой, умноженной на целочисленную степень десяти (порядок). Например, расстояние от Земли до Солнца равно 1.496·10 11 , а масса молекулы воды 2.99·10 -23 .

Числа с плавающей точкой в программах на языке Питон, а также при вводе и выводе записываются так: сначала пишется мантисса, затем пишется буква e , затем пишется порядок. Пробелы внутри этой записи не ставятся. Например, указанные выше константы можно записать в виде 1.496e11 и 2.99e-23 . Перед самим числом также может стоять знак минус.

Напомним, что результатом операции деления / всегда является действительное число ( float ), в то время как результатом операции // является целое число ( int ).

Преобразование действительных чисел к целому производится с округлением в сторону нуля, то есть int(1.7) == 1 , int(-1.7) == -1 .

3. Библиотека math

Для проведения вычислений с действительными числами язык Питон содержит много дополнительных функций, собранных в библиотеку (модуль), которая называется math .

Для использования этих функций в начале программы необходимо подключить математическую библиотеку, что делается командой

Например, пусть мы хотим округлять вещественные числа до ближайшего целого числа вверх. Соответствующая функция ceil от одного аргумента вызывается, например, так: math.ceil(x) (то есть явно указывается, что из модуля math используется функция ceil ). Вместо числа x может быть любое число, переменная или выражение. Функция возращает значение, которое можно вывести на экран, присвоить другой переменной или использовать в выражении:

Другой способ использовать функции из библиотеки math , при котором не нужно будет при каждом использовании функции из модуля math указывать название этого модуля, выглядит так:

Ниже приведен список основных функций модуля math . Более подробное описание этих функций можно найти на сайте с документацией языка Питон.

Источник

Работа с числами в Python

В этом материале рассмотрим работу с числами в Python. Установите последнюю версию этого языка программирования и используйте IDE для работы с кодом, например, Visual Studio Code.

В Python достаточно просто работать с числами, ведь сам язык является простым и одновременно мощным. Он поддерживает всего три числовых типа:

int (целые числа)
float (числа с плавающей точкой)
complex (комплексные числа)

Хотя int и float присутствуют в большинстве других языков программирования, наличие типа комплексных чисел — уникальная особенность Python. Теперь рассмотрим в деталях каждый из типов.

Целые и числа с плавающей точкой в Python

В программирование целые числа — это те, что лишены плавающей точкой, например, 1, 10, -1, 0 и так далее. Числа с плавающей точкой — это, например, 1.0, 6.1 и так далее.

Создание int и float чисел

Для создания целого числа нужно присвоить соответствующее значение переменной. Возьмем в качестве примера следующий код:

Здесь мы присваиваем значение 25 переменной var1 . Важно не использовать одинарные или двойные кавычки при создании чисел, поскольку они отвечают за представление строк. Рассмотрим следующий код.

В этих случаях данные представлены как строки, поэтому не могут быть обработаны так, как требуется. Для создания числа с плавающей точкой, типа float , нужно аналогичным образом присвоить значение переменной.

Здесь также не стоит использовать кавычки.

Проверить тип данных переменной можно с помощью встроенной функции type() . Можете проверить результат выполнения, скопировав этот код в свою IDE.

В Python также можно создавать крупные числа, но в таком случае нельзя использовать запятые.

Если попытаться запустить этот код, то интерпретатор Python вернет ошибку. Для разделения значений целого числа используется нижнее подчеркивание. Вот пример корректного объявления.

Значение выведем с помощью функции print :

Арифметические операции над целыми и числами с плавающей точкой

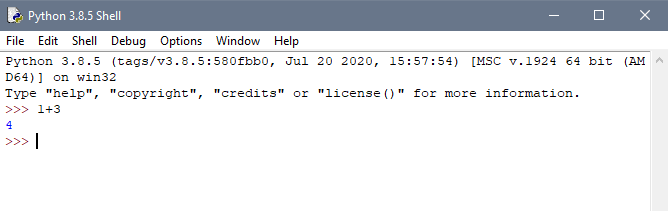
Используем такие арифметические операции, как сложение и вычитание, на числах. Для запуска этого кода откройте оболочку Python, введите python или python3 . Терминал должен выглядеть следующим образом:

Сложение

В Python сложение выполняется с помощью оператора + . В терминале Python выполните следующее.

Результатом будет сумма двух чисел, которая выведется в терминале.

Теперь запустим такой код.

В нем было выполнено сложение целого и числа с плавающей точкой. Можно обратить внимание на то, что результатом также является число с плавающей точкой. Таким образом сложение двух целых чисел дает целое число, но если хотя бы один из операндов является числом с плавающей точкой, то и результат станет такого же типа.

Вычитание

В Python для операции вычитания используется оператор -. Рассмотрим примеры.

Положительные числа получаются в случае вычитания маленького числа из более крупного. Если же из маленького наоборот вычесть большое, то результатом будет отрицательно число. По аналогии с операцией сложения при вычитании если один из операндов является числом с плавающей точкой, то и весь результат будет такого типа.

Умножение

Если перемножить два целых числа, то результатом будет целое число. Если же использовать число с плавающей точкой, то результатом будет также число с плавающей точкой.

Деление

В Python деление выполняется с помощью оператора / .

В отличие от трех предыдущих операций при делении результатом всегда будет число с плавающей точкой. Также нужно помнить о том, что на 0 делить нельзя, иначе Python вернет ошибку ZeroDivisionError . Вот пример такого поведения.

Деление без остатка

При обычном делении с использованием оператора / результатом будет точное число с плавающей точкой. Но иногда достаточно получить лишь целую часть операции. Для этого есть операции интегрального деления. Стоит рассмотреть ее на примере.

Результатом такой операции становится частное. Остаток же можно получить с помощью модуля, о котором речь пойдет дальше.

Остаток от деления

Для получения остатка деления двух чисел используется оператор деления по модулю % .

На этих примерах видно, как это работает.

Возведение в степень

Число можно возвести в степень с помощью оператора ** .

Комплексные числа

Комплексные числа — это числа, которые включают мнимую часть. Python поддерживает их «из коробки». Их можно запросто создавать и использовать. Пример:

Источник

Арифметика с типом float в Python: проблемы и ограничения.

Числа с плавающей точкой представлены в компьютерах в виде двоичных дробей. Например, десятичная дробь 0.125 имеет значение 1/10 + 2/100 + 5/1000 , и таким же образом двоичная дробь 0.001 имеет значение 0/2 + 0/4 + 1/8 . Эти две дроби имеют одинаковые значения, единственное реальное отличие состоит в том, что первая записана в дробной записи с основанием 10, а вторая — с основанием 2.

К сожалению, большинство десятичных дробей не могут быть представлены точно как двоичные дроби. Следствием этого является то, что, как правило, вводимые десятичные числа с плавающей запятой аппроксимируются только двоичными числами с плавающей запятой, фактически сохраненными в машине.

Сначала проблему легче понять из базы 10. Рассмотрим дробь 1/3. Вы можете приблизить это как основную 10 фракцию: 0.3 или лучше, 0.33 или лучше, 0.333 и так далее. Независимо от того, сколько цифр вы хотите записать, результат никогда не будет ровно 1/3 , но будет все более приближенным к 1/3 .

Таким же образом, независимо от того, сколько цифр из 2-х оснований вы хотите использовать, десятичное значение 0,1 не может быть представлено в точности как дробь из 2-х оснований. В базе 2 1/10 — бесконечно повторяющаяся дробь 0.0001100110011001100110011.

Остановитесь на любом конечном количестве битов, и вы получите приближение. На большинстве современных машин числа с плавающей запятой аппроксимируются с использованием двоичной дроби, а числитель использует первые 53 бита, начиная с самого старшего бита, а знаменатель — как степень двух. В случае 1/10 двоичная дробь равна 3602879701896397/2 ** 55 , что близко, но не точно равно истинному значению 1/10 .

Многие пользователи не знают о приближении из-за способа отображения значений. Python печатает только десятичное приближение к истинному десятичному значению двоичного приближения, хранящегося на машине. На большинстве машин, если бы Python должен был печатать истинное десятичное значение двоичного приближения, хранящегося для 0.1, он должен был бы отображать

Это больше цифр, чем большинство людей считают полезным, поэтому Python сохраняет количество цифр управляемым, отображая округленное значение вместо

Просто помните, что хотя напечатанный результат выглядит как точное значение 1/10, фактическое сохраненное значение является ближайшей представимой двоичной дробью.

Интересно, что существует много разных десятичных чисел, которые имеют одну и ту же ближайшую приблизительную двоичную дробь. Например, числа 0.1 и 0.10000000000000001 и 0.1000000000000000055511151231. все приблизительно равны 3602879701896397/2 ** 55 . Поскольку все эти десятичные значения имеют одинаковую аппроксимацию, любое из них может отображаться при сохранении инварианта eval(repr(x)) == x .

Исторически Python и встроенная функция repr() выбирали функцию с 17 значащими цифрами, 0.10000000000000001 . Начиная с Python 3.1 в большинстве систем теперь может выбирать самый короткий из них и просто отображать 0.1.

Обратите внимание, что это по своей природе двоичное число с плавающей точкой: это не ошибка в Python и не ошибка в вашем коде. Вы увидите то же самое на всех языках, которые поддерживают арифметику с плавающей запятой.

Для более приятного вывода вы можете использовать форматирование строки для получения ограниченного числа значащих цифр:

Важно понимать, что в действительности это иллюзия: вы просто округляете отображение истинного значения.

Одна иллюзия может породить другую. Например, поскольку 0,1 не является точно 1/10, суммирование трех значений 0,1 может также не дать точно 0,3:

Кроме того, поскольку 0,1 не может приблизиться к точному значению 1/10, а 0,3 не может приблизиться к точному значению 3/10, предварительное округление функцией round() может не помочь:

Двоичная арифметика с плавающей точкой содержит много сюрпризов, подобных этому. Проблема с 0.1 подробно объясняется в разделе «Ошибка представления». Смотрите также «Опасности с плавающей точкой» для более полного описания других распространенных сюрпризов.

Как говорится, «простых ответов нет». Тем не менее, не следует чрезмерно опасаться чисел с плавающей запятой! Ошибки в операциях с плавающей запятой Python наследуются от аппаратного обеспечения чисел с плавающей запятой, и на большинстве машин они имеют порядок не более одной части в 2 ** 53 на операцию. Это более чем достаточно для большинства задач, но вам нужно помнить, что это не десятичная арифметика и что каждая операция с плавающей запятой может подвергаться новой ошибке округления.

Несмотря на то, что патологические случаи существуют, для наиболее случайного использования арифметики с плавающей запятой вы увидите ожидаемый результат в конце, если просто округлите отображение окончательных результатов до ожидаемого количества десятичных цифр. str() обычно достаточно, и для более точного управления смотрите спецификаторы формата метода str.format() .

Для случаев использования, которые требуют точного десятичного представления, попробуйте использовать модуль decimal , который реализует десятичную арифметику, подходящую для приложений бухгалтерского учета и высокоточных приложений.

Другая форма точной арифметики поддерживается модулем fractions , который реализует арифметику, основанную на рациональных числах, поэтому числа, такие как 1/3 могут быть представлены точно.

Если вы большой пользователь операций с плавающей запятой, вам следует взглянуть на пакет Numeric Python и многие другие пакеты для математических и статистических операций, предоставляемых проектом SciPy .

Python предоставляет инструменты, которые могут помочь в тех редких случаях, когда вы действительно хотите узнать точное значение числа с плавающей точкой. Метод float.as_integer_ratio() выражает значение типа float в виде дроби:

Поскольку отношение является точным, оно может быть использовано для воссоздания исходного значения без потерь:

Метод float.hex() выражает число с плавающей запятой в шестнадцатеричном формате (основание 16), снова давая точное значение, сохраненное компьютером:

Это точное шестнадцатеричное представление может быть использовано для точного восстановления значения с плавающей точкой:

Поскольку представление является точным, оно полезно для надежного переноса значений между различными версиями Python и обмена данными с другими языками, поддерживающими тот же формат, например Java.

Другим полезным инструментом является функция math.fsum() , которая помогает уменьшить потерю точности во время суммирования. Она отслеживает «потерянные цифры», когда значения добавляются в промежуточный итог. Это может повлиять на общую точность, так что ошибки не накапливаются до такой степени, что бы влиять на итоговую сумму:

Ошибка представления.

В этом разделе подробно объясняется пример 0.1 и показано, как вы можете выполнить точный анализ подобных случаев самостоятельно. Предполагается базовое знакомство с двоичным представлением чисел с плавающей точкой.

Ошибка представления относится к тому факту, что фактически большинство десятичных дробей не могут быть представлены точно как двоичные дроби (основание 2) . Это главная причина, почему Python или Perl, C, C++, Java, Fortran и многие другие языки часто не будут отображать точное десятичное число, которое ожидаете.

Это почему? 1/10 не совсем представимо в виде двоичной дроби. Почти все машины сегодня используют арифметику IEEE-754 с плавающей точкой, и почти все платформы отображают плавающие значения Python в IEEE-754 с «двойной точностью». При вводе, компьютер стремится преобразовать 0,1 в ближайшую дробь по форме J / 2 ** N , где J — целое число, содержащее ровно 53 бита.

Перепишем 1 / 10

= 2**N / 10 и напоминая, что J имеет ровно 53 бита, это >= 2**52 , но , наилучшее значение для N равно 56:

То есть 56 — единственное значение для N , которое оставляет J точно с 53 битами. Наилучшее возможное значение для J тогда будет округлено:

Поскольку остаток больше половины от 10, наилучшее приближение получается округлением вверх:

Поэтому наилучшее возможное приближение к 1/10 при двойной точности 754: 7205759403792794 / 2 ** 56 . Деление числителя и знаменателя на два уменьшает дробь до: 3602879701896397 / 2 ** 55

Обратите внимание, поскольку мы округлили вверх, то значение на самом деле немного больше, чем 1/10 . Если бы мы не округлили, то значение был бы немного меньше 1/10 . Но ни в коем случае это не может быть ровно 1/10 !

Таким образом, компьютер никогда не «видит» 1/10: то, что он видит, это точная дробь, указанная выше, наилучшее двоичное приближение 754, которое он может получить:

Если мы умножим эту дробь на 10 ** 55 , мы увидим значение до 55 десятичных цифр:

Это означает, что точное число, хранящееся в компьютере, равно десятичному значению полученному выше. Вместо отображения полного десятичного значения многие языки, включая более старые версии Python округляют результат до 17 значащих цифр:

Модули fractions and decimal упрощают эти вычисления:

Источник

Python как вывести первую цифру после точки

Вывод числа после точки

Решение

Решение