Почему ср больше чем сv выведите уравнение майера

Теплоёмкость газа, cV и cP, соотношение Майера.

Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.

Молярная теплоемкость C:

M – молярная масса вещества

Все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов:

C_V – молярная теплоемкость в изохорном процессе (V = const) и

C_p – молярная теплоемкость в изобарном процессе (p = const).

В процессе при V= const A = 0. Из 1 закона термодинамики для 1 моля газа:

QV = CV ΔT = ΔU

Для процесса при p=const 1 закон термодинамики:

Qp = ΔU + p (V2 – V1) = CV ΔT + pΔV

, где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT.

Соотношение, выражающее связь между молярными теплоемкостями C_p и C_V, имеет вид (формула Майера):

Cp = CV + R.

Два возможных процесса нагревания газа на ΔT = T₂ – T₁. При p = const газ совершает работу A = p₁(V₂ – V₁). Поэтому C_p > C_V
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом:

, при p=const
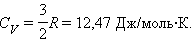
Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна

Из этой теоремы следует, что молярные теплоемкости газа C_p и C_V и их отношение γ могут быть записаны в виде

где i – число степеней свободы газа.

Для газа, состоящего из одноатомных молекул (i = 3)

Для газа, состоящего из двухатомных молекул (i = 5)

Для газа, состоящего из многоатомных молекул (i = 6)

Источник

Уравнение Майера

Уравнение Майера связывает теплоемкости идеального газа в двух изопроцессах, тогда перейдем к самому его определению.

Теплоемкость. Уравнение Майера

Переданное телу количество теплоты для его нагревания на 1 К получило название теплоемкости тела данной системы. Обозначение принимается буквой » С » :

Значение теплоемкости единицы молярной массы тела:

c μ = C v ( 2 ) . Выражение называется молярной теплоемкостью.

Теплоемкость не считается функцией состояния, так как является характеристикой бесконечно близких состояний системы или выражается в качестве функции бесконечно малого процесса, совершаемого в системе. В количественном выражении это означает, что из ( 1 ) , применяя первое начало термодинамики, дифференциальная форма получится:

C = δ Q d T = d U + p d V d T ( 3 ) .

Уравнение Майера для идеального газа

Определение термодинамической системы производится при помощи трех параметров p , V , T . Существующее между ними отношение получило название уравнения состояния. Для идеального газа используется уравнение Менделеева-Клапейрона. Данная связь запишется в виде:

p = p ( T , V ) или T = T ( p , V ) , V = V ( p , T ) .

При выборе независимых переменных в качестве V и T внутренняя энергия системы выражается в виде функции U = U ( T , V ) . Получим, что значение полного дифференциала от внутренней энергии примет вид:

d U = ∂ U ∂ T V d T + ∂ U ∂ V T d V ( 4 ) .

Произведем подстановку из ( 4 ) в ( 3 ) , тогда

c = ∂ U ∂ T V d T + ∂ U ∂ V T d V + p d V d T = ∂ U ∂ T V + p + ∂ U ∂ V T d V d T ( 5 ) .

Исходя из формулы ( 5 ) , теплоемкость находится в зависимости от процесса. Если он изохорный, то

Значение теплоемкости изохорного процесса запишется как:

C V = ∂ U ∂ T V ( 6 ) .

При изобарном теплоемкость выражается через формулу:

C p = ∂ U ∂ T V + p + ∂ U ∂ V T ∂ V ∂ T p = C V + p + ∂ U ∂ V T ∂ V ∂ T p ( 7 ) .

Перейдем к рассмотрению исследуемой системе идеального газа. Запись малого приращения энергии идеального газа:

d U = i 2 v R d T ( 8 ) .

d U d V T = 0 ( 9 ) .

Состояние идеального газа описывается при помощи уравнения Менделеева-Клапейрона:

∂ V ∂ T p = v R p ( 11 ) .

Произведем подстановку в ( 7 ) из ( 10 ) и ( 11 ) :

C p = C V + p + 0 v R p = C V + v R ( 12 ) .

Выражение ( 12 ) называют выведенным соотношением Майера.

Или для молярных теплоемкостей:

C μ p = C μ V + R ( 13 ) .

Найти удельную теплоемкость смеси 16 г кислорода и 10 г гелия в процессе с постоянным давлением.

Если Q считается количеством тепла, получаемым смесью газов в процессе, то

Q = c p m ∆ T ( 1 . 1 ) , где m является массой смеси, c p – удельной теплоемкостью смеси при неизменном давлении.

Q O 2 — это количество тепла, получаемое кислородом:

Q O 2 = c p O 2 m O 2 ∆ T ( 1 . 2 ) , m O 2 выражается массой кислорода, c p O 2 – теплоемкостью кислорода с постоянным давлением.

Для гелия аналогично:

Q H e = c p H e m H e ∆ T ( 1 . 3 ) .

Кроме этого рассмотрим:

Q = c p m ∆ T = Q O 2 + Q H e = c p O 2 m O 2 ∆ T + c p H e m H e ∆ T ( 1 . 4 ) .

Нахождение массы смеси производится по закону сохранения массы:

m = m O 2 + m H e ( 1 . 5 ) .

Произведем выражение теплоемкости c p из ( 1 . 4 ) , учитывая ( 1 . 5 ) . Тогда имеем:

c p = c p O 2 m O 2 + c p H e m H e m O 2 + m H e ( 1 . 6 ) .

Существует связь между молярной теплоемкостью и удельной:

c μ = c · μ → c = c μ μ ( 1 . 7 ) .

Если c μ V = i 2 R , то по уравнению Роберта Майера c μ p = c μ V + R :

c μ p = i + 2 2 R ( 1 . 8 ) ; i H e = 3 , i O 2 = 5 .

В данном случае удельные теплоемкости запишутся как:

c p H e = 5 2 R μ H e , c p O 2 = 7 R 2 μ O 2 ( 1 . 9 ) .

Результатом будет записанная формула удельной теплоемкости смеси:

c p = 7 R 2 μ O 2 m O 2 + 5 2 R μ H e m H e m O 2 + m H e ( 1 . 10 ) .

c p = 3 , 5 · 8 , 31 · 16 32 + 2 , 5 · 8 , 31 · 10 4 26 = 14 , 5 + 51 , 94 26 = 2 , 56 Д ж г К .

Ответ: удельная теплоемкость смеси равняется 2 , 56 Д ж г К .

При проведении опытов Джоулем было получено, что с μ p — c μ V = 1 , 986 к а л К · м о л ь . Значение газовой постоянной, измеренной в механических единицах R = 8 , 314 · 10 7 э р г К · м о л ь . Определите, как соотносятся 1 к а л , э р г , Д ж .

Основой решения данного задания принято считать уравнение Майера, формула записывается:

с μ p = c μ V + R → c μ p — c μ V = R ( 2 . 1 ) .

Отсюда получим, что:

c μ p — c μ V = 1 , 986 к а л К · м о л ь = 8 , 314 · 10 7 э р г К · м о л ь → 1 к а л = 4 , 18 · 10 7 э р г = 4 , 18 Д ж .

Ответ: 1 к а л = 4 , 18 · 10 7 э р г = 4 , 18 Д ж .

Источник

Почему ср больше чем сv. Теплоёмкость идеального газа

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

2. Что такое степени свободы молекул? Как число степеней свободы связано с коэффициентом Пуассона γ?

Числом степеней свободы тела называется число независимых координат, которые необходимо задать для того, чтобы полностью определить положение тела в пространстве. Так, например, материальная точка, произвольно движущаяся в пространстве, обладает тремя степенями свободы (координаты x, y, z).

Молекулы одноатомного газа можно рассматривать как материальные точки на том основании, что масса такой частицы (атома) сосредоточена в ядре, размеры которого очень малы (10 -13 см). Поэтому молекула одноатомного газа может иметь лишь три степени свободы поступательного движения.

Молекулы, состоящие из двух, трех и большего числа атомов, не могут быть уподоблены материальным точкам. Молекула двухатомного газа в первом приближении представляет собой два жестко связанных атома, находящихся на некотором расстоянии друг от друга

3. Чему равна теплоемкость идеального газа при адиабатическом процессе?

Теплоемкостью называется величина, равная количеству теплоты, которое нужно сообщить веществу, чтобы повысить его температуру на один кельвин.

4. В каких единицах измеряются в системе си давление, объем, температура, молярные теплоемкости?

Давление – кПа, объем – дм 3 , температура – в Кельвинах, молярные теплоемкости – Дж/(мольК)

5. Что такое молярные теплоемкости Ср и Сv?

У газа различают теплоемкость при постоянном объеме С v и теплоемкость при постоянном давлении С р.

При постоянном объеме работа внешних сил равна нулю, и все сообщаемое газу извне количество теплоты идет целиком на увеличение его внутренней энергии U. Отсюда молярная теплоемкость газа при постоянном объеме С v численно равна изменению внутренней энергии одного моля газа ∆Uпри повышении его температуры на 1К:

Таким образом, молярная теплоемкость газа при постоянном объеме

удельная теплоемкость при постоянном объеме

При нагревании газа при постоянном давлении газ расширяется, сообщаемое ему извне количество теплоты идет не только на увеличение его внутренней энергии U, но и на совершение работыAпротив внешних сил. Следовательно, теплоемкость газа при постоянном давлении больше теплоемкости при постоянном объеме на величину работыA, которую совершает один моль газа при расширении, происходящем в результате повышения его температуры на 1Kпри постоянном давленииP:

Можно показать, что для моля газа работа A=R, тогда

Пользуясь соотношением между удельными в молярными теплоемкостями, находим для удельной теплоемкости:

Непосредственное измерение удельных и молярных теплоемкостей затруднительно, так как теплоемкость газа составит ничтожную долю теплоемкости сосуда, в котором находится газ, и поэтому измерение будет чрезвычайно неточно.

Проще измерить отношение величии С р / С v

Это отношение зависит только от числа степеней свободы молекул, из которых состоит газ.

Где А – атомная масса; m ед — атомная единица массы; N А — число Авогадро; моль μ – количество вещества, в котором содержится число молекул, равное числу атомов в 12 г изотопа углерода 12 С.

Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.

Если газ нагревать при постоянном объёме , то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается С V .

С Р – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h , то есть газ совершит работу (рис. 4.2).

Рис. 4.2

Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что .

Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния.

Величины С Р и С V оказываются связанными простыми соотношениями. Найдём их.

Пусть мы нагреваем один моль идеального газа при постоянном объёме(dA = 0). Тогда первое начало термодинамики запишем в виде:

Т.е. бесконечно малое приращение количества теплоты равно приращению внутренней энергии dU .

Теплоемкость при постоянном объёме будет равна:

Так как U может зависеть не только от температуры. Но в случае идеального газа справедлива формула (4.2.4).

Из (4.2.4) следует, что

,

При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:

Удельная теплоемкость вещества — величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:

Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кг К)).

Молярная теплоемкость — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:

где ν =m/М-количество вещества.

Единица молярной теплоемкости — джоуль на моль кельвин (Дж/(моль К)).

Удельная теплоемкость с связана с молярной теплоемкостью С m , соотношение

где М — молярная масса вещества.

Выделяют теплоемкости при постоянном объеме и постоянном давлении, если в процессе нагревания вещества его объем или давление поддерживается постоянным. Запишем выражение первого начала термодинамики для одного моль газа с учетом (1) и δA=pdV

Если газ нагревается при постоянном объеме, то dV=0 и работа внешних сил равна также равна нулю. Тогда газу сообщаемая извне теплота идет только на увеличение его внутренней энергии:

(4) т. е. молярная теплоемкость газа при постоянном объеме С V равна изменению внутренней энергии одного моль газа при повышении его температуры на 1 К. Поскольку U m =(i /2)RT ,

Если газ нагревается при постоянном давлении, то выражение (3) можно представить в виде

Учитывая, что (U m /dT) не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна С V , и дифференцируя уравнение Клапейрона — Менделеева pV m =RT по T (p=const), получаем

Выражение (6) называется уравнением Майера; оно говорит о том, что С p всегда больше С V ровно на величину молярной газовой постоянной. Это объясняется тем, чтобы осуществить нагревание газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Использовав (5), формулу (6) можно записать в виде

При исследовании термодинамических процессов важно знать характерное для каждого газа отношение С p к С V:

(8)

называется показателем адиабаты . Из молекулярно-кинетической теории идеальных газов известны численные значения показателя адиабаты, они зависят от числа атомов в молекуле газа:

Одноатомный газ γ = 1,67;

Двухатомный газ γ = 1,4;

Трех- и многоатомный газ γ = 1,33.

(Еще показатель адиабаты обозначается k)

11. Теплота. Первое начало термодинамики.

Внутренняя энергия термодинамической системы может изменяться двумя способами: посредством совершения работы над системой и посредством теплообмена с окружающей средой. Энергия, которую получает или теряет тело в процессе теплообмена с окружающей средой, называется коли́чеством теплоты́ или просто теплотой .

Единица измерения в (СИ) — джоуль. Как единица измерения теплоты используется также калория.

Первое начало термодинамики — одно из основных положений термодинамики, являющееся, по существу, законом сохранения энергии в применении к термодинамическим процессам.

Первое начало термодинамики было сформулировано в середине XIX века в результате работ Ю. Р. Майера, Джоуля и Г. Гельмгольца. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя 1-го рода, который совершал бы работу, не черпая энергию из какого-либо источника.

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы против внешних сил.

Первый закон термодинамики можно сформулировать так:

«Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты Q, сообщенного системе, в сумме с изменением энергии, связанной с количеством вещества N при химическом потенциале , и работы A», совершённой над системой внешними силами и полями, за вычетом работы А, совершённой самой системой против внешних сил»:

Для элементарного количества теплоты , элементарной работыи малого приращения (полного дифференциала)внутренней энергии первый закон термодинамики имеет вид:

Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая – работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.

Важно заметить, что иявляются полнымидифференциалами, а и- нет. Приращение теплоты часто выражают через температуру и приращениеэнтропии: .

Цель работы : Изучение тепловых процессов в идеальном газе, ознакомление с методом Клемана-Дезорма и экспериментальное определение отношения молярных теплоемкостей воздуха при постоянном давлении и постоянном объеме.

Описание установки и метода изучения процесса

Внешний вид рабочей панели и принципиальная схема экспериментальной установки ФПТ1-6н представлена на рис. 8: 1 – включатель «СЕТЬ» для питания установки; 2 – включатель «Компрессор» для нагнетания воздуха в рабочий сосуд (емкость объемом V = 3500 см 3), расположенный в полости корпуса; 3 – кран К1, необходимый для предотвращения сброса давления из рабочего сосуда после остановки компрессора; 4 – пневмотумблер «Атмосфера», позволяющий на короткое время соединять рабочий сосуд с атмосферой; 5 – измеритель давления с помощью датчика давления в рабочем сосуде;

Рис. 8. Внешний вид рабочей панели

6 – двухканальный измеритель температуры, позволяющий измерить температуру внутри окружающей среды и температуру внутри рабочего сосуда.

Состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р , объемом V и температурой Т . Уравнение, устанавливающее связь между этими параметрами, называется уравнением состояния. Для идеальных газов таким уравнением является уравнение Клапейрона-Менделеева:

где m – масса газа; μ – молярная масса; R = 8,31 Дж/моль∙К – универсальная газовая постоянная.

Любое изменение состояния термодинамической системы, связанное с уменьшением или увеличением хотя бы одного из параметров р, V, Т, называется термодинамическим процессом.

Изопроцессы – это процессы, протекающие при одном постоянном параметре:

изобарический – при р = const ;

изохорический – при V = const ;

изотермический – при Т = const .

Адиабатический процесс совершается без теплообмена с окружающей средой, поэтому для его осуществления систему теплоизолируют или ведут процесс так быстро, чтобы теплообмен не успел произойти. При адиабатическом процессе изменяются все три параметра р , V , Т .

При адиабатическом сжатии идеального газа температура его повышается, а при расширении понижается. На рис. 9 в системе координат р и V изображены изотерма (рV = const ) и адиабата (рV γ = const ). Из рисунка видно, что адиабата проходит круче изотермы. Объясняется это тем, что при адиабатическом сжатии увеличение давления газа происходит не только из-за уменьшения его объема, как при изотермическом сжатии, но и за счет повышения температуры.

Рис. 9. рV = const; рV γ = const

Теплоемкостью вещества (тела) называется величина, равная количеству теплоты, необходимому для нагревания его на один Кельвин. Она зависит от массы тела, его химического состава и вида процесса теплоты. Теплоемкость одного моля вещества называется молярной теплоемкостью С μ .

Согласно первому началу термодинамики количество теплоты dQ , сообщенное системе, расходуется на увеличение внутренней энергии dU системы и совершение системой работы dA против внешних сил

Используя первое начало термодинамики (2) и уравнение Клапейрона-Менделеева (1), можно вывести уравнение, описывающее адиабатический процесс, – уравнение Пуассона

или в других параметрах:

T γ p 1-γ = const.

В этих уравнениях — показатель адиабаты

где С v и С p – молярные теплоемкости при постоянном объеме и давлении соответственно.

Для идеального газа расчет теплоемкостей С р и С v можно провести теоретически. При нагревании газа при постоянном объеме (изохорический процесс) работа газа dA = рdV равна нулю, поэтому молярная теплоемкость

, (3)

где i – число степеней свободы – количество независимых координат, с помощью которых однозначно можно задать положение молекулы; индекс V означает изохорический процесс.

При изобарном нагревании (p = const ) количество теплоты, подведенное к газу, расходуется на увеличение внутренней энергии и на совершение работы расширения газа:

.

Теплоемкость моля газа при этом равна

Уравнение (5) называется уравнением Майера. Следовательно, разность молярных теплоемкостей С р – С v = R численно равна работе расширения одного моля идеального газа при нагревании его на один Кельвин при постоянном давлении. В этом заключается физический смысл универсальной газовой постоянной R.

Для идеальных газов отношение γ = С р / С v = (i + 2) / i зависит только от числа степеней свободы молекул газа, которое, в свою очередь, определяется структурой молекулы, т.е. количеством атомов, из которых состоит молекула. Одноатомная молекула имеет 3 степени свободы (инертные газы). Если молекула состоит из двух атомов, то число степеней свободы складывается из числа степеней свободы поступательного движения (i пост = 3) центра масс и вращательного (i вр = 2) движения системы вокруг двух осей, перпендикулярных к оси молекулы, т.е. равно 5. Для трех- и многоатомных молекул i = 6 (три поступательные и три вращательные степени свободы).

В данной работе коэффициент γ для воздуха определяется опытным путем.

Если при помощи насоса в сосуд накачать некоторое количество воздуха, то давление и температура воздуха внутри сосуда повысятся. Вследствие теплообмена воздуха с окружающей средой через некоторое время температура воздуха, находящегося в сосуде, сравняется с температурой T 0 внешней среды.

Давление, установившееся в сосуде, равно р 1 = р 0 + р′ , где р 0 – атмосферное давление, р′ – добавочное давление. Таким образом, воздух внутри сосуда характеризуется параметрами (р 0 + р′ ), V 0 , Т 0 , а уравнение состояния имеет вид

. (6)

Если на короткое время (

3с) открыть тумблер «АТМОСФЕРА», то воздух в сосуде будет расширяться. Этот процесс расширения можно рассматривать как подключение к сосуду дополнительного объема V′ . Давление в сосуде станет равным атмосферному Р 0 , температура понизится до Т 1 , а объем будет равен V 0 + V′ . Следовательно, в конце процесса уравнение состояния будет иметь вид

. (7)

Разделив выражение (7) на выражение (6), получим

. (8)

Расширение происходит без теплообмена с внешней средой, т.е. процесс является адиабатическим, поэтому для начального и конечного состояний системы справедливо соотношение

. (9)

Источник