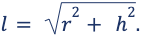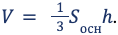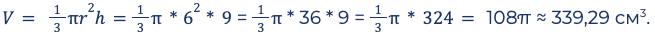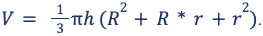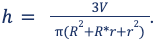Объясните какое тело называется усеченным конусом выведите формулу площади полной поверхности конуса

Усеченный конус: формула объема, площади поверхностей и другое

Содержание:

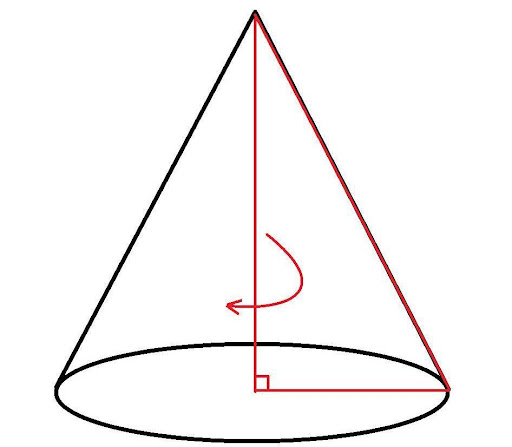
Конус – объемное тело, получаемое посредством вращения треугольника с углом 90° вокруг катета – его высоты. Расстояние от вершины до любой точки круга в основании тела называется образующей. Рассмотрим, как проводится расчет прямого и усеченного конусов: по каким формулам определяют их площади, объемы.

Понятие

Второй вариант образования рассматриваемого геометрического тела: прямоугольный треугольник вращается вокруг катета по или против часовой стрелки. Катет, ставший осью, будет высотой конуса, лежащий в основании – диаметром нижней поверхности, гипотенуза – образующей.

Длина образующих одинакова, их совокупность называется боковой поверхностью. Квадрат длины образующей равняется сумме квадратов высоты и радиуса основания (из теоремы Пифагора): l 2 = h 2 + r 2 . Отсюда

Разновидности конусов

Площадь

Площадь прямого конуса определяется по формуле:

• основания – S_осн = πr 2 ; r – радиус;
• боковой поверхности – S_бп = πrl; l – длина;
• полная – S = S_осн + S_бп = πr 2 + πrl = πr (r + l).

• диаметр равен 12 см;
• длина образующей – 10 см.

Радиус – это половина диаметра: 12/2 = 6 см.

Подставим значения в выражение: S = πr (r + l).

Получим: S = π * 6 *(6 + 10) = 96 π ≈ 301,584 см2.

Как вычислить площадь усеченного конуса

Формула площади полной поверхности усеченного конуса:

S₁ и S₂ – площади поверхностей усеченного конуса.

Подставляем значения и упрощаем:

S = π(r 2 + (r + R)l + R 2 .

Зная радиусы – 6 и 10 см, расстояние от вершины к лежащей на круге точке – 12 см найдём площадь граней.

S = π * (6 2 + (6 + 10) * 12 + 10 2 ) = 328π ≈ 1030,4 см 3 .

Объем усечённого конуса

Объем – пространство, занимаемое геометрическим телом. Численное значение указывает на количество кубиков с гранью единица, помещающихся в конусе. Объем тела вычисляется как треть произведения площади основания на его высоту.

Основание – круг, его поверхность рассчитывается по формуле: S_осн = πr 2 . После подстановки получим:

.

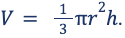
Пример: вычислить объем тела: r = 6 см, h = 9 см. Ставим значения в формулу, пошагово упрощаем выражение.

Если известен диаметр, разделите его на два: .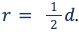

Вычислим объем усеченного конуса. Для понимания, от полного объема исходного тела нужно отнять значение отрезанного параллельной нижней грани плоскостью.

Формула объема усеченного конуса:

Высота

Существует несколько способов как найти высоту усеченного конуса. Какой подойдёт, зависит от исходных данных.

Когда даны радиусы оснований и объем, достаточно провести вычисления:

Для прямого при известном радиусе или диаметре оснований с образующей можно воспользоваться теоремой Пифагора:

Источник

Зачет по теме «Цилиндр, конус, шар»

Карточки для зачета по геометрии в 11 классе

Содержимое разработки

Зачет11_02 по теме:«Цилиндр, конус и шар».

Объясните, какое тело называется цилиндром. Выведите формулу площади полной поверхности цилиндра.

Высота конуса равна 6 см., а образующая наклонена к плоскости основания под углом в 30 о . Найдите площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60 о .

Радиус шара равен R. Найдите площадь поверхности вписанного в шар куба.

Зачет11_02 по теме:«Цилиндр, конус и шар».

Объясните, какое тело называется конусом. Выведите формулу площади полной поверхности конуса.

Радиус шара равен 8 см. Через конец радиуса, лежащего на сфере, проведена плоскость под углом 45 о к радиусу. Найдите площадь сечения шара этой плоскостью.

Куб с ребром а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.

Зачет11_02 по теме:«Цилиндр, конус и шар».

Объясните, какое тело называется усеченным конусом. Выведите формулу площади полной поверхности усеченного конуса.

Сечение цилиндра плоскостью, параллельной оси, отсекает от окружности основания дугу в 90 о . Найдите площадь сечения, если высота цилиндра равна 6 см., а расстояние между осью цилиндра и секущей плоскостью равна 3 см.

Около шара радиуса R описан правильный тетраэдр. Найдите площадь поверхности тетраэдра.

Зачет11_02 по теме:«Цилиндр, конус и шар».

Объясните, какая поверхность называется сферой и какое тело называется шаром. Выведите уравнение сферы в заданной прямоугольной системе координат.

Радиус кругового сектора равен 6 см., а его угол равен 120 о . Сектор свернут в коническую поверхность. Найдите площадь полной поверхности конуса.

Осевое сечение конуса – равносторонний треугольник. В конус вписана треугольная пирамида, основанием которой служит прямоугольный треугольник с катетами 12 см и 16 см. Найдите высоту пирамиды.

Зачет11_02 по теме:«Цилиндр, конус и шар».

Перечислите возможные случаи взаимного расположения сферы и плоскости. Докажите, что сечение сферы плоскостью есть окружность.

Осевое сечение цилиндра – квадрат, диагональ которого равна 12 см. Найдите площадь боковой поверхности цилиндра.

В сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60 о . Найдите площадь сферы.

Зачет11_02 по теме:«Цилиндр, конус и шар».

Сформулируйте определение касательной плоскости к сфере. Докажите теоремы о касательной плоскости (свойство и признак касательной плоскости).

Площадь сечения шара плоскостью, проходящей через его центр, равна 16 см 2 . Найдите площадь сферы.

Диагональ правильной четырехугольной призмы равна 4 см и наклонена к плоскости основания под углом 45 о . Найдите площадь боковой поверхности цилиндра, вписанного в эту призму.

Источник

зачёт по геометрии,помогите пожалуйста.

Карточка 2.
1. Объясните, какое тело называется конусом. Выведите формулу площади полной поверхности конуса.
2. Радиус шара равен 8 см. Через конец радиуса, лежащего на сфере, проведена плоскость под углом 45о к радиусу. Найдите площадь сечения шара этой плоскостью.
3. Куб с ребром а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.

Карточка 3.
1. Объясните, какое тело называется усеченным конусом. Выведите формулу площади полной поверхности усеченного конуса.
2. Сечение цилиндра плоскостью, параллельной оси, отсекает от окружности основания дугу в 90о. Найдите площадь сечения, если высота цилиндра равна 6 см., а расстояние между осью цилиндра и секущей плоскостью равна 3 см.
3. Около шара радиуса R описан правильный тетраэдр. Найдите площадь поверхности тетраэдра.

Карточка 4.
1. Объясните, какая поверхность называется сферой и какое тело называется шаром. Выведите уравнение сферы в заданной прямоугольной системе координат.
2. Радиус кругового сектора равен 6 см., а его угол равен 120о. Сектор свернут в коническую поверхность. Найдите площадь полной поверхности конуса.
Осевое сечение конуса – равносторонний треугольник. В конус вписана треугольная пирамида, основанием которой служит прямоугольный треугольник с катетами 12 см и 16 см. Найдите высоту пирамиды.

Карточка 5.
1. Перечислите возможные случаи взаимного расположения сферы и плоскости. Докажите,что сечение сферы плоскостью есть окружность.
2. Осевое сечение цилиндра-квадрат,диагональ которого равна 12 см. Найдите площадь боковой поверхности цилиндра.
3. В сферу вписан конус,образующая которого равна l, а угол при вершине осевого сечения 60градусов . Найдите площадь сферы.

Набирайте по очереди в поисковике тему — конус, еусеченный конус и так далее. Можете в Википедии почитать, или на математическом сайте.

Ну, а на такое количество вопросов в одном ответе вряд ли кто отвечать будет. Это полдня просидеть, чтобы одной тебе ответить.

Источник

Нахождение площади поверхности усеченного конуса: формулы

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого усеченного кругового конуса (боковую, полную и основания), а также разберем пример решения задачи для закрепления представленного теоретического материала.

Формулы вычисления площади усеченного конуса

Примечание: иногда усеченный конус, также, называют коническим слоем.

1. Боковая поверхность

Чтобы найти площадь (S) боковой поверхности прямого усеченного кругового конуса, необходимо знать длину его образующей, а также радиусы двух оснований.

Примечание: в этой и других формулах ниже число π чаще всего округляется до 3,14.

2. Основания

Основаниями кругового усеченного конуса являются два круга, площади которых считаются таким образом:

Примечание: если вместо радиусов (R или r) даны соответсвующие им диаметры (d), их следует разделить на 2, чтобы получить нужные радиусы.

3. Полная площадь

Чтобы вычислить площадь полной поверхности усеченного конуса, требуется сложить площади его боковой поверхности и двух оснований.

S_полн. = πl(R + r) + πR 2 + πr 2 = π(lR + lr + R 2 + r 2 )

Пример задачи

Найдите площадь поверхности усеченного конуса, если известно, что радиусы его оснований равны 6 и 11 см, а длина образующей составляет 8 см.

Решение

Все известные значения для вычисления площади нам известны, так что остается лишь подставить их в формулы, приведенные выше.

S_бок. = 3,14 ⋅ 8 см ⋅ (6 см + 11 см) = 427,04 см 2

S_осн.1 = 3,14 ⋅ (11 см) 2 = 379,94 см 2

S_осн.2 = 3,14 ⋅ (6 см) 2 = 113,04 см 2

S_полн. = 427,04 см 2 + 379,94 см 2 + 113,04 см 2 =

Источник

Что такое усеченный конус: определение, основные элементы

В данной публикации мы рассмотрим определение и основные элементы усеченного конуса. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение усеченного конуса

Усеченный конус (конический слой) – это геометрическая фигура в пространстве; часть конуса, оставшаяся между его основанием и секущей плоскостью, параллельной этому основанию.

Примечание: В рамках данной публикации мы будем рассматривать самый распространенный вид усеченного конуса – прямой круговой.

Усеченный конус образуется путем вращения на 360° прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию, или равнобедренной трапеции вокруг своей оси симметрии на 180°.

На рисунке ниже конус образован путем вращения равнобедренной трапеции ABCD вокруг оси O₁O₂.

Основные элементы усеченного конуса

• R – радиус бОльшего основания конуса, являющегося кругом, с центром в точке O₁ и диаметром AD.
• r – радиус меньшего основания конуса с центром в точке O₂, диаметр – отрезок BC.
• h (O₁O₂) – высота конуса; одновременно является высотой трапеции ABCD и осью симметрии обеих фигур.

Развёртка боковой поверхности усеченного конуса выглядит следующим образом:

Длина бОльшей (меньшей) дуги равна длине окружности соответствующего основания конуса ( 2πR или 2πr ).

Источник