Как вывести уравнение ван дер ваальса

Уравнение Ван-дер-Ваальса

При низких давлениях и высоких температурах закон Менделеева-Клапейрона также довольно точно описывает поведение реальных газов, однако в других условиях реальные газы значительно отклоняются от идеальности. Уравнение Ван-дер-Ваальса учитывает эти отклонения.

Формула уравнения Ван-дер-Ваальса

Уравнение Ван-дер-Ваальса имеет вид:

В этом уравнении n – количество молей газа, р – его давление, V – занимаемый газом объем, Т – абсолютна температура газа. Универсальная газовая постоянная имеет значение 8,31441 Дж/(моль•К), одинаковое для всех газов.

Переменная а – это поправка на силу притяжения между молекулами газа. Под действием этой силы молекулы притягиваются друг к другу, внутрь газа, уменьшая давление на стенку. Переменная b – поправка, учитывающая собственный объем, занимаемый молекулами газа. Эти поправки зависят от вида газа, и могут быть найдены из таблиц либо рассчитаны по следующим формулам:

Здесь и – это давление и абсолютная температура газа в критической точке, то есть в точке перехода газообразной фазы в жидкую.

В реальном газе расстояния между молекулами меньше, чем в идеальном, и сравнимы с размерами самих молекул. Поэтому силы взаимодействия между молекулами становятся достаточно большими. В объеме газа молекула со всех сторон окружена другими молекулами, и силы их притяжения уравновешиваются. Однако когда молекула приближается к стенке, силы притяжения больше не уравновешиваются и «втягивают» её внутрь. Поэтому молекула движется к стенке медленнее, из-за чего давление на стенку уменьшается. Это и учитывает поправка а.

Кроме того, за счёт сил межмолекулярного взаимодействия реальные газы способны переходить в жидкое состояние, и уравнение Ван-дер-Ваальса довольно точно описывает поведение газов вблизи этого перехода.

Так как в реальном газе расстояние между молекулами сравнительно невелико, молекула должна пролететь меньшее расстояние, чтобы удариться о стенку. Поэтому при очень больших давлениях давление на стенку возрастает, и это учитывает поправка b.

Уравнение Ван-дер-Ваальса применяется, в частности, при определении параметров пара в теплотехнике и теплотехнике, при исследовании сжижения газов.

Примеры решения задач

Задание	Какую температуру имеет азот массой 2 грамма, занимающий объём 800 см при давлении 0,2 МПа, если его рассматривать как реальный газ?
Решение	Для удобства переведем значения величин в систему СИ:

800 см 3 = 0,0008 м 3 ;

0,2 МПа = 2•10 5 Па.

Табличные значения поправок a и b для азота:

a = 0,136 Па•м 6 /моль 2 ;

b = 3,85•10 -5 м 3 /моль.

Определим, сколько молей содержится в 4 г водорода. Учтём, что водород – двухатомный газ, поэтому его молекулярная масса М – сумма двух атомных масс водорода А.

=0,071 моль.

Выразим температуру из уравнения Ван-дер-Ваальса:

Ответ

Задание

Вычислить поправки a и b в уравнении Ван-дер-Ваальса для азота, если известны критическая температура Ткр = 126 К и критическое давление ркр = 3,39 МПа.

Решение Помножив уравнение Ван-дер-Ваальса на и разделив на p, получим кубическое уравнение относительно объема:

Это уравнение имеет три корня. В точке перегиба, показанной на рисунке, все эти корни действительны и равны друг другу. Точка перегиба и есть критической точкой, в которой газообразная фаза переходит в жидкую.

Чтобы найти критические параметры, воспользуемся свойствами точки перегиба: первая и вторая производная уравнения обращаются в нуль.

Решим эти уравнения относительно объема и температуры, получим критические параметры:

Выразив давление из уравнения Ван-дер-Ваальса и записав это уравнение для критических параметров, получим:

Подставим в это уравнение , и после решения получим:

Запишем систему уравнений:

Найдем из нее b:

м 3 /моль.

Подставив b во второе уравнение системы, получим:

Па•м 6 /моль 2 .

Источник

Как вывести уравнение ван дер ваальса

Уравнение Ван–дер–Ваальса (7.1.2) – одно из первых уравнений состояния реального газа. Данное уравнение учитывает конечные размеры всех молекул, что становится существенным при больших давлениях, а также притяжение молекул в результате межмолекулярного взаимодействия.

Уравнение состояния реального газа, предложенное Ван–дер–Ваальсом можно получить из следующих рассуждений. Учтем влияние конечных размеров молекул на уравнение состояния реального газа. Давление определяется средней кинетической энергией теплового движения всех молекул Р = nkT. 7.2.1 При конечных размерах молекул, имеющих радиус r, область 4p(2r) 3 /3 вокруг каждой из молекул будет недоступна для попадания в нее другой неточечной молекулы. В результате в сосуде, содержащем N молекул конечных размеров, область объемом (N/2)4p(2r) 3 /3 = 4NV_молек (V_молек = 4pr 3 /3 – объем одной молекулы) будет недоступна для столкновений. Поэтому можно считать, что половина всех молекул занимает объем b = 4NV_молек и покоится, а другая половина представляет собой точечные молекулы и движется с удвоенной кинетической энергией, обладая температурой Т´ = 2Т. Объем, доступный точечным молекулам, будет равен V — b, а давление, оказываемое на стенки сосуда, определяется точечными подвижными молекулами (N´ = N/2):

Р = n´kT´ =

Если в сосуде находится один моль газа, то уравнение состояния примет вид (N = N_A, N_Ak = R, b = 4N_AV_молек):

Для v = m/m молей газа уравнение состояния газа с учетом конечного размера молекул примет вид

Отметим, что это уравнение является приближенным и выведено в предположении только парных столкновений. При больших давлениях это условие уже не выполняется, и возможно одновременное соприкосновение трех и более частиц, а такие случаи были исключены из рассмотрения.

Рассмотрим теперь влияние сил притяжения на уравнение состояния идеального газа. Будем считать для простоты частицы газа точечными. Наличие сил притяжения между ними, действующих на больших расстояниях, приводит к появлению дополнительного внутреннего воздействия на газ. Это обусловлено тем, что в то время как в объеме газа действие сил притяжения между молекулами в среднем уравновешивается, на границе «газ – стенка сосуда» действие сил притяжения со стороны газа остается не скомпенсированным, и появляется избыточная сила, направленная в сторону газа (рис. 7.3).

В результате избыточное внутреннее давление P_i (i — intrinsic) будет пропорционально квадрату концентрации числа частиц

где N – полное число частиц в сосуде объема V. Если N = N_A – в сосуде находится один моль газа, то запишем

P_i = a/V 2 ,
где а – постоянная величина, своя для каждого сорта газа. В случае v-молей имеем

С учетом внутреннего давления уравнение состояния примет вид

Давление P_i не зависит от материала стенки, в противном случае удалось бы создать вечный двигатель первого рода. Роль стенки может играть и сам газ. Достаточно для этого выполнить мысленное сечение произвольной плоскостью любой внутренней области объема газа. Полученное уравнение, с учетом выражения для P_i переходит в новое уравнение состояния реального газа при наличии сил притяжения:

(P + v 2 a/V 2 )V = vRT.

Учитывая совместное действие сил притяжения и сил отталкивания и полученные поправки для объема и давления в уравнении Менделеева – Клапейрона, получим уравнение Ван–дер–Ваальса для реального газа:

(P + v 2 a/V 2 )(V — vb) = vRT, (7.2.3)

Источник

Как вывести уравнение ван дер ваальса

Состояние определенной массы любого вещества можно описать с помощью трех параметров: давления \(p\) , объема \(V\) и температуры \(T\) . Эти параметры связаны между собой. Их взаимосвязь описывается уравнением состояния , которое в общем случае имеет вид: \[F\left( \right) = 0.\] Конкретный вид уравнения зависит от свойств вещества. Например, разреженный газ при достаточно высокой температуре хорошо описывается моделью идеального газа . Уравнением состояния для него является известное уравнение Клапейрона (\(1799-1864\)) , предложенное в \(1834\) году: \[pV = \fracRT.\] Здесь \(m\) − масса газа, \(M\) − молярная масса (т.е. масса одного моля данного газа), \(R\) − универсальная газовая постоянная. Для одного моля газа это уравнение принимает следующий вид: \[pV = RT.\] Проведенные позднее эксперименты выявили отклонение в поведении реальных газов от законов идеального газа. Эти результаты были обобщены голландским физиком Яном Дидериком Ван-дер-Ваальсом (\(1837-1923\)) , который в \(1873\) году предложил более точное уравнение состояния реального газа. Оно называется уравнением Ван-дер-Ваальса и в расчете на один моль записывается в виде \[\left(

>>> \right)\left( \right) = RT.\] Данное уравнение учитывает силы притяжения и отталкивания, действующие между молекулами. Силы притяжения учитываются благодаря пристеночному эффекту . Действительно, для частиц, находящихся во внутренней области, силы притяжения со стороны других молекул в среднем скомпенсированы. Однако для частиц вблизи стенок сосуда возникает нескомпенсированная сила притяжения \(f,\) направленная внутрь сосуда. Эта сила, с одной стороны, пропорциональна концентрации частиц \(n\) в сосуде, а с другой стороны − пропорциональна концентрации частиц в пристеночном слое. В результате получаем: \[f \sim \sim \frac<1><<>>,\] где \(n\) − концентрация молекул в сосуде, \(V\) − объем \(1\) моля газа.

Рассмотренный эффект притяжения молекул пристеночного слоя приводит к уменьшению давления на стенки сосуда. При формальном переходе от уравнения Клапейрона к уравнению Ван-дер-Ваальса это соответствует замене \[p \to p + \frac<<>>,\] где \(a\) − коэффициент, зависящий от конкретного газа и размеров сосуда.

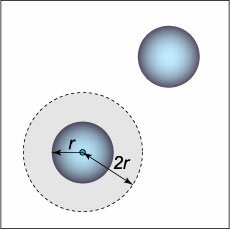
Силы отталкивания между молекулами в модели Ван-дер-Ваальса учитываются очень просто: предполагается, что молекулы имеют форму шара радиуса \(r\) и не могут приблизиться друг к другу на расстояние между центрами, меньшее чем \(2r.\) Можно считать, что вокруг одной из двух молекул существует «запрещенный» (исключенный) объем (рисунок \(1\)), равный \[\frac<4><3>\pi <\left( <2r>\right)^3> = 8 \cdot \frac<4><3>\pi .\] Следовательно, в расчете на одну молекулу исключенный объем равен \[ = 4 \cdot \frac<4><3>\pi = 4,\] где \(\) − объем одной молекулы.

В результате , если в уравнении Клапейрона объем пространства, доступного для движения молекул, был равен \(V,\) то теперь он становится равным \[V — = V — b,\] где \(\) − число Авогадро (равное числу молекул в одном моле газа), \(b\) − исключенный объем, обусловленный отталкиванием молекул.

Предполагая, что силы притяжения и отталкивания молекул действуют совместно и заменяя \(p\) и \(V\) новыми выражениями, получаем из уравнения Клапейрона уравнение Ван-дер-Ваальса: \[\left(

>>> \right)\left( \right) = RT.\]

Источник