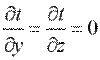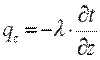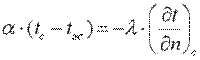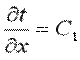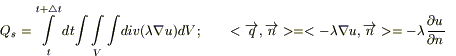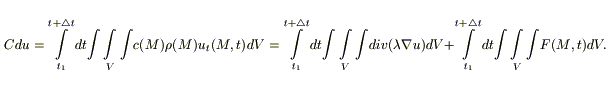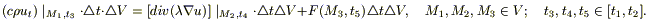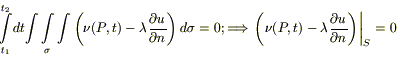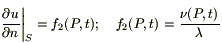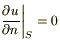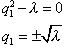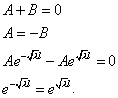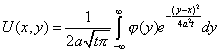Электронная библиотека
Рассмотрим однородный стержень (под стержнем в механике понимается тело с одним превалирующим линейным размером, например, столб можно рассматривать как стержень с переменным сечением) постоянного поперечного сечения S и длины l, теплоизолированный с боков, ось которого примем за ось Ох (рис. 4.3). Обозначим через U(x,t) температуру стержня в сечении с абсциссой х в момент времени t (предполагается, что во всех точках любого поперечного сечения стержня температура одна и та же.
Пусть – плотность стержня, – его удельная теплоемкость (это количество калорий, которое необходимо, чтобы единицу массы стержня нагреть на 1 ºС), – коэффициент теплопроводности (он представляет собой количество тепла в калориях, которое будет протекать за единицу времени через сечение стержня, если температура стержня падает на 1 ºС при перемещении вдоль стержня на единицу длины), – интенсивность теплового источника, находящегося в сечении х для момента t, отнесенная к единице массы и единице времени (т.е. количество тепла, создаваемого этим источником тепла за единицу времени и приходящегося на единицу массы; например, лампочку включенную в помещении, аппаратуру, работающую на космическом корабле и др. можно рассматривать как источники тепла;). Температуру же U(x, 0) стержня в начальный момент времени мы считаем известной и обозначим её через :
Тепловой режим на концах стержня может быть весьма разнообразен, т.е. температура может быть и постоянной, и изменяться, например, по законам: и др.). Мы рассмотрим два случая:
1) концы стержня поддерживаются при постоянной нулевой температуре:
2) концы стержня находятся в той же теплоизолирующей оболочке, что и весь стержень. Это означает, что через концы не происходит протекание тепла.
Рассмотрим сечение х нашего стержня и найдем, какое количество Q тепла протечет (слева направо) через это сечение за элементарный промежуток времени . В момент t температура стержня в точке х будет равна . Возьмем отличную от точки х точку x + dx стержня (пусть для определенности dx > 0) согласно закону Фурье количество тепла, протекающего в направлении оси Ох за бесконечно малый промежуток времени dt через сечение S с абсциссой х, будет:
где k – коэффициент теплопроводности ( представляет здесь величину градиента температуры U). Во формуле (4.37) стоит знак минус, так как при , т.е. при росте U вместе с х, поток тепла направлен в противоположную сторону, и наоборот).
Составим тепловой баланс для элемента , заключенную между бесконечно близкими сечениями х и x + dx. Предположим для определенности, что U возрастает в направлении Ох.
Тогда через сечение с абсциссой х тепло выходит, а через сечение с абсциссой x + dx входит. Пусть dQ есть количество тепла, накопленное нашим элементом за время dt. Тогда количество тепла, созданное за dt источниками тепла в элементе равно:
Используя формулу (4.37) будем иметь:
Применяя формулу Лагранжа из дифференциального исчисления с точностью до бесконечно малых высшего порядка малости, получим:
Следовательно, формула (4.39) примет вид:
С другой стороны, есть скорость изменения температуры элемента , и поэтому представляет собой изменение его температуры. Так как масса элемента равна , то накопленное при этом количество тепла будет:
Итак, сравнивая (4.41) и (4.40), после сокращения получим:
или, обозначая (величина а называется коэффициентом температуропроводности), окончательно получим дифференциальное уравнение, описывающее распределение температуры U(x,t) в стержне и носит название уравнения теплопроводности:
Если источники тепла отсутствуют, то уравнение (4.43) принимает вид уравнения свободного теплообмена в стержне:
Аналогичным образом можно вывести уравнения для распространения температуры в пластине:
где – оператор Лапласа (см. разд. 1.4.6).
Вывод: уравнение теплопроводности есть уравнение с частными производными второго порядка, параболического типа, так как ; в процессе вывода уравнения теплопроводности мы пришли к двум математическим задачам:
1) Найти то решение уравнения (4.44), которое удовлетворяет начальному условию (4.35) и граничным условиям (4.36).
2) Найти то решение уравнения (4.44), которое удовлетворяет начальному условию (4.35) и граничным условиям:
т.е. когда концы стержня теплоизолированы (количество тепла, протекающее через них, равно нулю).
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Источник
уравнение теплопроводности. поток тепла. коэффициенты теплопроводности и температуропроводности. Начальное условие



ЧАСТЬ 2. ТЕПЛОМАССООБМЕН Тема 9. ТЕПЛОПРОВОДНОСТЬ
9.1.Основные понятия и определения
Теория теплопередачи, или теплообмена, представляет собой учение о процессах распространения теплоты в пространстве с неоднородным полем температур.
Существуют три основных вида теплообмена: теплопроводность, конвекция и тепловое излучение.
Теплопроводность — это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).
Конвекция осуществляется путем перемещения в пространстве неравномерно нагретых объемов среды. При этом перенос теплоты неразрывно связан с переносом самой среды.
Тепловое излучение характеризуется переносом энергии от одного тела к другому электромагнитными волнами.
Часто все способы переноса теплоты осуществляются совместно. Например, конвекция всегда сопровождается теплопроводностью, так как при этом неизбежно соприкосновение частиц, имеющих различные температуры.
Совместный процесс переноса теплоты конвекцией и теплопроводностью называется конвективным теплообменом. Частным случаем конвективного теплообмена является теплоотдача — конвективный теплообмен между твердой стенкой и движущейся средой. Теплоотдача может сопровождаться тепловым излучением. В этом случае перенос теплоты осуществляется одновременно теплопроводностью, конвекцией и тепловым излучением.
Многие процессы переноса теплоты сопровождаются переносом вещества — массообменном, который проявляется в установлении равновесной концентрации вещества.
Совместное протекание процессов теплообмена и массообменна называетсятепломассообменном.
Теплопроводность определяется тепловым движением микрочастиц тела. В чистом виде явление теплопроводности наблюдается в твердых телах, неподвижных газах и жидкостях при условии невозможности возникновения в них конвективных токов.
Передача теплоты теплопроводностью связана с наличием разности температур тела. Совокупность значений температур всех точек тела в данный момент времени называется температурным полем. В общем случае уравнение температурного поля имеет вид:
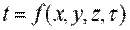
где t — температура тела; х, у, z — координаты точки; τ — время. Такое температурное поле называется нестационарным и отвечает неустановившемуся режиму теплопроводности. Если температура тела не изменяется с течением времени, то температурное поле называется стационарным. Тогда
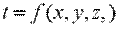
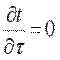
Температура может быть функцией одной, двух и трех координат, соответственно температурное поле будет одно-, дву- и трехмерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:
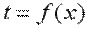
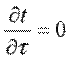
Если соединить все точки тела с одинаковой температурой, то получим поверхность равных температур, называемую изотермической. Так как в определенной точке тела в данный момент времени может быть только одна температура, изотермические поверхности не пересекаются; все они либо замыкаются на себя, либо заканчиваются на границе тела. Пересечение изотермных поверхностей плоскостью дает на ней семейство изотерм. Интенсивность изменения температуры в каком-либо направлении характеризуется производной 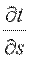
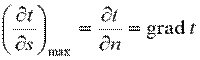
Вектор 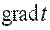
Согласно гипотезе Фурье, количество теплоты d 2 Qτ, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту 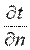
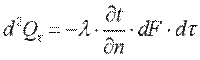
Здесь множитель λ называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении уменьшения температуры. Количество теплоты, прошедшее в единицу времени через единицу изотермической поверхности, называется плотностью теплового потока:
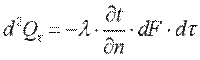

Проекции вектора q на координатные оси соответственно:
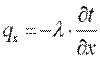
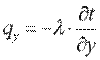
Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.
Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком: 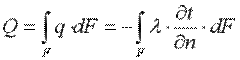
Полное количество теплоты, прошедшее через эту поверхность за время τ, определится из уравнения 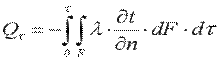
Коэффициент теплопроводности является физическим параметром вещества, характеризующим его способность проводить теплоту. Коэффициент теплопроводности определяется из уравнения (9.4):
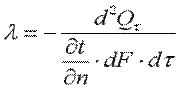
Численно коэффициент теплопроводности равен количеству теплоты, проходящему в единицу времени через единицу изотермической поверхности при условии gradt=1. Его размерность Вт/(м·К). Значения коэффициента теплопроводности для различных веществ определяются из справочных таблиц, построенных на основании экспериментальных данных. Для большинства материалов зависимость коэффициента теплопроводности от температуры приближенно можно выразить в виде линейной функции
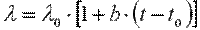
где λ0 — значение коэффициента теплопроводности при температуре t0=0 0 С; b — постоянная, определяемая опытным путем.
Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и составляет 0,006÷0,6 Вт/(м·К). Следует отметить, что верхнее значение относится к гелию и водороду, коэффициент теплопроводности которых в 5—10 раз больше, чем у других газов. Коэффициент теплопроводности воздуха при 0 0 С равен 0,0244 Вт/(м·К).
Для жидкости λ=0,07÷0,7 Вт/(м·К) и, как правило, уменьшается с увеличением температуры. Коэффициент теплопроводности воды с увеличением температуры возрастает до максимального значения 0,7 Вт/(м·К) при t=120 0 С и дальше уменьшается.
Наилучшими проводниками теплоты являются металлы, у которых λ=20÷418 Вт/(м·К). Самый теплопроводный металл — серебро. Для большинства металлов коэффициент теплопроводности убывает с возрастанием температуры, а также при наличии разного рода примесей. Поэтому коэффициент теплопроводности легированных сталей значительно ниже, чем чистого железа.
Материалы с λ 2 ·К). Коэффициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду, 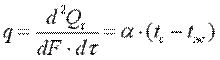
Согласно закону сохранения энергии, эта теплота равна теплоте, подводимой к поверхности изнутри тела путем теплопроводности:
Переписав последнее уравнение в виде:
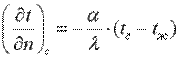
получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.
9.4.3.Теплопроводность через плоскую стенку при граничных условиях первого рода
 |
| Рис. 9.2. Однородная плоская стенка |
Рассмотрим однородную плоскую стенку толщиной δ (рис. 9.2). На наружных поверхностях стенки поддерживаются постоянные температуры tс1 и tс2. Коэффициент теплопроводности стенки постоянен и равен λ. При стационарном режиме ( 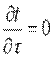
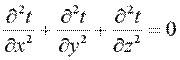
При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки (ось Оx). В этом случае 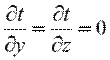
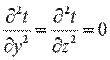
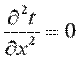
После второго интегрирования получаем 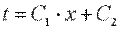
Постоянные С1 и С2 определим из граничных условий: при x=0 t=tc1, С2=tc1; приx=δ t=tc2=С1·δ+tc1, отсюда 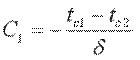
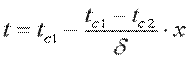
Для определения плотности теплового потока, проходящего через стенку в направлении оси Оx, воспользуемся законом Фурье, согласно которому 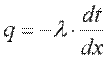
Учитывая, что 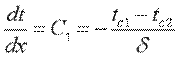
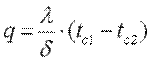
Общее количество теплоты, которое передается через поверхность стенки F за время τ,
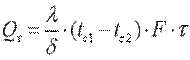
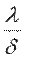
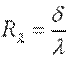
ТЕПЛОВОЙ ПОТОК — количество теплоты, переданное через изотермическую поверхность в единицу времени.
Т.П.количество теплоты, переданное через изотермическую поверхность в единицу времени. РазмерностьТ. п. совпадает с размерностью мощности (См. Мощность). Т. п. измеряется в Ваттахили ккал/ч (1 вт = 0,86ккал/ч).Т. п., отнесённый к единице изотермической поверхности, называется плотностью Т. п., удельным Т.п. или тепловой нагрузкой; обозначается обычно q, измеряется в вт/м 2 или ккал/(м 2 ․ч). Плотность Т. п. —вектор, любая компонента которого численно равна количеству теплоты, передаваемой в единицу временичерез единицу площади, перпендикулярной к направлению взятой компоненты.
Температуропроводность (коэффициент температуропроводности) — физическая величина, характеризующая скорость изменения (выравнивания)температуры вещества в неравновесных тепловых процессах. Численно равна отношению теплопроводности к объёмной теплоёмкости при постоянномдавлении, в системе СИ измеряется в м²/с.
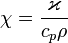
где 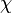
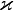
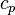
Температуропроводность и теплопроводность являются двумя из наиболее важных параметров веществ и материалов, поскольку они описывают процесс переноса теплоты и изменение температуры в них.
Величина коэффициента температуропроводности зависит от природы вещества. Жидкости и газы обладают сравнительно малой температуропроводностью. Металлы, напротив, имеют бо́льший коэффициент температуропроводности.
Коэффициент температуропроводности в тепловых процессах характеризует скорость изменения температуры. [2]
Коэффициент температуропроводности ( а) — служит мерой скорости, с которой пористая среда передает изменение температуры с одной точки в другую. [3]
Коэффициент температуропроводности характеризует скорость выравнивания температуры ( тепловую инертность) тела и по аналогии с коэффициентом диффузии, с которым он имеет одинаковую размерность, иногда называется коэффициентом тепловой диффузии. [4]
Вывод уравнения теплопроводности:
Рассмотрим задачу о распространении тепла в неревномерно нагретом твердом теле. В качестве величины, 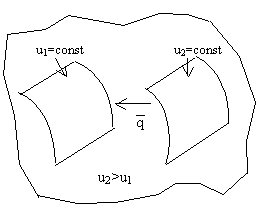
Посмотреть определения потока и дивергенции векторного поля
1) Будем рассматривать процесс распространения тепла посредством теплопроводности (т.е. при непосредственном контакте областей с разной температурой).
2) Для теплообмена посредством теплопроводности необходимо наличие ненулевого температурного градиента, т.е. различные части тела должны иметь разную температуру. При этом, так как каждая система стремится к своему равновесному состоянию, происходит переток тепла от более «нагретых» частей тела к более «холодным».
3) Для математического описания полей тепловых потоков введем в рассмотрение вектор плотности теплового потока 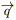
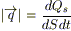
4) В основе аналитической теории теплопроводности лежит экспериментально установленный закон Фурье, согласно которому 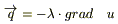
5) Будем считать, что наше изучаемое тело изотропно, т.е. λ = λ(x,y,z) и не зависит от выбора нормали к поверхности; 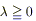
6) По определению потока для вектора 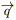
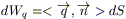
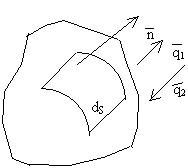
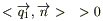
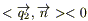
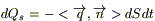
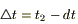
(1)
7) Предположим, что внутри нашего объема есть источники тепла. Обозначим через F(M,t) — плотность тепловых источников (количество тепла, выделяемое в единице объема за единицу времени). Тогда во всем объеме V за время 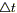
(2) 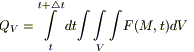
8) В соответствии с 1 м началом термодинамики тепло, получаемое системой идет на изменение ее температуры и на совершение этой системой работы: Q = Cdu + δA. Будем считать, что δA= 0 (для твердых тел).
du — изменение температуры за время 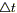
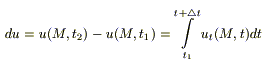
C — теплоемкость объема V, может быть расписана через удельную теплоемкость с, плотность вещества p и объем V: CdV = c(M)r(M)dV — для элементарного объема dV. Тогда
(3) 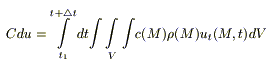
В наш выделенный объем тепло δQ поступает за счет 2 x механизмов: переноса тепла через поверхность, и возникновения тепла за счет работы источников).
Подставим (1), (2), (3):
Применим теорему о среднем значении (дважды: по t и по V) к каждому из этих интегралов:
Поделим полученное соотношение на ( 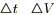
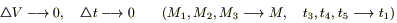
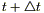
(1) 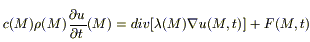
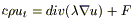
Если среда однородна, то λ,c,p — const и λ можно вынести из под функции div,и, поделив на (cp), получим:
(1a) 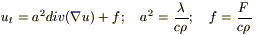
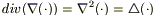
(1б) 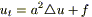
Если 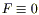
Рассмотрим теперь дополнительные условия, необходимые для однозначного решения задачи:
а) Необходимо знать начальное распределение температуры:
б) Тепловой режим на границе. Основные виды тепловых режимов:
I. — на границе поддерживается определенная температура
II. — через границу подается определенный тепловой поток
III. — происходит теплообмен с внешней средой, температура которой известна.
Разберем более подробно каждый из типов:
II. Обозначим через ν(P,t) — плотность теплового потока на границе S. (Количество тепла, проходящего через единицу площади за единицу времени).
Пусть σ — произвольный участок поверхности S, ограниченный замкнутой гладкой кривой.
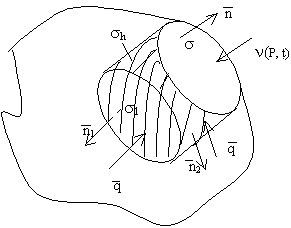
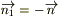
Для записи 1 го начала термодинамики (закон сохранении энергии):
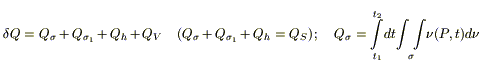
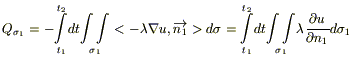
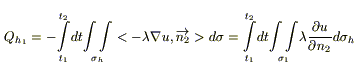
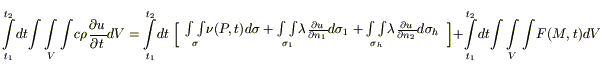
при 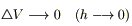
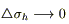
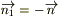
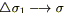
Применяя дважды теорему о среднем (по t и по σ), устремляя 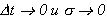
(3б)
Если поверхность S теплоизолирована (ν = 0):
III. Будем считать, что теплообмен между телом и окружающей средой происходит по закону Ньютона: плотность теплового потока ν(P,t), получаемого из внешней среды, пропорциональна разности температуры окружающей среды θ(t) и температуры u внутри V вблизи поверхности S.
Таким образом, мы имеем случай II, где ν(P,t) имеем специфический вид (*), т.е. 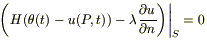
(3в) 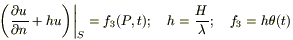
В случае, если температура окружающей среды θ(t) = 0, получим однородное граничное условие 3 го рода: 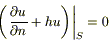
Таким образом, мы приходим к задаче: найти решение уравнения теплопроводности (1), удовлетворяющее нормальным условиям (2) и одному из граничных условий (3). Совершенно аналогично ставятся задачи в одномерном и двумерном случаях. Для уравнения (1) можно также поставить задачу Коши (т.е. задачу без граничных условий)
Замечание: к уравнению (1) приводятся и другие физические задачи: уравнение диффузии, движение вязкой жидкости.
2.1. Метод разделения переменных для конечного стержня
Уравнение теплопроводности относится к уравнениям параболического типа.
Уравнение теплопроводности имеет вид:

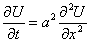

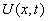
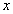
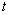

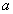
Рассмотрим однородный стержень длины 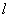
Для выделения единственного решения уравнения теплопроводности необходимо к уравнению присоединить начальные и граничные условия. Для задач этого типа задается только одно начальное условие, а именно, начальная температура в начальный момент времени. Итак,
 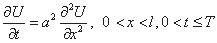 . . | (1) |
 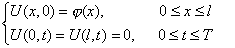 , , | (2) (3) |
где 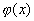
Концы стержня закреплены в термостате. В данном случае тепловая энергя стержня не сохраняется, так как система не является изолированной.
Будем искать решение в виде произведения двух функций

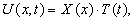
где X(x)- функция только переменного x,


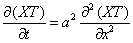

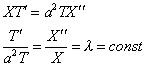
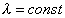

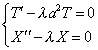
Граничные условия (3) дают:

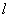
тогда
 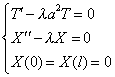 | (4) (5) (6) |
Необходимо определить знак 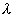
1 случай: Пусть 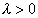
Рассмотрим уравнение (4):

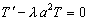
Характеристическое уравнение имеет вид:

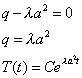
Рассмотрим уравнение (5):

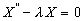
Характеристическое уравнение имеет вид:
 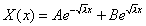 . . | (7) |
Это решение не подходит, так как если 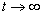
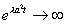
Значит 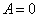
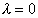
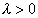
2 случай: Пусть 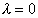
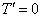
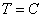
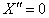
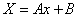
Подставим краевые условия
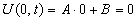
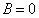
В итоге получим нулевое решение 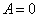
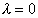
3 случай: Пусть 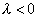
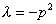

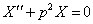
Характеристическое уравнение имеет вид:
Общее решение может быть записано в виде:
 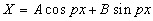 . . | (8) |
Подставим краевые условия.

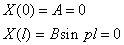
Получаем
 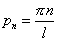 . . | (9) |
Существуют нетривиальные решения уравнения (5), равные
 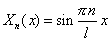 . . | (10) |
Этим значениям 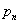

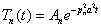
где 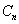
 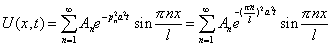 | — общее решение. |
Удовлетворим начальным условиям (2):

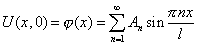
Для выполнения этого начального условия необходимо взять в качестве 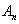

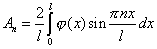
Для получения ответа необходимо подставить указанный коэффициент в общее решение задачи.
Уравнение теплопроводности для бесконечного стержня
Рассмотрим задачу с начальными данными на бесконечной прямой. А именно, найдем ограниченную функцию, 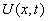
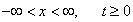
 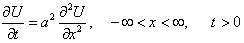 |
и начальному условию
 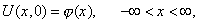 |
где функция 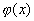
Сделаем преобразование Фурье по переменной 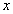

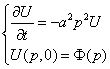

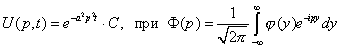

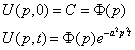
Чтобы получить итоговое решение, нужно провести обратное преобразование Фурье

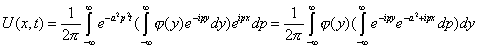

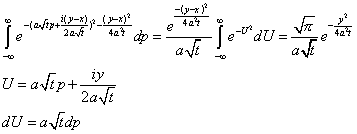
Тогда общее решение имеет вид
 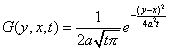 | — функция Грина для уравнения теплопроводности. |
 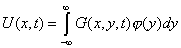 | — общее решение (стандартный вид). |
Эта функция дает решение уравнения теплопроводности с заданным начальным условием.
Источник