Как вывести функцию если даны 2 точки

Как решать задачи на функцию

Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».

После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.

В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.

Как получить значение функции

Рассмотрим задание. Функция задана формулой « y = 2x − 1 »

1. Вычислить « y » при « x = 15 »
2. Найти значение « x », при котором значение « y » равно « −19 ».

Для того, чтобы вычислить « y » при « x = 15 » достаточно подставить в функцию вместо « x » необходимое числовое значение.

Запись решения выглядит следующим образом.

Для того, чтобы найти « x » по известному « y », необходимо подставить вместо « y » в формулу функции числовое значение.

То есть теперь наоборот, для поиска « x » мы подставляем в функцию « y = 2x − 1 » вместо « y » число « −19 » .

Мы получили линейное уравнение с неизвестным « x », которое решается по правилам решения линейных уравнений.

Не забывайте про правило переноса в уравнениях.

При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на противоположный .

Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас требуется умножить и левую, и правую часть на « −1 » для смены знака.

Теперь разделим и левую, и правую часть на « 2 », чтобы найти « x » .

Как проверить верно ли равенство для функции

Рассмотрим задание. Функция задана формулой « f(x) = 2 − 5x ».

Верно ли равенство « f(−2) = −18 »?

Чтобы проверить верно ли равенство, нужно подставить в функцию « f(x) = 2 − 5x » числовое значение « x = −2 » и сопоставить с тем, что получится при расчетах.

Когда подставляете отрицательное число вместо « x », обязательно заключайте его в скобки.

Не забывайте использовать правило знаков.

Неправильно

Правильно

С помощью расчетов мы получили « f(−2) = 12 ».

Это означает, что « f(−2) = −18 » для функции « f(x) = 2 − 5x » не является верным равенством.

Как проверить, что точка принадлежит графику функции

Рассмотрим функцию « y = x 2 −5x + 6 »

Требуется выяснить, принадлежит ли графику этой функции точка с координатами (1; 2) .

Для этой задачи нет необходимости, строить график заданной функции.

Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (координату по оси « Ox » вместо « x » и координату по оси « Oy » вместо « y »).

Если получится верное равенство , значит, точка принадлежит функции.

Вернемся к нашему заданию. Подставим в функцию « y = x 2 − 5x + 6 » координаты точки (1; 2) .

Вместо « x » подставим « 1 ». Вместо « y » подставим « 2 ».

У нас получилось верное равенство, значит, точка с координатами (1; 2) принадлежит заданной функции.

Теперь проверим точку с координатами (0; 1) . Принадлежит ли она
функции « y = x 2 − 5x + 6 »?

Вместо « x » подставим « 0 ». Вместо « y » подставим « 1 ».

В этом случае мы не получили верное равенство. Это означает, что точка с координатами (0; 1) не принадлежит функции « y = x 2 − 5x + 6 »

Как получить координаты точки функции

С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат в формулу функции получается верное равенство.

Рассмотрим функцию « y(x) = −2x + 1 ». Её график мы уже строили в предыдущем уроке.

Найдем на графике функции « y(x) = −2x + 1 », чему равен « y » при x = 2 .

Для этого из значения « 2 » на оси « Ox » проведем перпендикуляр к графику функции. Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси « Oy ».

Полученное значение « −3 » на оси « Oy » и будет искомым значением « y ».

Убедимся, что мы правильно сняли координаты точки для x = 2
в функции « y(x) = −2x + 1 ».

Для этого мы подставим x = 2 в формулу функции « y(x) = −2x + 1 ». Если мы правильно провели перпендикуляр, мы также должны получить в итоге y = −3 .

При расчетах мы также получили y = −3 .

Значит, мы правильно получили координаты с графика функции.

Все полученные координаты точки с графика функции обязательно проверяйте подстановкой значений « x » в функцию.

При подстановке числового значения « x » в функцию в результате должно получиться то же значение « y », которое вы получили на графике.

При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».

Только подстановка значений в формулу функции дает точные результаты.

Источник

Уравнение прямой по двум точкам

Как известно, через любые две точки на плоскости проходит прямая, и только одна. Напишите функцию equation(), которая по двум заданным точкам находит уравнение прямой, проходящей через них. На вход подаются две строки — координаты точек в формате x;y, функция должна выводить два числа через пробел — коэффициенты k и b найденной прямой. Если в решении получается прямая вида y=c или x=c, функция должна печатать эту константу с.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Уравнение прямой по двум точкам
#include using namespace std; void main() < setlocale (LC_ALL, "rus"); int x1.

Определить функцию, позволяющую построить уравнение прямой по двум точкам
Определить функцию, позволяющую построить уравнение прямой по двум точкам. как это вообще? 🙁

Как найти угол поворота прямой, по двум точкам другой прямой?
Здравствуйте, не думаю что правильно сформулировал заголовок темы, но стоит следующая задача: .

Вывести функцию прямой по двум точкам
Необходимо вывести функцию прямой по двум точкам, у меня получился следующий код: import.

Источник

Использование ЕСЛИ с функциями И, ИЛИ и НЕ

Функция ЕСЛИ позволяет выполнять логические сравнения значений и ожидаемых результатов. Она проверяет условие и в зависимости от его истинности возвращает результат.

=ЕСЛИ(это истинно, то сделать это, в противном случае сделать что-то еще)

Но что делать, если необходимо проверить несколько условий, где, допустим, все условия должны иметь значение ИСТИНА или ЛОЖЬ ( И), только одно условие должно иметь такое значение ( ИЛИ) или вы хотите убедиться, что данные НЕ соответствуют условию? Эти три функции можно использовать самостоятельно, но они намного чаще встречаются в сочетании с функцией ЕСЛИ.

Используйте функцию ЕСЛИ вместе с функциями И, ИЛИ и НЕ, чтобы оценивать несколько условий.

ЕСЛИ(И()): ЕСЛИ(И(лог_выражение1; [лог_выражение2]; …), значение_если_истина; [значение_если_ложь]))

ЕСЛИ(ИЛИ()): ЕСЛИ(ИЛИ(лог_выражение1; [лог_выражение2]; …), значение_если_истина; [значение_если_ложь]))

ЕСЛИ(НЕ()): ЕСЛИ(НЕ(лог_выражение1), значение_если_истина; [значение_если_ложь]))

Условие, которое нужно проверить.

Значение, которое должно возвращаться, если лог_выражение имеет значение ИСТИНА.

Значение, которое должно возвращаться, если лог_выражение имеет значение ЛОЖЬ.

Общие сведения об использовании этих функций по отдельности см. в следующих статьях: И, ИЛИ, НЕ. При сочетании с оператором ЕСЛИ они расшифровываются следующим образом:

И: =ЕСЛИ(И(условие; другое условие); значение, если ИСТИНА; значение, если ЛОЖЬ)

ИЛИ: =ЕСЛИ(ИЛИ(условие; другое условие); значение, если ИСТИНА; значение, если ЛОЖЬ)

НЕ: =ЕСЛИ(НЕ(условие); значение, если ИСТИНА; значение, если ЛОЖЬ)

Примеры

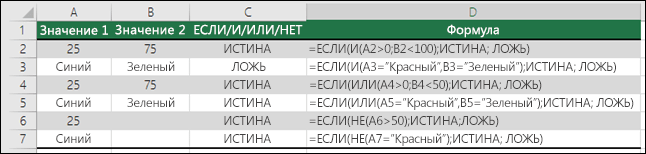
Ниже приведены примеры распространенных случаев использования вложенных операторов ЕСЛИ(И()), ЕСЛИ(ИЛИ()) и ЕСЛИ(НЕ()). Функции И и ИЛИ поддерживают до 255 отдельных условий, но рекомендуется использовать только несколько условий, так как формулы с большой степенью вложенности сложно создавать, тестировать и изменять. У функции НЕ может быть только одно условие.

Ниже приведены формулы с расшифровкой их логики.

=ЕСЛИ(И(A2>0;B2 0;B4 50);ИСТИНА;ЛОЖЬ)

Если A6 (25) НЕ больше 50, возвращается значение ИСТИНА, в противном случае возвращается значение ЛОЖЬ. В этом случае значение не больше чем 50, поэтому формула возвращает значение ИСТИНА.

Если значение A7 («синий») НЕ равно «красный», возвращается значение ИСТИНА, в противном случае возвращается значение ЛОЖЬ.

Обратите внимание, что во всех примерах есть закрывающая скобка после условий. Аргументы ИСТИНА и ЛОЖЬ относятся ко внешнему оператору ЕСЛИ. Кроме того, вы можете использовать текстовые или числовые значения вместо значений ИСТИНА и ЛОЖЬ, которые возвращаются в примерах.

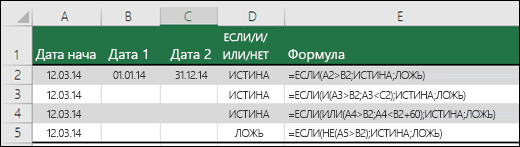
Вот несколько примеров использования операторов И, ИЛИ и НЕ для оценки дат.

Ниже приведены формулы с расшифровкой их логики.

Если A2 больше B2, возвращается значение ИСТИНА, в противном случае возвращается значение ЛОЖЬ. В этом случае 12.03.14 больше чем 01.01.14, поэтому формула возвращает значение ИСТИНА.

=ЕСЛИ(И(A3>B2;A3 B2;A4 B2);ИСТИНА;ЛОЖЬ)

Если A5 не больше B2, возвращается значение ИСТИНА, в противном случае возвращается значение ЛОЖЬ. В этом случае A5 больше B2, поэтому формула возвращает значение ЛОЖЬ.

Использование операторов И, ИЛИ и НЕ с условным форматированием

Вы также можете использовать операторы И, ИЛИ и НЕ в формулах условного форматирования. При этом вы можете опустить функцию ЕСЛИ.

На вкладке Главная выберите Условное форматирование > Создать правило. Затем выберите параметр Использовать формулу для определения форматируемых ячеек, введите формулу и примените формат.

«Изменить правило» с параметром «Формула»» loading=»lazy»>

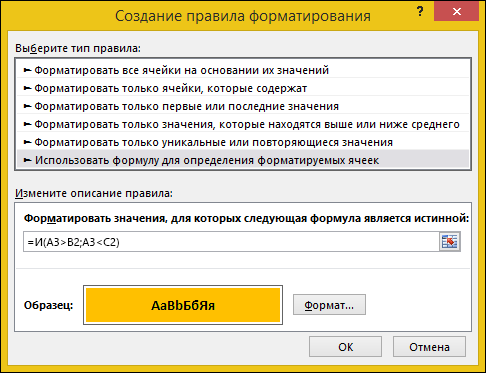
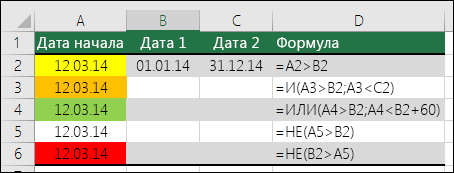
Вот как будут выглядеть формулы для примеров с датами:

Если A2 больше B2, отформатировать ячейку, в противном случае не выполнять никаких действий.

=И(A3>B2;A3 B2;A4 B2)

Если A5 НЕ больше B2, отформатировать ячейку, в противном случае не выполнять никаких действий. В этом случае A5 больше B2, поэтому формула возвращает значение ЛОЖЬ. Если изменить формулу на =НЕ(B2>A5), она вернет значение ИСТИНА, а ячейка будет отформатирована.

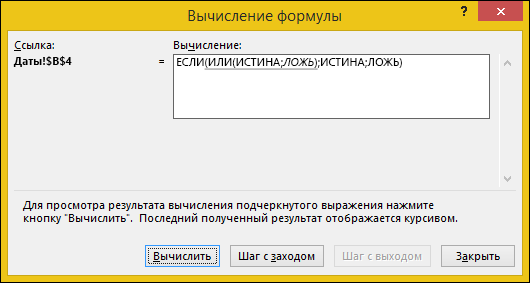
Примечание: Распространенная ошибка — ввод формулы в условное форматирование без знака «равно» (=). При этом вы увидите, что в диалоговом оке Условное форматирование в формулу будут добавлены знаки «равно» и кавычка: =»ИЛИ(A4>B2;A4

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Источник

Как вывести функцию если даны 2 точки

Ну вот и подошли к концу новогодние каникулы, а с ними и мое обучение по C++. Как говорил, закончил его с отличием. Сегодня рассмотрим задачи с использованием функций. Часть задач будет решаться с использованием рекурсивных функций. Напомню, что эти задачи рассматривались в курсе Введение в программирование (С++) на сайте steptic.org. Сейчас немного поделюсь новостями, а потом приступим к задачам.

Немного доработал сайт

• Сделал рубрикатор, за одно переделал состав рубрик. Добавил ссылку на рубрики на главную страницу.
• Немного доработал лайки. Теперь зарегистрированные пользователи не смогут их накрутить. Пока оставил возможность ставить лайки незарегистрированным пользователям, но теперь без возможности накрутки. Пришлось обнулить все лайки к статьям для функционирования новой механики.
• Сделал еще несколько небольших улучшений и поправил несколько ошибок.
• Регистрацию так и не удалось побороть, так что лучше регистрироваться через социальные сети.

Задача №1

Напишите функцию min(a, b) , вычисляющую минимум двух чисел. Затем напишите функцию min4(a, b, c, d) , вычисляющую минимум 4 чисел с помощью функции min . Считайте четыре целых числа и выведите их минимум.
Формат входных данных
Вводятся четыре целых числа.
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №2

Даны четыре действительных числа: $%x_1$%, $%y_1$%, $%x_2$%, $%y_2$%. Напишите функцию distance(x1, y1, x2, y2) , вычисляющую расстояние между точкой $%(x_1, y_1)$% и $%(x_2, y_2)$%. Считайте четыре действительных числа и выведите результат работы этой функции.
Формат входных данных
Вводятся четыре действительных числа.
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №3

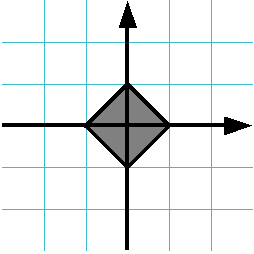
Даны два действительных числа $%x$% и $%y$%. Проверьте, принадлежит ли точка с координатами $%(x, y)$% заштрихованному квадрату (включая его границу). Если точка принадлежит квадрату, выведите слово YES , иначе выведите слово NO .

На рисунке сетка проведена с шагом 1.
Решение должно содержать функцию IsPointInSquare(x, y) , возвращающую true , если точка принадлежит квадрату и false , если не принадлежит. Основная программа должна считать координаты точки, вызвать функцию IsPointInSquare и в зависимости от возвращенного значения вывести на экран необходимое сообщение.
Функция IsPointInSquare не должна содержать инструкцию if .
Формат входных данных
Вводятся два действительных числа.
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №4

Даны пять действительных чисел: $%x$%, $%y$%, $%x_c$%, $%y_c$%, $%r$%. Проверьте, принадлежит ли точка $%(x, y)$% кругу с центром $%(x_c, y_c)$% и радиусом $%r$%. Если точка принадлежит кругу, выведите слово YES , иначе выведите слово NO .
Решение должно содержать функцию IsPointInCircle(x, y, xc, yc, r) , возвращающую True , если точка принадлежит кругу и False , если не принадлежит.
Основная программа должна считать координаты точки, вызвать функцию IsPointInCircle и в зависимости от возвращенного значения вывести на экран необходимое сообщение.
Функция IsPointInCircle не должна содержать инструкцию if .
Формат входных данных
Вводятся пять действительных чисел.
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №5

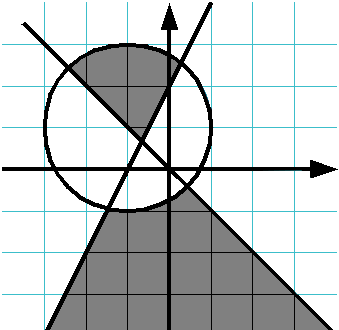
Проверьте, принадлежит ли точка данной закрашенной области:

Если точка принадлежит области (область включает границы), выведите слово YES , иначе выведите слово NO .
Решение должно содержать функцию IsPointInArea(x, y) , возвращающую True , если точка принадлежит области и False , если не принадлежит. Основная программа должна считать координаты точки, вызвать функцию IsPointInArea и в зависимости от возвращенного значения вывести на экран необходимое сообщение.
Функция IsPointInArea не должна содержать инструкцию if .
Формат входных данных
Вводятся два действительных числа.
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №6

Дано действительное положительное число $%a$% и целоe число $%n$%. Вычислите $%a^n$%. Решение оформите в виде функции power(a, n) .
Формат входных данных
Вводится действительное положительное число $%a$% и целоe число $%n$%.
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №7

Дано натуральное число $%n > 1$%. Выведите его наименьший делитель, отличный от 1.
Решение оформите в виде функции MinDivisor(n) . Количество операций в программе должно быть пропорционально $%sqrt$%.
Указание
Если у числа $%n$% нет делителя, меньшего $%n$% , то число $%n$% — простое и ответом будет само число $%n$%.
Формат входных данных
Вводится натуральное число.
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №8

Дано натуральное число $%n > 1$%. Проверьте, является ли оно простым. Программа должна вывести слово YES , если число простое и NO , если число составное.
Решение оформите в виде функции IsPrime(n) , которая возвращает True для простых чисел и False для составных чисел. Количество операций в программе должно быть пропорционально $%/sqrt$%.
Формат входных данных
Вводится натуральное число.
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №9

Возводить в степень можно гораздо быстрее, чем за $%n$% умножений! Для этого нужно воспользоваться следующими рекуррентными соотношениями:
$%a^n = (a^2)^$%, при четном $%n$%,
$%a^n = a × a^$%, при нечетном $%n$%

Реализуйте алгоритм быстрого возведения в степень с помощью рекурсивной функции.
Формат входных данных
Вводятся действительное число a и целое неотрицательное число $%n$%.
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №10

Дана последовательность чисел, завершающаяся числом 0. Найдите сумму всех этих чисел, не используя цикл.
Формат входных данных
Вводится последовательность целых чисел, оканчивающаяся числом 0 (само число 0 в последовательность не входит, а служит как признак ее окончания).
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №11

Напишите функцию fib(n) , которая по данному целому неотрицательному $%n$% возвращает $%n$%-e число Фибоначчи. В этой задаче нельзя использовать циклы — используйте рекурсию.
Первое и второе числа Фибоначчи равны 1, а каждое следующее равно сумме двух предыдущих.
Формат входных данных
Вводится целое число.
Формат выходных данных
Выведите ответ на задачу.

Решение

Задача №12

Дано число N. Определите, сколькими способами можно расставить на доске $%N×N$% $%N$% ферзей, не бьющих друг друга.
Формат входных данных
Задано единственное число $%N$%. $%(N ≤ 10)$%
Формат выходных данных
Выведите ответ на задачу.

Источник