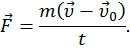Вывод закона сохранения импульса.
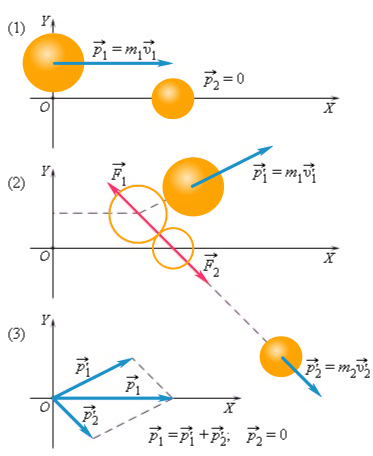
Второй закон Ньютона выражается формулой 
Если подставить это выражение в формулу, получим:

В правой части этого равенства записано изменение произведения массы тела на его скорость. Произведение массы тела на скорость является физической величиной, которая называется импульсом тела. Обозначим массы этих двух тел через m1 и m2, а их скорости относительно какой-либо системы отсчета через 






Изменим знаки обеих частей равенства на противоположные и запишем в виде

В левой части равенства – сумма начальных импульсов двух тел, в правой части – сумма импульсов тех же тел через время t. Суммы равны между собой. Таким образом, несмотря на то. что импульс каждого тела при взаимодействии изменяется, полный импульс (сумма импульсов обоих тел) остается неизменным.
Вопрос 11

Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.
Работа силы на конечном перемещении равна сумме ее работ на элементарных участках.
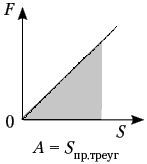
Работа силы на перемещении М1М2 изображается площадью фигуры, ограниченной осью абсцисс, кривой и ординатами, соответствующими точкам М1 и М0.
Единица измерения работы силы и кинетической энергии в системе СИ 1 (Дж).

Если F = const, то
Работой 
называется физическая величина, равная произведению модулей
силы и перемещения, умноженному на косинус угла 
Выражение показывает, что работа является скалярной величиной и может иметь положительное или отрицательное значение в зависимости от знака косинуса угла 
Работа, совершаемая силой 



Работа силы упругости — работа, совершаемая силой упругости при изменении деформации пружины от некоторого начального значения x1 до конечного значения x2
Вывод формулы работы силы упругости (через интеграл)

Найдем работу, совершаемую силами поля тяготения, созданного точечной массой М, при перемещении материальной точки с массой m. Силы тяготения являются консервативными силами, поэтому их работа не зависит от траектории, а лишь от начального и конечного положения тела. Работа сил тяготения по перемещению тела на малый вектор dr вдоль линии, соединяющей два тела, равна:

Вопрос 12
Мощность— физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. P=N=W ß буквы взаимозаменяемы.


P= 


= Вт [ватты] скалярная физическая величина.
Кинетическая энергия — скалярная функция, являющаяся мерой движения материальной точки и зависящая только от массы и модуля скорости материальных точек, образующих рассматриваемую физическую систему[1], энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта. Часто выделяют кинетическую энергию поступательного и вращательного движения[2].
Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением[3].
Простым языком, кинетическая энергия — это энергия, которую тело имеет только при движении. Когда тело не движется, кинетическая энергия равна нулю.
dA = F dr =m * 
dA=d( 

Вопрос 13
Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке (поле силы тяжести Земли). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.
Стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от траектории, а зависит только от положения этих точек, называется потенциальным, а сами силы – консервативными (F тяж, F упр).
Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными (F трения).
Свойства консервативных сил:
1) 
2) 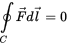
3) 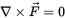
4) 
Таким образом, потенциальная сила всегда направлена в сторону уменьшения потенциальной энергии.
Вопрос 14
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Источник
Закон сохранения импульса. Реактивное движение
Закон сохранения импульса
Закон сохранения импульса можно наблюдать повсюду. Он достаточно точно выполняется в реальных условиях, если пренебречь сопротивлением воздуха, силами трения и т.д. Примеры проявления этого закона:
- стрелок ощущает отдачу при выстреле из ружья;
- рыбак переходит с кормы на нос лодки, а лодка при этом движется в противоположную сторону;
- шары сталкиваются на бильярдном столе.
Однако, прежде чем говорить о законе сохранении импульса, рассмотрим понятие замкнутой системы.
Замкнутая система — система тел, на которую со стороны других тел не действуют внешние силы.
Формулировка закона сохранения импульса (ЗСИ)
Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы.
Данный закон является следствием из второго и третьего законов Ньютона. Покажем это.
Возьмем замкнутую систему из двух взаимодействующих тел. Силы F 1 → и F 2 → — это силы взаимодействия между телами. Третий закон Ньютона гласит, что F 2 → = — F 1 → . Пусть тела взаимодействуют во течение времени t . Тогда импульсы сил одинаковы по модулю и противоположны по направлению, как и сами силы.
F 2 t → = — F 1 → t .
По второму закону Ньютона:
F 1 → t = m 1 v 1 ‘ → — m 1 v 1 → ; F 2 → t = m 1 v 2 ‘ → — m 1 v 2 →
Здесь v 1 ‘ → и v 2 ‘ → — скорости тел в конце взаимодействия. Соответственно, скорости без штрихов обозначают эти величины в начальный момент взаимодействия.
Из записанного выше следует соотношение:
m 1 v 1 → + m 2 v 2 → = m 1 v 1 ‘ → + m 2 v 2 ‘ →
Это равенство — математическая форма записи закона сохранения импульса. Оно означает, что суммарный импульс системы в результате какого-то взаимодействия не изменился.
Проиллюстрируем закон сохранения импульса на примере соударения шаров разных масс. Один из шаров до удара покоился.
Как видим, после удара векторная сумма импульсов двух шаров равна первоначальному импульсу движущегося шара.
Важно! Закон сохранения выполняется и для проекций векторов на координатные оси.
Закон сохранения импульса позволяет решать задачи и находить скорости тел не зная значений действующих сил.
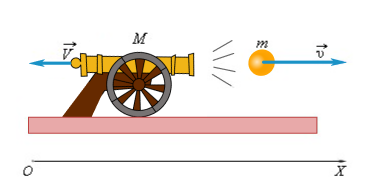
Рассмотрим снаряд, вылетающий из пушки.
В данном случае взаимодействующие тела — это снаряд и пушка. Сначала тела не движутся. При выстреле снаряд приобретает скорость v → и летит вперед, а пушка откатывается назад со скоростью V → . Откатывание пушки называется отдачей от выстрела.
По закону сохранения импульса в проекции на ось OX можно записать:
Реактивное движение
Реактивное движение также основано на принципе отдачи. Нагретые газы выбрасываются из сопла реактивного двигателя со скоростью u → . Пусть масса газов равна m , а масса ракеты после истечения газов — M . Рассматривая замкнутую систему «ракета-газы» и применяя к ней закон сохранения импульса, можно вычислить скорость ракеты V после истечения газов.
Формула для пушки и снаряда не применима к ракете, так как дает лишь приблизительное представление о движении ракеты, На самом деле вся масса газов выходит из сопла не сразу, а постепенно.
Рассмотрим этот процесс подробнее. Пусть масса ракеты в момент времени t равна M , а сама ракета движется со скоростью v → . В течение малого промежутка времени ∆ t из сопла ракеты выбрасывается порция газа с относительной скоростью u → . По истечении времени ∆ t ракета будет двигаться со скоростью v + ∆ v , а масса ракеты станет равной M — ∆ M .
В момент t + ∆ t импульс ракеты равен:
Импульс реактивных газов:
По закону сохранения импульса:
M v → = M — ∆ M · v → + ∆ v → + ∆ M · v → + u → .
M ∆ v → = ∆ M · u → — ∆ M · ∆ v → .
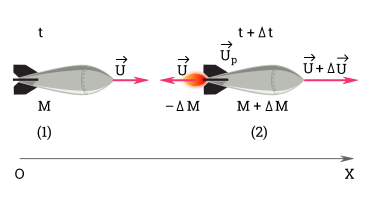
Величиной ∆ M · ∆ v → можно пренебречь, так как ∆ M намного меньше M .
Разделим последнее равенство на ∆ t и перейдем к пределу ∆ t → 0 .
M ∆ v → ∆ t = ∆ M · u → ∆ t ( ∆ t → 0 )
Здесь μ — расход топлива в единицу времени, а — μ u → — реактивная сила тяги. Направление этой силы совпадает с направлением движения ракеты.
Формула M a → = — μ u → выражает второй закон Ньютона для тела переменной массы. В скалярном виде ее можно переписать так:
Конечная скорость ракеты определяется по формуле:
Это так называемая формула Циолковского, согласно которой конечная скорость ракеты может превышать скорость истечения газов из сопла двигателя. Правда, достижение такой скорости связано с определенными сложностями. Во-первых, такими, как значительный расход топлива.
Для того, чтобы развить первую космическую скорость v = v 1 = 7 , 9 · 10 3 м с при скорости истечения газов u = 3 · 10 3 м с стартовая масса ракеты должна быть примерно в 14 раз больше конечной массы.
Современное ракетостроение развивается в направлении экономичных многоступенчатых ракет. Сброс отсеков с отработанным топливом позволяет значительно сократить массу ракеты и оптимизировать дальнейший расход топлива для ее разгона.
Источник