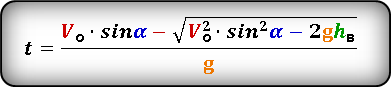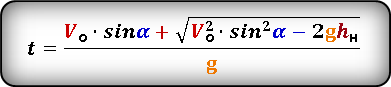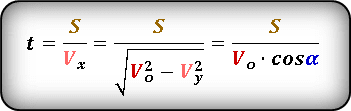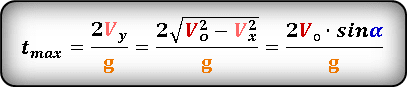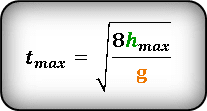Определить время полета тела брошенного под углом к горизонту
1. Найти время полета тела на определенной высоте
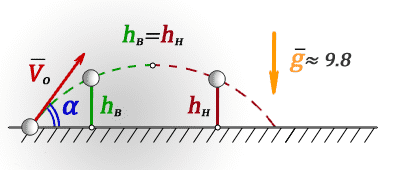
h в — высота на восходящем участке траектории
h н — высота на нисходящем участке траектории
t — время в момент которого тело находится на высоте h в или h н
V o — начальная скорость тела
α — угол под которым брошено тело
g ≈ 9,8 м/с 2 — ускорение свободного падения
Формула для определения значения времени , за которое тело поднялось на определенную высоту, на восходящем участке траектории
Формула для определения значения времени , за которое тело поднялось на определенную высоту, на нисходящем участке траектории
Таким образом, одному значению высоты будет соответствовать два значения времени, одно при подъеме, второе при падении.
2. Найти время полета тела пролетевшее определенное расстояние
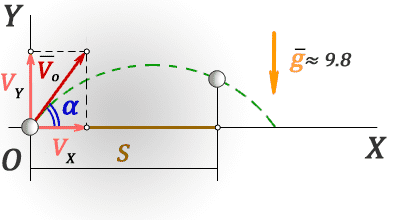
S — расстояние пройденное по горизонтали
t — время за которое тело прошло расстояние S
V o — начальная скорость тела
V x — проекция начальной скорости на ось OX
V y — проекция начальной скорости на ось OY
α — угол под которым брошено тело
g ≈ 9,8 м/с 2 — ускорение свободного падения
Формула для определения значения времени , за которое пройдено определенное расстояние
3. Значение времени при максимальных значениях высоты и дальности
S max — максимальная дальность по горизонтали
h max — максимальная высота
t max — время всего полета
t h — время за которое тело поднялось на максимальную высоту
V o — начальная скорость тела
V x — проекция начальной скорости на ось OX
V y — проекция начальной скорости на ось OY
α — угол под которым брошено тело
g ≈ 9,8 м/с 2 — ускорение свободного падения
Формула для определения значения времени , затраченное на весь полет, если известна начальная скорость или ее проекции
Формула для определения значения времени , на максимальной высоте
Т. к. траектория движения тела симметрична относительно линии максимальной высоты, следовательно — время всего полета, в два раза больше времени затраченного при подъеме на максимальную высоту
Источник
Как вывести формулу времени полета тела под углом
Цель работы: изучение движения тела, брошенного под углом к горизонту; определение времени, дальности и высоты полета.
Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения 
; проекции ускорения на координатные оси равны ах = 0, ау = -g.
Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).
Проекции скорости тела, следовательно, изменяются со временем следующим образом:
где 
– начальная скорость, α – угол бросания.
Координаты тела, следовательно, изменяются так:
При нашем выборе начала координат начальные координаты 
(рис. 1) Тогда
 | (1) |
Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:
 . | (2) |
Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл.
Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t0. Подставляя значение (2) в первую формулу (1), получаем:
 . | (3) |
Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.
Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем
 . | (4) |
Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:
и подставить его во второе уравнение. Тогда получим:
Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.
Источник
Движение тела брошенного под углом к горизонту
Движение тела, брошенного под углом к горизонту. Полный разбор движения. Вывод формул 
Это движение представляет собой совокупность двух видов движения:
- равномерного движения по оси X (горизонтально): скорость v=const , т.к. ускорение a=0
- равнопеременного по оси Y (вертикально): скорость v=v0+at , т.к. ускорение а=-g
Как же найти скорость?
Сначала найдем скорости по X и по Y отдельно.
- Чтобы найти скорость по оси X, которая будет постоянная на всем пути, определим проекцию V0 на ось X:
Проекция V0 на ось Х – это прилежащий к углу α катит:
Т.к. Vx – постоянна, поэтому:
- Чтобы найти скорость по оси Y, которая будет меняться, определим проекцию V0 на ось Y, это будет начальная скорость по вертикальной оси:
Проекция V0 на ось Y – это противолежащий к углу α катит:
Так как Vy, как мы уже говорили, равнопеременная скорость, то:
Учитывая, что ускорение направлено против вертикальной оси (а=-g), и подставляя V0y получим:
Зная проекции скорости, можем ли мы восстановить саму скорость? (зная катеты треугольника можем ли мы найти гипотенузу?)
Конечно! Теорема Пифагора.
Скорость – дело понятное, как же быть с пройденным путем? Очень просто.
Так как мы сказали, что имеем дело с двумя видами движения в одном, а значит и пути у каждого из видов движения будут разные:
- Горизонтального движение по оси Х равномерное, путь при равномерном движении:
Обозначим путь по Х за Х и подставим нашу скорость вместо V, получим:
- Вертикальное движение по оси Y равнопеременное, путь при равнопеременном движении:
Аналогично, обозначим путь по Y за Y, подставим нашу скорость вместо V0 и ускорение а=-g получим:
ВАЖНО! Часто в задачах встречается ситуация, когда нужно найти высоту подъема или дальность полета .
Высота подъема находится очень просто. Все что нужно для решения большинства задач находится в получившихся уравнениях:
Верхняя точка отличается тем, что в ней происходит изгиб. Происходит этот изгиб из-за ускорения свободного падения. Полная скорость , т.к. она направлена по касательной, становится направленной горизонтально , а значит проекция полной скорости по Y равна нулю:
Запишем концовку предыдущего уравнения и выразим время — время в этой формуле соответствует той же самой верхней точке , назовем его – время подъема (tп) .
Высота подъема – это координата Y, поэтому вставляем tп в уравнение для Y и получаем искомую высоту собственной персоной:
Преобразуем и получим высоту подъема:
Дальность полета – это координата Х в точке падения, поэтому время уже накопится в два раза больше:
Аналогично подставим время в формулу для координаты Х:
Применим формулу из триганометрии: 2sin cos = sin, применим и получим:
Источник
Движение тела, брошенного под углом к горизонту (бросок)
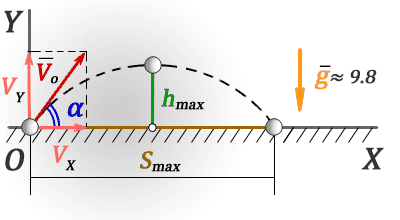
Движение тела, брошенного под углом к горизонту, — движение тела в двумерной системе координат (по двум осям) при изначальном направлении начальной скорости под углом к горизонту. Данное движение является сложным видом механического движения с криволинейной траекторией. Такие типы движений принято рассматривать в проекции на оси выбранной системы координат. В нашем конкретном случае возьмём декартову систему координат и запустим тело под углом к оси ОХ (рис. 1).
Рис. 1. Тело бросили под углом к горизонту
Классическая постановка задач на подобную тематику: тело бросили под углом к горизонту с начальной скоростью , найти различные параметры движения.
Первое, что мы сделаем, это попробуем данное сложное движение представить как сумму простых (рис. 2).
Рис. 2. Тело бросили под углом к горизонту (максимальная высота подъёма, путь по горизонтали, движение)
Рассмотрим само движение. После броска траектория движущегося тела представляет собой параболу (докажем позже). Выберем произвольную точку на параболе и укажем ускорение, с которым движется тело в данный момент (ускорение свободного падения). Направление данного ускорения — вертикально вниз. Проекции данного ускорения на ось ОХ ( (м/ ), а на ось OY ( (м/ ).
Тогда, вдоль оси ОХ, тело движется равномерно (т.к. ускорение вдоль этой оси равно 0). Более сложным является движение тела вдоль оси OY: между точками A и B тело движется замедляясь, при этом движение равнозамедленное. Между точками B и C движение равноускоренное (рис.2, подписи). Исходя из установленного вида движения, можем решать задачу.
Рис. 3. Тело бросили под углом к горизонту (проекции скоростей)
Для рассмотрения движения тела вдоль осей, введём начальные скорости движения тела вдоль выбранных нами осей (рис. 3). На рисунке представлена часть траектории в самом начале движения. Начальные скорости движения вдоль осей обозначим и . Исходя из треугольника, катетами которого являются наши проекции (можно построить параллельным переносом), а гипотенузой — модуль вектора начальной скорости ( ), можем найти значения необходимых нам проекций:
Вернёмся к рисунку 2. Попробуем найти полное время полёта ( ). Для этого воспользуемся тем, что вдоль оси OY тело движется равнозамедленно, а в точке B движение вдоль этой оси и вовсе останавливается. Таким образом, конечная скорость в этой точке вдоль оси OY равна 0. Тогда, исходя из движения:
— т.к. время движения от точки А до B, и от B до C одинаково. Тогда:
Перейдём к вопросу о максимальной дальности броска в горизонтальном направлении ( ).
Вдоль горизонта тело движется равномерно (рис. 2). Тогда путь, проделанный телом за время :
А с учётом (1) и (5):
Перейдём к максимальной высоте полёта ( ). Данный параметр связан с движением тела вдоль оси OY, которое, как мы выяснили, является равноускоренным/равнозамедленным. Рассмотрим участок BC: для него вдоль соответствующей оси тело без начальной скорости движется с ускорением ( ) в течение времени , формируем уравнение:
Таким образом, ряд параметров движения при броске под углом к горизонту можно вычислить, зная лишь начальные параметры броска.
Рис. 4. Тело бросили под углом к горизонту (конечная скорость)
Далее попробуем найти конечную скорость движения (при таких движениях, конечная скорость — скорость при подлёте к Земле). Рассмотрим конечную точку движения С (рис. 4). Скорость тела направлена под неким углом . Построим проекции данного вектора на оси OX и OY. На основании построенного треугольника реализуем теорему Пифагора для поиска модуля полной конечной скорости:
Найдём компоненты вектора . Т.к. движение вдоль оси OX равномерное, значит, , используя (1):
Движение вдоль оси OY от точки B в точку C равноускоренное, причём, без начальной скорости за время , тогда:
Используя (5), получим:
Подставим (12) и (13) в (10):
Для избавления от тригонометрических функций мы воспользовались основным тригонометрическим тождеством. Таким образом, доказано, что конечная скорость такого движения равна начальной, кроме того, из треугольника видно, что тело подлетело к земле под углом .
Вывод:
- для движения тела, брошенного под углом к горизонту, выведены добавочные формулы: (5), (7), (9), которые могут существенно упростить решение задачи.
- представлен один из общих способов нахождения скорости при криволинейном движении (через теорему Пифагора и поиск компонент вектора).
Источник
