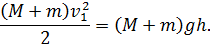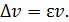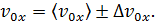ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА
Описание установки и метода измерений

Так как в горизонтальном направлении внешние силы отсутствуют (силой трения мы пренебрегаем), то на основании закона сохранения импульса можно записать
где m – масса пули; 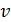

Чтобы определить скорость 
Подставив (2) в (1),найдем выражение для скорости пули:
Из прямоугольного треугольника АКО (рис. 1) имеем
Так как 
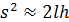
Подставив найденное значение h в выражение (3), получим для скорости пули формулу
Формула (4) является расчетной. Величины s, l определяют экспериментально.
Порядок выполнения работы
1. Масса пули и маятника указаны на установке.
2. Измерить линейкой расстояние l от точки подвеса до точки крепления нити к маятнику.
3. Привести маятник в состояние равновесия и определить положение указателя по шкале.
4. Установить маятник так, чтобы его ось совпадала с осью ствола пистолета и произвести пять выстрелов одной и той же пулей, каждый раз отмечая смещение указателя по шкале. Результаты измерений записать в табл. 1.
5. Вычислить скорость пули по формуле (4), подставив среднее значение смещения 
| Номер опыта | Смещение  , м , м | 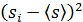 | Масса маят- ника М, кг | Масса пули m, кг | Длина подвеса L, м |
 |  , м , м |  | 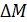 , кг , кг | 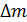 , кг , кг |  , м , м |
6. Вычислить квадрат абсолютной ошибки измерения смещения маятника:
7. Вычислить относительную ошибку измерения скорости:
8. Найти абсолютную ошибку:
9. Результат измерения записать в виде
Контрольные вопросы
1. Что называется импульсом тела?
2. Какая система называется замкнутой или изолированной?
3. Сформулируйте закон сохранения импульса. Какова связь этого закона с законами Ньютона?
4. Какие существуют виды механической энергии?
5. В каких единицах измеряется энергия в системах единиц СИ и СГС?
6. Сформулируйте закон сохранения механической энергии?
7. Какие силы называются потенциальными и непотенциальными?
8. Какова связь законов сохранения энергии и импульса со свойствами пространства и времени?
9. Как найти изменение механической энергии неизолированной диссипативной системы?
10. Какие превращения энергии происходит в данной работе?
11. Выведите расчетную формулу.
ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ
КИНЕМАТИЧЕСКИМ МЕТОДОМ

Выстрел из пружинного пистолета производится в горизонтальном направлении (рис. 2). Движение пули вдоль оси X является равномерным, поэтому дальность полета
где 


Из (1) и (2) следует, что
Формула (3) является расчетной.
Порядок выполнения работы
1. Произвести 5 выстрелов из пистолета, расположенного на столе, в ящик с песком или лист бумаги, расположенный на полу. После каждого выстрела по отметке пули на песке, или на листе, измерить дальность полета S.
2. Измерить высоту h.
3. Результаты измерений S и h записать в табл. 1.
| Номер опыта |  , м , м |  , м 2 , м 2 | h, м |
 |  |  |  , м , м |
4. Вычислить скорость пули 

5. Вычислить квадрат абсолютной ошибки измерения
где 
6. Вычислить относительную погрешность измерения скорости
7. Найти абсолютную погрешность
Результат измерения записать в виде
Сравнивая значения скоростей, найденных с помощью баллистического маятника и кинематическим методом для одного и того же пистолета и пули, убедиться в закономерной взаимосвязи уравнений динамики и кинематики.
Контрольные вопросы
1. Что такое средняя и мгновенная скорость, среднее и мгновенное ускорение, тангенциальное и нормальное ускорение?
2. Получить уравнение траектории пули.
3. Определить скорость и ее направление при приземлении пули.
4. Определить нормальное и тангенциальное ускорение пули при вылете и приземлении.
5. Определить время полета пули
6. Определить радиус кривизны траектории при вылете и приземлении пули.
Библиографический список
1. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 1.1–1.3, 3.2–3.4, 5.1.
2. Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. –§ 2, 3, 9, 12–15.
3. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – § 3–4, 10–24.
4. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Гл.2 § 2.1–2.4. Гл. 3 § 3.1–3.4.
5. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д. В. Сивухин. – М.: Физматлит МФТИ, 2005. – § 1–5, 9–12.
6. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 1.1 § 1.3, 1.4. Гл.1.3 § 1.12–1.15.
Источник
ЛАБОРАТОРНАЯ РАБОТА № 106
Определение скорости полета пули с помощью
баллистического маятника
Цель работы: Определение скорости пули с помощью баллистического маятника с использованием законов сохранения импульса и энергии.
Приборы и принадлежности: баллистический маятник, шкала, пружинный пистолет, линейка и пули.
Теоретическое введение
Из практики известно, что скорость полета пули достигает значительной величины. Поэтому прямое измерение скорости, т.е. определение времени, за которое пуля проходит известное расстояние, требует специальной аппаратуры. Много проще измерять скорость пули косвенными методами, среди которых широко распространены методы, использующие неупругие соударения, т.е. соударения, в результате которых столкнувшиеся тела соединяются вместе и продолжают движение как одно целое.
Пусть летящая пуля испытывает неупругий удар со свободным неподвижным телом значительно большей массы. После удара тело начинает двигаться, причем скорость его во столько раз меньше скорости пули, во сколько раз масса пули меньше массы тела. (Этот результат можно получить с помощью закона сохранения импульса). Если теперь измерить сравнительно небольшую скорость тела, то легко можно вычислить и скорость полета пули.
К числу методов, основанных на этой идее, относится и метод баллистического маятника. В данной работе для определения скорости пули использованы законы сохранения импульса и полной механической энергии.
Описание рабочей установки и метода измерений

Баллистический маятник представляет собой тяжелое тело массой М, подвешенное на двойном бифилярном подвесе (рис.1). Когда после выстрела пуля попадает в это тело, то оно отклоняется от положения равновесия.
Пренебрегая сопротивлением воздуха, к системе «маятник-пуля» можно применить закон сохранения импульса, который в проекции на ось x запишется
где m υ – проекция импульса на ось x до взаимодействия;
(М+ m ) U — проекция импульса системы (пуля +маятник) на ось x неупругого удара.

Закон сохранения импульса: в изолированной системе тел сумма импульсов взаимодействующих тел остается постоянной во времени, т.е. 
Закон сохранения механической энергии: в изолированной системе тел, где действуют только консервативные силы, полная механическая энергия (кинетическая плюс полная потенциальная энергии) остается постоянной, т.е. Е=Ек+Еп= const .
При ударе пули маятник вместе с пулей приобретает кинематическую энергию, равную после соударения
Маятник с пулей приходит в движение, отклоняется на некоторый угол от вертикали, и центр масс системы «маятник-пуля» поднимается на некоторую высоту h (рис.2).
Если пренебречь трением в подвесе маятника и сопротивлением воздуха, то можно рассматривать систему «маятник-пуля» как изолированную, консервативную и применять к ней закон сохранения полной механической энергии.
В момент наибольшего отклонения маятника его кинетическая энергия Ек полностью превратится в потенциальную энергию силы тяжести
где g – ускорение свободного падения тела.
Подставив (5) в (2), найдем выражение для скорости пули
Следовательно, скорость пули можно вычислить, если измерить высоту подъема h центра масс маятника. Однако измерение h довольно сложно. Его можно заменить более простым измерением горизонтального перемещения S, которое определяют по неподвижной шкале.
Если после соударения маятник отклонился на небольшой угол (рис.2), то можно считать, что центр масс маятника перемещается вдоль хорды АВ. Тогда из подобия треугольников АКВ и ОАС можно записать отношение
где ВК = S— горизонтальное смещение маятника; АК = h , ОС ^ АВ .
При малом отклонении S и достаточной длине подвеса l ( S l ) можно положить, что

Тогда соотношение (6) можно записать в виде

Поставив (7) в (5), получим формулу для скорости пули:
Формула (8) является расчетной. Определяя величины M, m , S, l , экспериментально, по формуле (7) можно определить скорость пули υ .
Ход работы
1. Привести маятник в состояние равновесия и подвесить шкалу под указатель маятника.
2. Произвести 5 – 6 выстрелов, каждый раз отмечая смещения указателя по шкале. Результаты измерений записать в таблицу.
3. Вычислить скорость пули по формуле (8).
4. Вычислить абсолютную погрешность измерения S по формуле:
где tp ( n )— коэффициент Стьюдента для доверительной вероятности p = 0,95 и числа измерений n .
5. Вычислить относительную погрешность измерения скорости
6. Найти абсолютную погрешность
7. Результаты измерения записать в виде

Источник