Как вывести формулу герона для треугольника

Формула Герона.

Формула Герона позволяет определить площадь треугольника (S) из его сторон a, b, c.

Чтобы вычислить площадь треугольника ∆ABC, если известны длины его сторон a, b и c, используют формулу Герона:

где p — полупериметр треугольника:

.

Рассмотрим нахождение площади треугольника с помощью формулы Герона:

Есть треугольник со сторонами a = 5, b = 6, c = 7. Вычислим полупериметр:

Далее подставляем данные в формулу для определения площади:

Площадь треугольника, определенная при помощи формулы Герона равняется 14,7 см 2 .

Формула Герона, доказательство.

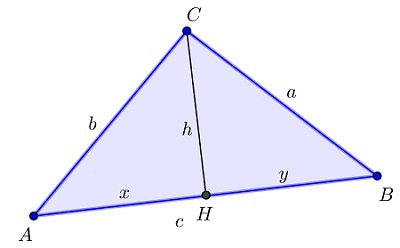
В нем: CH — высота треугольника ABC, которая проведена из вершины C, |CH|=h, |AH|=x, |BH|=y.

Тогда c=x+y, и из теоремы Пифагора из треугольников ACH и BCH имеем:

Учитывая, что x+y=c, получаем и .

Складываем последнее равенство с равенством y+x=c, получаем:

Далее находим высоту h треугольника:

Подставляем эти выражения в определенное выражение для h 2 :

Учитываем то, что , получаем требуемое.

Источник

Формула Герона для треугольника

В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.

Формула площади

Площадь треугольника ( S ) равняется квадратному корню из произведения его полупериметра ( p ) на разности полупериметра и каждой из его сторон ( a, b, c ).

Полупериметр ( p ) вычисляется таким образом:

Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.

Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.

Примеры задач

Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.

Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.

Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
= .

Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.

Решение
Пусть гипотенуза – это c , известный катет – a , а неизвестный – b .

Применим Теорему Пифагора, чтобы найти длину катета b :
b 2 = = = , следовательно,

Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.

Остается только использовать формулу для нахождения площади:
= = .

Источник

Формула Герона для площади треугольника

Треугольник – это фигура, которая образуется после соединения трех точек, не лежащих на одной прямой отрезками. Точки называются вершинами, а отрезки сторонами. Для расчета треугольника существует множество формул, которые помогают найти как длины сторон, радиусы углов и прочие составляющие фигуры, так и площадь треугольника.

Самой распространенной формулой для расчета площади треугольника по трем сторонам является формула Герона . Если известны длины всех сторон, то можно вычислить площадь фигуры, применив формулу Герона для площади треугольника.

где a , b , c – длины сторон, а p – полупериметр.
Полупериметр – это сумма длин всех сторон поделенная на два.

Калькулятор нахождения площади треугольника по формуле Герона

Сторона a=	Сторона b=	Сторона c=
Ответ: Площадь треугольника = 6.000

Три окружности с радиусами 6, 7, 8 внешне попарно касаются друг друга. Найти площадь треугольника, образованного центрами этих окружностей. Посмотреть решение

училась в школе шесть десятков лет назад, геометрию забыла, но в связи с тем, что мебель из ДСП смешно ставить в сантехническую кабину (недолговечна), а из дерева и красивая пока недоступна. На сайтах гостиниц Бахрейна очень понравилась, примерно в похожем стиле хочу сделать сама угловой шкаф в ванную, но чтобы закупить материалы, надо начертить детали и посчитать объем и без геометрии здесь не обойтись. Поэтому я благодарна Вам за теорему Пифагора, за древнеиндийских математиков, за тригонометрические формулы и за калькуляторы расчетов. С искренним уважением Нина Ивановна!

#мыэтонепроходили
Что это за точка на гипотенузе С, которая делит ее на два отрезка С1 и С2 ? Причем произведение С1 на С2 численно равно площади треугольника.

Вбиваем стороны 2,3,5 и вуаля:

Ответ: Площадь треугольника = 0.000

Каждая сторона должна быть меньше суммы двух других. 5>2+3?!

Это не треугольник, это 3 точки на одной прямой

Стороны: 3,4,7 и оппа!
Ответ: Площадь треугольника = 0.000

Потому что у треугольника со сторонами 3, 4 и 7 площадь таки будет 0. 3+4=7. Треугольник вырождается в отрезок.

Нет, по теории, любой треугольник можно назвать таковым, если сумма двух сторон его больше или равна оставшейся стороны.

Например:
стороны 10 25 30, следует что это треугольник так как
(10+25)>30
(10+30)>25
(30+25)>10

Пытался воспользоваться Вашим калькулятором…бесполезно. говорит : такого треугольника нет ……а именно : 3.354 +3.54+12.40.
Может кто-то поможет ?

Ответ: сумма любых 2-х сторон треугольника > 3-й стороны. А у Вас получается 3,…+3,…

Господа, неравенство треугольника ещё никто не отменял. Поэтому, прежде чем вычислять площадь треугольника, проверяют его существование, используя неравенство треугольника.

Источник

Что можно вычислить по формуле Герона

Формула Герона

Формула Герона носит такое название в честь греческого математика и инженера Герона Александрийского. Он жил в I веке нашей эры. Герон занимался механикой, оптикой, геометрией и гидростатикой. Учёный интересовался треугольниками с целочисленными сторонами и целочисленными площадями. Такие фигуры получили название Героновых треугольников.

Формулировка теоремы Герона

Формула Герона – это арифметическая формула для вычисления площади треугольника по длинам его сторон. В таком случае площадь равна корню из произведения разностей полупериметра и каждой из его сторон.

Формула и доказательство

Формула Герона выглядит следующим образом:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

где S – это площадь треугольника; a, b, c – это стороны треугольника; p – это полупериметр треугольника.

Чтобы вычислять полупериметр, нужно пользоваться формулой:

Приведем доказательство.

Для этого рассмотрим треугольник ABC.

CH – высота треугольника.

По теореме Пифагора из треугольников ACH и BCH получаем:

Если сложить последнее равенство с \(y+x=c\) , то получается

Найдем высоту треугольника.

Так как \(p=\frac12\left(a+b+c\right)\) , то \( b+c=2p-a\) , \( a+b=2p-c\) , \(a+c=2p-b\) , \(a+b+c=2p\) .

С помощью этих равенств найдем высоту.

А так как \(S=\frac12ch\) , то теорема доказана.

Для каких треугольников действует теорема

Применение формулы Герона допустимо для треугольников, у которых известны длины всех их сторон.

Примеры решения задач

Задача 1

Рассчитать площадь треугольника, если a=6, b=8, c=6.

Решение

Тогда площадь треугольника равна:

Задача 2

Вычислить площадь параллелограмма, если одна из его сторон равна 51, а диагонали равны 40 и 74.

Решение

Диагонали AC и BD пересекаются в точке O.

Если AD = 51, AC = 40 и BD = 74, то AO = 20, OD = 37.

По формуле Герона:

Ответ: 1224 см 2 .

Задача 3

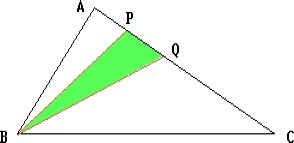
В треугольнике ABC три стороны: AB = 26, BC = 30 и AC = 28. Найти часть площади этого треугольника, заключённую между высотой и биссектрисой, проведёнными из вершины B.

Решение

BP и BQ – высота и биссектриса треугольника.

По формуле Герона:

По свойству биссектрисы треугольника:

Соответственно \(AQ=\frac<13><28>AC = 13\) .

По теореме Пифагора из треугольника APB получаем:

Следовательно, \(PQ = AQ – AP = 13 – 10 = 3\)

Источник

Как найти площадь треугольника

О чем эта статья:

Основные понятия

Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Формула площади треугольника

Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.

Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.

Общая формула

1. Площадь треугольника через две стороны и угол между ними.

S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.

2. Площадь треугольника через основание и высоту.

S = 0,5 * a * h, где a — основание, h — высота.

3. Площадь треугольника через описанную окружность и стороны.

S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны.

S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.

Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:

S = r * p, где p — полупериметр.

5. Площадь треугольника по стороне и двум прилежащим углам.

S = a 2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.

6. Формула Герона для вычисления площади треугольника.

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

S = √ p * (p − a) * (p − b) * (p − c)​, где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2

Для прямоугольного треугольника

Площадь треугольника с углом 90° по двум сторонам.

S = 0,5 * a * b, где a, b — стороны.

Площадь треугольника по гипотенузе и острому углу.

S = 0,25 * c 2 * sin(2α), где c — гипотенуза, α — любой из прилегающих острых углов.

Гипотенузой принято называть сторону, которая лежит напротив прямого угла.

Площадь прямоугольного треугольника по катету и прилежащему углу.

S = 0,5 * a 2 * tg(α), где a — катет, α — прилежащий угол.

Катетом принято называть одну из двух сторон, образующих прямой угол.

Площадь треугольника через гипотенузу и по радиусу вписанной окружности.

S = r * (r + c), где c — гипотенуза, r — радиус вписанной окружности.

Площадь треугольника вписанного в окружность.

Площадь прямого треугольника по формуле Герона.

S = (p − a) * (p − b), где a, b — катеты, p — полупериметр, который рассчитывается по формуле p = (a + b + c) : 2.

Для равнобедренного треугольника

Поиск площади через основание и сторону.

S = b : 4 * √ 4 * a 2 − b 2 , где a — боковая сторона, b — основание.

Вычисление площади через основание и угол.

S = 0,5 * a * b * sin(α), где a — боковая сторона, b — основание, α — угол между основанием и стороной.

Вычисление площади через основание и высоту.

S = 0,5 * b * h, где b — основание, h — высота, проведенная к основанию.

Поиск площади через боковые стороны и угол между ними.

S = 0,5 * a 2 * sin(α), где a — боковая сторона, α — угол между боковыми сторонами.

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами.

S = b 2 : (4 * tgα/2), где b — основание, α — угол между боковыми сторонами.

Площадь равностороннего треугольника через радиус описанной окружности.

S = (3 * √ 3 * R 2 ) : 4, где R — радиус описанной окружности.

Площадь равностороннего треугольника через радиус вписанной окружности.

S = 3 * √ 3 * r 2 , где r — радиус вписанной окружности.

Площадь равностороннего треугольника через сторону.

S = (√ 3 * a 2 ) : 4, где a — сторона.

Площадь равностороннего треугольника через высоту.

S = h 2 : √ 3, где h — высота.

Таблица формул нахождения площади треугольника

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник