E = mc²: Самое знаменитое уравнение Эйнштейна
Это гораздо больше, чем взаимосвязь массы-энергии, это ключ к пониманию квантовой Вселенной.
В течение сотен лет существовал непреложный закон физики, который никогда не оспаривался: при любой реакции, происходящей во Вселенной, масса вещества сохранялась. Независимо от того, что с чем реагирует, масса исходных веществ и масса получившихся будет равна. Но, по законам специальной теории относительности, масса просто не может быть конечной сохраненной величиной, так как разные наблюдатели не соглашались бы с тем, что такое энергия системы. Вместо этого Эйнштейн смог получить закон, который мы используем сегодня, управляемый одним из самых простых, но самых мощных и изящных уравнений из всех существующих:
В самом известном уравнении Эйнштейна есть только три составляющих:
- E, или энергия, которая является полнотой одной части уравнения и представляет собой полную энергию системы.
- m или масса, которая связана с энергией по коэффициенту пересчета.
- и c², которая является скоростью света в квадрате: эквивалентный коэффициент, уравнивающий массу и энергию.
Это уравнение полностью меняет мир. Как выразился сам Эйнштейн:
Из специальной теории относительности следует, что масса и энергия — это одновременно разные проявления одного и того же — несколько необычная концепция для среднего ума.
Вот три самых важных по значимости вывода, которые следуют из этого простого уравнения:
- Даже массы в покое имеют присущую им энергию. Вы знаете обо всех типах энергий, включая механическую, химическую и электрическую энергию, а также кинетическую энергию. Это все энергии, присущие движущимся или реагирующим объектам, и эти формы энергии могут быть использованы для работы, такой как вращение двигателя, свет лампочки или измельчение зерна в муку. Но даже простая, обычная масса в покое имеет присущую ей энергию: огромное количество энергии. Это несет в себе потрясающий вывод: гравитация, которая существует между любыми двумя массами во Вселенной, также должна работать на основе энергии, которая эквивалентна массе через уравнение E=mc².
- Масса может быть преобразована в чистую энергию. Это второе значение уравнения, где E=mc² точно показывает, сколько энергии вы получаете от преобразования массы. На каждый 1 килограмм массы превращающейся в энергию, мы получим 9×10¹⁶ джоулей энергии, что эквивалентно 21 мегатонн в тротилловом эквиваленте. Когда происходит радиоактивный распад или ядерная реакцию деления или синтеза, начальная масса больше конечной массы — закон сохранения массы не работает. Но разница в количестве масс — это высвобожденная энергия! Это верно для всех ядерных реакций, от распада урана при взрыве атомной бомбы до ядерного синтеза на Солнце и аннигиляции антиматерии. Количество уменьшающейся массы становится энергией, которая рассчитывается из уравнения E=mc².
- Энергию можно использовать для того чтобы сделать массу из ничего… за исключением чистой энергии. Последнее является наиболее глубоким. Если взять два бильярдных шара и столкнуть их друг с другом, вы получите те же два бильярдных шара. Если взять фотон и электрон и столкнуть их вместе, вы также получите фотон и электрон. Но если столкнуть их с достаточным количеством энергии, то получится и фотон, и электрон, и новая материя — пара частиц антивещества. Другими словами, вы создали две новые массивные частицы:
— частицы материи, такие как электрон, протон, нейтрон и т.п.
— и частицы антивещества, такие как позитрон, антипротон, антинейтрон и т.п.,
чье существование может возникнуть, только если будет достаточно энергии. Именно таким образом ускорители частиц, как Большой адронный коллайдер в CERN, ищут новые, нестабильные, высокоэнергетические частицы (например, бозон Хиггса или верхний кварк) — создавая эти новые частицы из чистой энергии. Получаемая масса исходит из имеющейся энергии: m=E/c².
Факт эквивалентности массы-энергии привел Эйнштейна к его величайшему достижению: Общей теории относительности. Представьте, что у вас есть частица материи и частица антивещества, каждая из которых имеет одинаковую массу покоя. Вы можете уничтожить их, и они будут производить фотоны определенного количества энергии, точного количества, заданного формулой E=mc². Теперь представьте, что пара частиц/античастиц движется очень быстро, как будто они падают из космоса, а затем самоуничтожаются вблизи поверхности Земли. Эти фотоны теперь будут иметь дополнительную энергию: не только E от E = mc², но и дополнительную E от количества кинетической энергии, которую они получили при падении.
Если мы хотим сохранить энергию, мы должны понять, что гравитационное красное смещение (а также синее смещение) должно быть реальным. Теория всемирного тяготения Ньютона не может объяснить этого, но в Общей теории относительности Эйнштейна кривизна пространства означает, что попадание в гравитационное поле заставляет вас получать энергию, а выход из гравитационного поля заставляет вас терять энергию. Тогда полное и общее отношение для любого движущегося объекта — это не только E=mc², но и E²=m²c⁴+ p²c² (где p — импульс.) Только обобщая вещи, включающие энергию, импульс и гравитацию, мы можем действительно описать Вселенную.
Великое уравнение Эйнштейна, E=mc², является триумфом мощи и простоты фундаментальной физики. Материя имеет присущее ей количество энергии, масса может быть преобразована (при правильных условиях) в чистую энергию, а энергия может быть использована для создания массивных объектов, которые ранее не существовали. Размышления об этом позволили ученым обнаружить фундаментальные частицы, составляющие нашу Вселенную, изобрести ядерную энергию и ядерное оружие, и открыть теорию гравитации, описывающую, как взаимодействует каждый объект во Вселенной.
Источник
Спросите Итана: по какой фундаментальной причине E = mc²?
Альберт Эйнштейн в 1920 году. Хотя он и совершил множество прорывов в физике, от специальной и общей теорий относительности до фотоэлектрического эффекта и статистической механики, многие задачи он решить не сумел. Самым его знаменитым уравнением остаётся E = mc².
Спросите любого человека, даже не разбирающегося в науке, о достижениях Эйнштейна, и вам приведут в пример самое его знаменитое уравнение: E = mc². Проще говоря, оно означает, что энергия равняется массе, перемноженной с квадратом скорости света. И это очень многое говорит о нашей Вселенной. Единственное уравнение говорит о том, сколько энергии содержится в массивной частице в состоянии покоя, и сколько энергии требуется для создания частиц и античастиц. Оно говорит нам о том, сколько энергии высвобождается в ядерных реакциях, и сколько энергии порождает аннигиляция материи с антиматерией.
Но почему? Почему энергия равняется массе, перемноженной с квадратом скорости света? Почему не как-то иначе? Об этом спрашивает наш читатель:
Уравнение Эйнштейна потрясающе элегантное. Но реальна ли его простота, или же только кажется? Выводится ли оно напрямую из эквивалентности энергии любой массы и квадрата скорости света (а это вообще кажется удивительным совпадением)? Или оно существует только потому, что его члены определены удобным способом?
Отличный вопрос. Давайте исследуем самое знаменитое уравнение Эйнштейна, и посмотрим, почему оно не могло быть другим.

Подготовка к испытаниям ракеты с ядерным двигателем, 1967. Она работает на преобразовании массы в энергию, в основе которого лежит знаменитое уравнение E = mc².
Для начала нужно кое-что понять касательно энергии. Её очень сложно определить, особенно далёкому от физики человеку. Навскидку мы можем придумать несколько примеров.
- Существует потенциальная энергия, т.е. некая форма сохранённой энергии, которую можно освободить. Например, бывает гравитационная потенциальная энергия, когда мы поднимаем массу на большую высоту. Химическая потенциальная энергия, хранящаяся в таких молекулах, как сахара, и способная производить окисление. Электрическая потенциальная энергия, когда накопленный в аккумуляторе или конденсаторе заряд можно разрядить, высвобождая её.
- Существует кинетическая энергия, присущая движущимся объектам.
- Существует электрическая энергия – кинетическая энергия, присущая движущимся зарядам и электрическим токам.
- И ядерная энергия, или энергия, высвобождаемая переходами атомов в более стабильные состояния.
И, конечно же, множество других типов. Энергия – это одна из тех вещей, которые «мы узнаем, когда увидим». Но физикам требуется более универсальное определение. Одно из лучших такое: извлечённая или извлекаемая энергия – это количественная оценка нашей способности произвести работу.
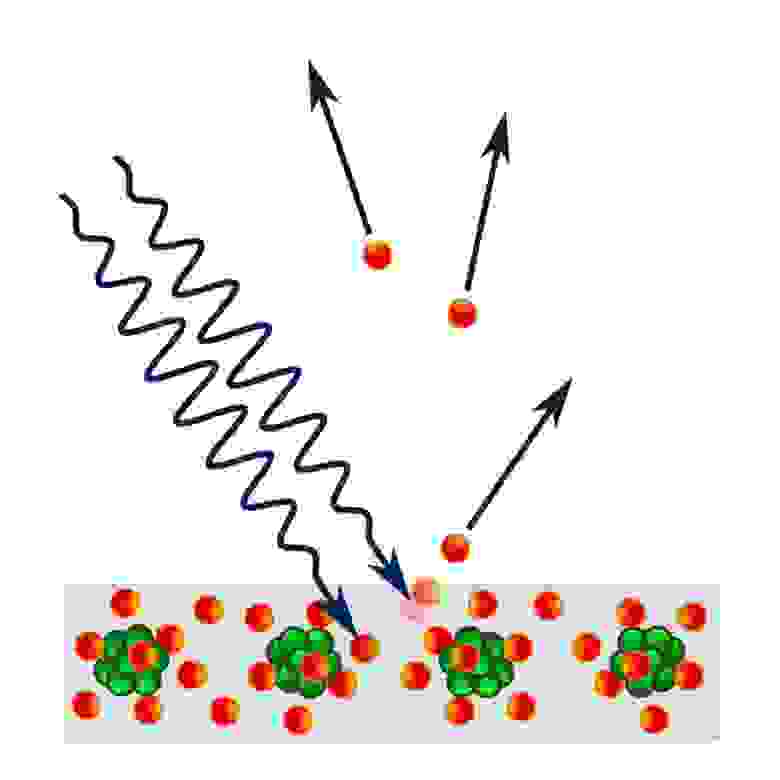
Фотоэлектрический эффект описывает ионизацию электронов фотонами в зависимости от длин волн отдельных фотонов, а не от интенсивности света, суммарной энергии или какого-либо ещё свойства. Если у кванта света достаточно энергии, он может взаимодействовать с электроном, ионизировав его, выбив его из материала, что даст сигнал, который можно обнаружить. Такие фотоны переносят энергию и выполняют работу над ударяемыми ими электронами.
У работы есть своё физическое определение: это сила, прикладываемая в направлении, совпадающем с направлением движения предмета, умноженная на расстояние его перемещения. Поднятие штанги на определённую высоту требует провести работу против силы гравитации, и увеличивает гравитационную потенциальную энергию. Отпустив штангу, мы преобразуем её гравитационную потенциальную энергию в кинетическую. Ударяющая пол штанга преобразует кинетическую энергию в комбинацию из тепловой, механической и звуковой энергии. Энергия в этих процессах не создаётся и не уничтожается, а преобразуется из одной формы в другую.
Большинство людей размышляют о формуле E = mc² в терминах анализа размерностей. Они говорят: так, энергия измеряется в Джоулях, а Джоуль – это килограмм на метр в квадрате на секунду в квадрате. Поэтому, чтобы превратить массу в энергию, нужно умножить это на метр в квадрате, делённый на секунду в квадрате. При этом у нас есть фундаментальная константа с размерностью метр/секунда. Эти рассуждения разумны, но не достаточны.

Фотографии с «Тринити», первого в мире испытания технологии ядерного оружия. Показана ситуация спустя 16, 25, 53 и 100 мс после зажигания. Самая высокая температура достигается в самом начале взрыва, до того, как его объём многократно вырастает.
Ведь вы можете измерять любую скорость в метрах в секунду, а не только скорость света. Кроме того, природе никто не запрещает выдать пропорциональную константу – какой-нибудь множитель типа ½, ¾, 2π, и т.п., чтобы сделать уравнение верным. Чтобы понять, почему уравнение должно выглядеть, как E = mc², и почему других вариантов быть не может, нам надо представить физическую ситуацию, в которой можно будет различить разные интерпретации. Такой теоретический инструмент известен, как «мысленный эксперимент» (или gedankenexperiment, как сказал бы Эйнштейн), и стал одной из великих идей, появившихся в голове Эйнштейна и укоренившихся в научном мейнстриме.
Мы можем представить, что у частицы есть энергия, присущая её массе покоя, и энергия её движения – кинетическая. Можно представить, что частица начала свой путь, находясь высоко в гравитационном поле, то есть с большим запасом потенциальной энергии, но изначально не двигалась. Если мы её уроним, потенциальная энергия превратится в кинетическую, а энергия массы покоя останется той же. Перед самым ударом о землю никакой потенциальной энергии у неё не останется – только кинетическая и энергия массы покоя, какие бы они ни были.
У обозначенной оранжевым частицы, покоящейся над поверхностью земли, не будет кинетической энергии, но будет большой запас потенциальной. Если её отправить в свободное падение, она приобретёт кинетическую энергию, в которую превратится потенциальная.
Теперь добавим ещё одну идею: что у всех частиц есть двойники-античастицы, и что когда они сталкиваются друг с другом, то аннигилируют, выделяя чистую энергию.
Да, E = mc² описывает взаимоотношение массы и энергии, включая количество энергии, необходимое для создания из ничего пар частица-античастица, и то, сколько энергии вы получите, когда такая пара аннигилирует. Но мы пока этого не знаем, мы хотим это доказать!
Давайте представим, что у нас не одна частица находится высоко в гравитационном поле, а сразу и частица, и античастица, и они готовы упасть. Рассмотрим два разных сценария развития, и изучим их последствия.
Появление пар частица-античастица (слева) из чистой энергии – реакция полностью обратимая (справа), они могут аннигилировать, превратившись в энергию. Но для многих систем частиц обратимость не гарантирована.
Сценарий 1: частица и античастица падают, и аннигилируют прямо перед ударом о землю. Ситуация похожа на описанную ранее, просто мы её удвоили. И частица, и античастица начинали с некоего количества энергии массы покоя. Мы не знаем, сколько её было, просто знаем, что у частицы и античастицы они одинаковые, поскольку массы частиц идентичны массам соответствующих античастиц.
Теперь они обе падают, превращая потенциальную гравитационную энергию в кинетическую, в дополнение к их энергии массы покоя. Как и в предыдущем случае, перед ударом о землю вся их энергия заключена в двух видах – энергии массы покоя и кинетической. Только теперь перед самым столкновением они аннигилируют, превращаясь в два фотона, общая энергия которых должна равняться сумме энергий массы покоя и кинетических энергий обеих частиц.
Однако для фотона, массы не имеющего, энергия описывается одним только импульсом, помноженным на скорость света: E = pc. Какой бы ни была энергия обеих частиц перед столкновением с землёй, энергия этих фотонов должна в сумме давать сумму энергий частиц.
Если пара частица-античастица аннигилирует в чистую энергию (два фотона), имея в запасе много гравитационной потенциальной энергии, то в энергию фотона перейдёт только масса покоя (оранжевый). Если уронить эти частицы вниз, чтобы они аннигилировали непосредственно перед ударом, у них будет больше энергии, что приведёт к появлению более синих фотонов.
Сценарий 2: частица и античастица аннигилируют в чистую энергию, а потом падают вниз до земли в виде фотонов с нулевой массой покоя. Тогда вся их энергия массы покоя превратится в энергию фотонов.
Получается, что в данном случае общая энергия этих фотонов, у каждого из которых есть энергия E = pc, должна быть равной сумме энергий масс покоя частицы и античастицы.
Теперь представим, что эти фотоны добрались до поверхности планеты, и после этого мы измеряем их энергию. По закону сохранения, их энергия должна равняться энергии фотонов из первого сценария. Значит, фотон должен набирать энергию, падая в гравитационном поле. Это явление известно, как гравитационный синий сдвиг. Кроме того, из этого следует идея о том, что масса покоя частицы должна равняться E = mc².
Когда квант излучения покидает гравитационное поле, его частота должна испытать красный сдвиг, чтобы энергия сохранилась. При падении частота должна сдвинуться в синий диапазон. Это имеет смысл, только если гравитация связана не только с массой, но и с энергией. Гравитационное красное смещение – одно из ключевых предсказаний Общей теории относительности Эйнштейна. Но его только недавно проверили в окружении с такими сильными полями, как центр нашей Галактики.
Есть только одно определение энергии, подходящее ко всем частицам, и имеющим, и не имеющим массу, и удовлетворяющее сценариям 1 и 2, которые должны выдать одинаковые результаты. E = √(m 2 c 4 + p 2 c 2 ). Посмотрим, что с ним будет в разных ситуациях.
- У массивной частицы в состоянии покоя и без импульса энергия будет равной √(m 2 c 4 ), то есть, E = mc².
- Безмассовая частица обязана двигаться, а её масса покоя равна нулю. Её энергия равняется √(p²c²), или E = pc.
- У массивной частицы, движущейся значительно медленнее скорости света, импульс можно записать как p = mv, и тогда её энергия становится равной √(m²c 4 + m²v²c²). Это можно переписать как E = mc² * √(1 + v²/c²), если v значительно меньше c.
Если вам незнаком последний член, не расстраивайтесь. Если v очень мало по сравнению с c, вы можете выполнить разложение в ряд Тейлора, и получите E = mc² • [1 + ½(v²/c²) + . ]. Взяв первые два члена, вы получите E = mc² + ½mv²: массу покоя плюс старую добрую, нерелятивистскую формулу кинетической энергии.
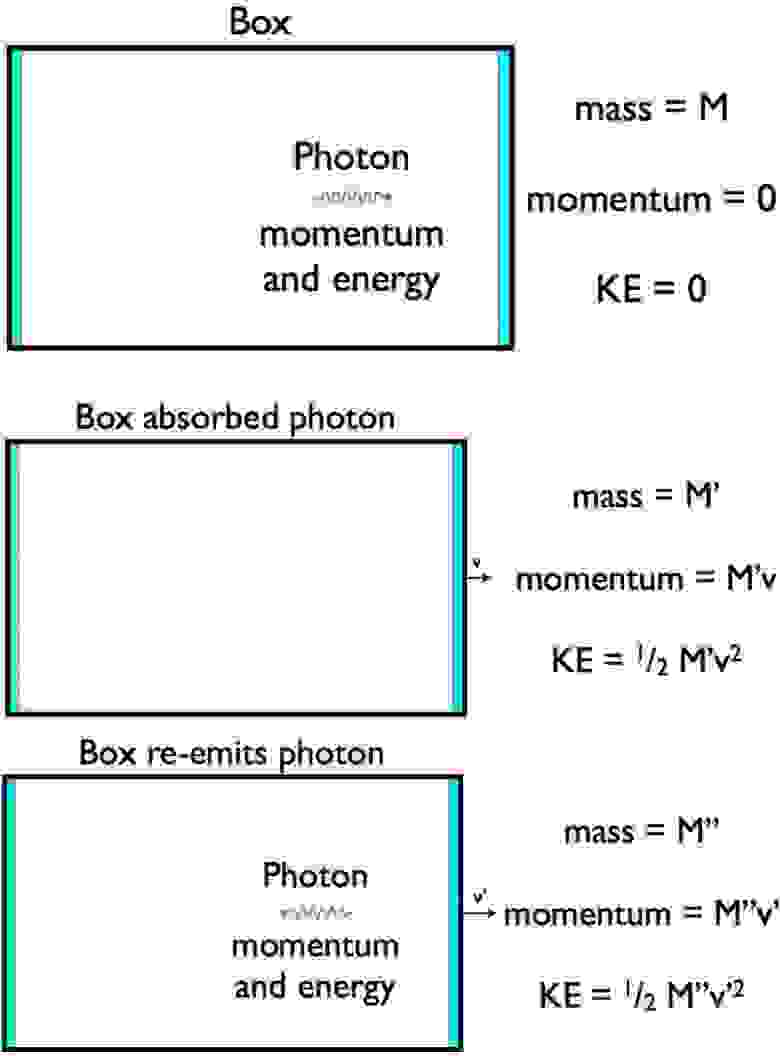
Вверху: фотон движется внутри коробки. В середине: коробка поглотила фотон. Внизу: фотон переиспущен в противоположном направлении. Из такого эксперимента, принимая законы сохранения энергии и импульса, можно вывести знаменитое E = mc².
Конечно, так выводить E = mc² не стоит, но это мой любимый способ иллюстрации этой задачи. Могу порекомендовать ещё три способа иллюстрации, а также описание того, как это сделал сам Эйнштейн. Второй моей любимой иллюстрацией вывода этой формулы будет рассмотрение фотона, движущегося в неподвижной коробке с зеркалом на одной из стенок.
Когда фотон сталкивается с зеркалом, он на некоторое время поглощается, в результате чего коробка должна приобрести немного энергии, и начать двигаться в том же направлении, что и фотон – это единственный способ сохранить энергию и импульс.
После переиспускания фотон движется в противоположном направлении, поэтому коробке (потерявшей немного массы после переиспускания фотона) нужно двигаться вперёд ещё быстрее.
И хотя тут много неизвестных, в такой ситуации можно написать множество уравнений, которым необходимо совпадать. Общая энергия всех частей системы и общий момент должны быть эквивалентными. Если решить эти уравнения, получится только одно определение энергии массы покоя: E = mc².
Эйнштейн выводит Специальную теорию относительности перед зрителями, 1934 год. Если потребовать сохранения энергии и применить теорию относительности к подходящим системам, необходимо, чтобы E = mc².
Можно представить себе совсем не такую вселенную, в которой мы живём. Возможно, там не сохраняется энергия – и тогда формула E = mc² может не быть универсальным выражением массы покоя. Возможно, мы могли бы нарушить закон сохранения импульса – тогда наше определение общей энергии, E = √(m 2 c 4 + p 2 c 2 ), не было бы верным. А если бы там не действовала Общая теория относительности, или импульс и энергия фотона не были бы связаны соотношением E = pc, тогда E = mc² не была бы универсальной формулой для массивных частиц.
Но в нашей Вселенной энергия сохраняется, и работает Общая теория относительности. Поэтому нужно просто подобрать подходящие условия эксперимента. И даже не проводя его на самом деле, можно прийти только к одному непротиворечивому значению для энергии массы покоя частицы. Можно представить себе вселенную, в которой взаимоотношение массы и энергии были бы другими, но она была бы совсем непохожей на нашу. И это не просто удобное определение – это единственный способ сохранить энергию и импульс с имеющимися у нас законами физики.
Источник