Определение момента инерции маятника Максвелла. Определение силы натяжения нитей при движении и в момент «Рывка» (нижняя точка траектории)
Страницы работы
Содержание работы
1. Цель работы: определение момента инерции маятника Максвелла. Определение силы натяжения нитей при движении и в момент «рывка» (нижняя точка траектории).
2. Теоретические основы работы.
При движении маятника Максвелла происходит процесс перехода потенциальной энергии в кинетическую и обратно. Разумеется, механическая энергия постепенно убывает в результате действия сил трения. Согласно теореме о движении центра масс, центр масс движется как материальная точка, масса которой равна массе системы, а действующая на нее сила — геометрической сумме всех внешних сил, действующих на систему:
Здесь индекс С означает центр масс системы.
Основное уравнение динамики вращательного движения для маятника максвелла относительно мгновенной оси O‘Z, проходящей через центр масс имеет вид
Здесь JZ — момент инерции маятника относительно оси O‘Z.
ЕZ — проекция углового ускорения на ось O’Z; левая часть уравнения — алгебраическая сумма моментов внешних сил относительно оси O’Z.
Если нить не проскальзывает, то скорость центра масс маятника и угловая скорость w связаны кинематическим соотношением
а) Определение момента инерции маятника Максвелла.
Используя закон сохранения механической энергии можно экспериментально определить момент инерции маятника. Для этого измеряется время t опускания маятника массой m с высоты h.
Примем потенциальную энергию маятника Максвелла Wп.н. = 0 в положении, когда маятник находится в нижней точке. Кинетическая энергия в этом положении
Здесь V — скорость центра масс маятника; w — угловая скорость;
J — момент инерции маятника относительно оси, проходящей через центр масс: m = mв + mд + mл — масса маятника; mв, mд,mл — массы вала, диска и кольца, входящих в состав маятника. В верхнем положении маятника его потенциальная энергия
а кинетическая энергия равна нулю. Из закона сохранения механической энергии для маятника Максвелла (диссипативными силами, т.е. силами трения, сопротивления воздуха и т.п. пренебрегаем) следует
Так как центр масс маятника движется прямолинейно и равноускоренно, то
Подставляя соотношение (4) в (2) и используя соотношение между скоростью центра масс и угловой скоростью вращения маятника относительно оси симметрии, получим формулу для расчета экспериментального момента инерции маятника Максвелла
Здесь r – радиус вала
Полученный результат сравниваем со значением момента инерции, определяемым из теоретических соображений. Теоретический момент инерции маятника Максвелла можно рассчитать по Формуле
Здесь JB, JД, JK — моменты инерции составных частей маятника: вала, диска и кольца соответственно. Используя общую формулу для определения момента инерции
найдем моменты инерции элементов маятника Максвелла.
Момент инерции вала JB = mвr2/2 (8)
Момент инерции диска
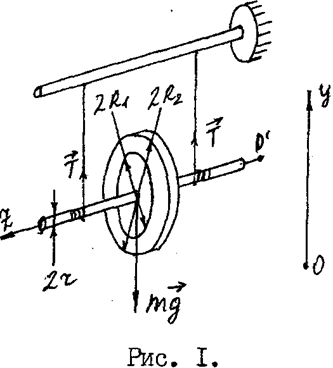
Здесь R1 — радиус диска, он же внутренний диаметр кольца (рис. 1). Момент инерции кольца
Здесь R2 — внешний диаметр кольца
б) Определение силы натяжения нитей при движении маятника Максвелла ТД и в момент «рывка» – ТР.
Движение маятника Максвелла описывается системой уравнений
Из (11) и (12) следует, что при движении маятника Максвелла сила натяжения нити равна
где момент инерции маятника J определяется соотношением (5).
Источник
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛА



Нетрудно показать, что любое движения твердого тела (например, движение космонавта на тренировочных центрифугах и т.д.) может быть представлено как наложение двух простых видов движения: поступательного и вращательного.
При поступательном движении все точки тела получают за одинаковые промежутки времени равные по величине и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми.
При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.
Представляет интерес сопоставление основных величин и формул механики вращающегося твердого тела и поступательного движения материальной точки. Для удобства такого сопоставления в таблице 1 слева приведены величины и основные соотношения для поступательного движения, а справа – аналогичные для вращательного движения.
Таблица 1
| Поступательное движение | Вращательное движение |
S – путь 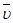 – линейная скорость – линейная скорость 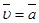 – линейное ускорение m – масса тела – линейное ускорение m – масса тела 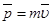 – импульс тела – импульс тела 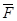 – сила Основной закон динамики: – сила Основной закон динамики: 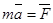 Кинетическая энергия: Кинетическая энергия: 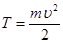 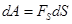 – работа – работа | 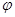 – поворот – поворот 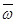 – угловая скорость – угловая скорость 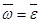 – угловое ускорение J – момент инерции – угловое ускорение J – момент инерции 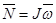 – момент импульса – момент импульса 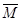 – момент силы Основной закон динамики: – момент силы Основной закон динамики: 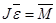 Кинетическая энергия: Кинетическая энергия: 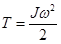 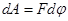 – работа – работа |
Из таблицы видно, что переход в соотношениях от поступательного движения к вращательному осуществляется заменой скорости – на угловую скорость, ускорения – на угловое ускорение и т.д.
В данной работе рассматривается плоское движение, т.е. такое, при котором под действием внешних сил все точки тела перемещаются в параллельных плоскостях. Примером плоского движения может служить качение цилиндра по плоскости.
Это движение можно представить как сумму двух движений – поступательного со скоростью 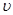
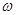
Назвав систему отсчета, относительного которой мы рассматриваем сложное движение твердого тела, неподвижной, движение тела можно представить как вращение с угловой скоростью 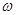
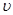
Таким образом, ускорение каждой точки тела складывается из ускорения поступательного движения и ускорения при вращении вокруг оси, проходящей через центр масс. Ускорение поступательного движения 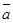
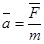 | (4.1) |
где 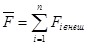
Направление ускорения совпадает с направлением результирующей 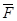
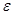
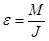 | (4.2) |
где 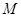
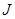
В данной работе плоское движение тела изучается на примере движения маятника Максвелла.
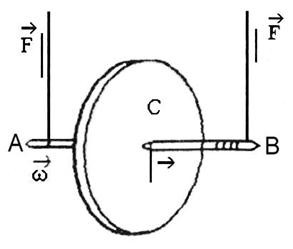
Маятник Максвелла состоит из плоского металлического стержня – оси AB с симметрично закреплены на нем диском С (рис. 1). К концам оси прикреплены две нити, предварительно намотанные на ось. Противоположные концы нитей закреплены на верхнем кронштейне. Диск опускается под действием силы тяжести на нитях, которые разматываются до полной длины. Диск, продолжая вращательное движение в том же направлении, наматывает нити на ось, вследствие чего он поднимается вверх, замедляя при этом свое вращение. Дойдя до верхней точки, диск опять будет опускаться вниз и т.д. Диск будет совершать колебания вверх и вниз, поэтому такое устройство и называют маятником. Суть работы заключается в измерении момента инерции маятника и сравнение полученных результатов с теоретически рассчитанными по известным формулам.
Составим уравнение поступательного движения маятника без учета сил трения о воздух (см. рис. 1)
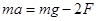 | (4.3) |
где 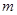
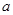
g – ускорение свободного падения;
F – сила натяжения нити.
Уравнение вращательного движения для маятника имеет следующий вид:

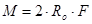 | (4.4) |
где 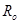
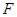
Поступательное и вращательное ускорения связаны соотношением
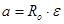 | (4.5) |
Поступательное ускорение маятника можно определить, измерив время опускания маятника t и расстояние, которое он проходит за это время h:
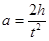 | (4.6) |
Из уравнений (4.3), (4.4), (4.5) и (4.6) выразим момент инерции маятника Максвелла:
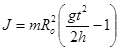 | (4.7) |
Теоретическое значение момента инерции маятника определяют по формуле:
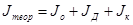 | (4.8) |
где 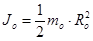
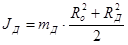
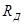
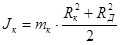
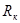
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
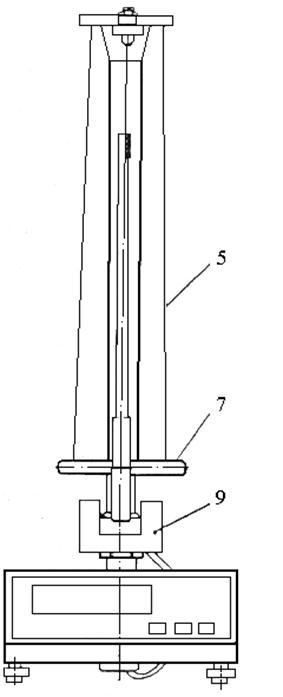
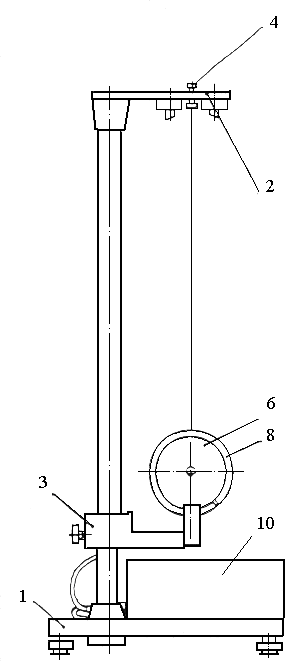
Общий вид установки представлен на рис. 2.
На вертикальной стойке основания 1 крепятся два кронштейна: верхний 2 и нижний 3. Верхний кронштейн снабжен электромагнитами и устройством 4 для крепления и регулировки бифилярного подвеса 5. Маятник представляет собой диск 6, закрепленный на оси 7, подвешенной на бифилярном подвесе. На диск крепятся сменные кольца 8. Маятник со сменными кольцами фиксируется в верхнем исходном положении с помощью электромагнита.
На вертикальной стойке нанесена миллиметровая шкала, по которой определяется ход маятника.
Датчик фотоэлектрический 9 представляет собой отдельную сборку, закрепленную с помощью кронштейна 3 в нижней части вертикальной стойки. Кронштейн обеспечивает возможность перемещения фотодатчика вдоль вертикальной стойки и его фиксирования в любом положении в пределах шкалы 0 – 420 мм.
Фотодатчик 9 предназначен для выдачи электрических сигналов на миллисекундомер физический 10. Миллисекундомер выполнен самостоятельным прибором с цифровой индикацией времени. Он жестко закреплен на основании 1.
 |  |
МЕТОДИКА ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ
Задание 1 . Определить параметры маятника Максвелла.
1. Нарисовать табл. 1.
Таблица 1
| Ось маятника | Диск маятника | Кольца | |||||
| № | Ro, м | Lo, м | RД, м | LД, м | Rк1, м | Rк2, м | Rк3, м |
| Средние значения | |||||||
| Vo = | mo = | VД = | mД = |
2. С помощью штангенциркуля измерить R и L, рассчитать объемы оси и диска Vo иVД.
3. Используя табличные значения плотности металла (алюминия), из которого изготовлены ось и диск, рассчитать значения масс mo иmД. Полученные результаты занести в табл. 1.
4. Измерить штангенциркулем значения Rк (для трех колец) и занести в табл. 1. Определить средние значения.
Задание 2 . Определить момент инерции маятника
1. Нарисовать табл. 2.
2. По шкале, пользуясь указателем кронштейна 3, определить ход маятника h.
| mк1 = кг; | h = м; |
| t, с | tср, с |
| mк2 = кг; | |
| t, с | tср, с |
| mк3 = кг; | |
| t, с | tср, с |
3. Нажать кнопку «Сеть», расположенную на лицевой панели миллисекундомера, при этом должны загореться лампочка фотодатчика и цифровые индикаторы миллисекундомера.
4. Вращая маятник зафиксировать его в верхнем положении при помощи электромагнита, при этом необходимо следить за тем, чтобы нить наматывалась на ось виток к витку.
5. Нажать на кнопку «Сброс» для того, чтобы убедиться, что на индикаторах устанавливаются нули.
6. При нажатии кнопки «Пуск» на миллисекундомере, электромагнит должен обесточится, маятник должен начать раскручиваться, миллисекундомер должен произвести отсчет времени, а в момент пересечения маятником оптической оси фотодатчика счет времени должен прекратиться.
7. Испытания по пунктам 4 – 6 провести не менее пяти раз и определить среднее значение времени t.
8. Определить момент инерции маятника по формуле (4.7).
9. Испытания по пунктам 4 – 6 провести для трех сменных колец.
10. Все полученные результаты занести в таблицу. Определить средние значения.
11. Рассчитать погрешность измеренных значений J.
12. Сравнить теоретические значения момента инерции маятника (4.8) с опытными значениями.
Контрольные вопросы
1. Что называется плоскопараллельным движением?
2. Из каких двух движений складывается сложное движение маятника? Опишите их.
3. Докажите, что маятник совершает движение с постоянным ускорением центра масс.
4. Дайте определение момента инерции. Запишите выражение момента инерции диска, кольца.
5. Сформулируйте закон сохранения механической энергии. Запишите его в применении к маятнику Максвелла.
Источник