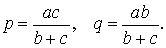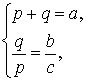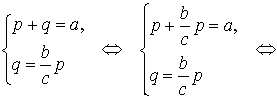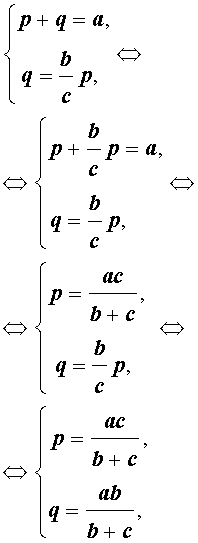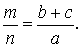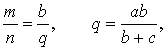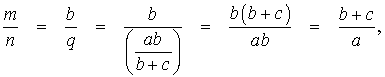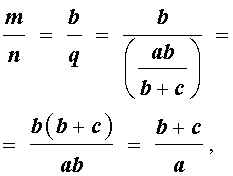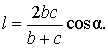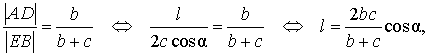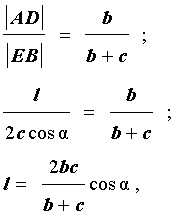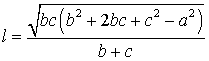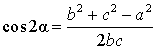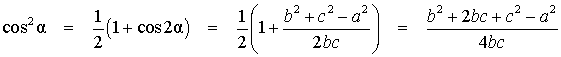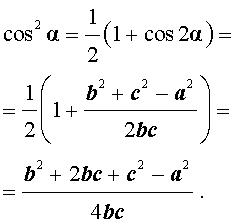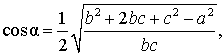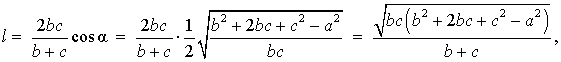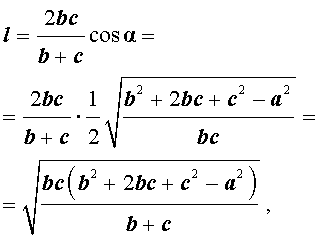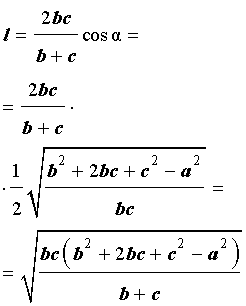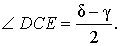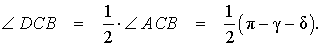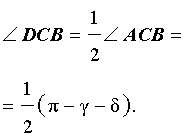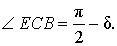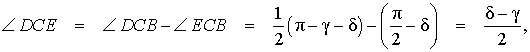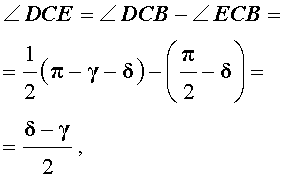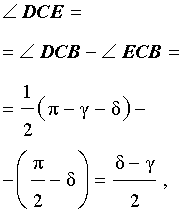Биссектриса треугольника
Напомним, что биссектрисой угла называют луч, делящий угол пополам.
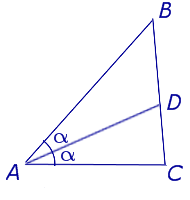
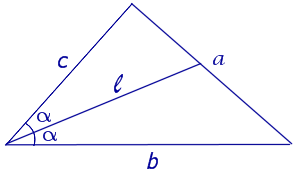
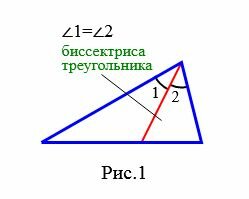
Определение . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника и соединяющий вершину треугольника с точкой на противоположной стороне (рис 1).
Поскольку в каждом треугольнике имеются три угла, то в каждом треугольнике можно провести три биссектрисы.
На рисунке 1 биссектрисой является отрезок AD .
Теорема 1 . Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
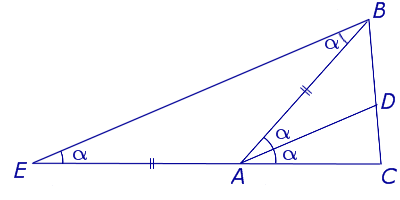
Доказательство . Продолжим сторону AC треугольника ABC , изображенного на рисунке 1, за точку A . Проведем через точку B прямую, параллельную биссектрисе AD . Обозначим точку пересечения построенных прямых буквой E (рис. 2).
Докажем, что отрезки AB и AE равны. Для этого заметим, что угол EBA равен углу BAD , поскольку эти углы являются внутренними накрест лежащими при параллельных прямых EB и AD . Заметим также, что угол BEA равен углу DAC , поскольку эти углы являются соответственными при параллельных прямых EB и AD . Таким образом, угол EBA равен углу BEA , откуда вытекает, что треугольник EAB является равнобедренным, и отрезки AB и AE равны.
Отсюда, воспользовавшись теоремой Фалеса, получаем:
что и требовалось доказать.
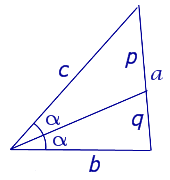
Следствие 1 . Рассмотрим рисунок 3, на котором изображен тот же треугольник, как и на рисунке 1, но для длин отрезков использованы обозначения
b = |AC|, a = |BC|, c = |AB|, p = |BD|, q = |DC|.
что и требовалось доказать.
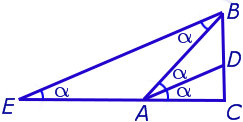
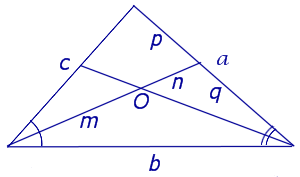
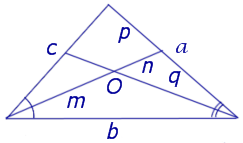
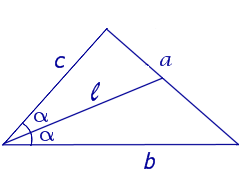
Следствие 2 . Рассмотрим рисунок 4, на котором изображены две биссектрисы треугольника, пересекающиеся в точке O .
Тогда справедлива формула:
что и требовалось доказать.
Теорема 2 . Рассмотрим рисунок 5, который практически совпадает с рисунком 2.
Тогда для длины биссектрисы справедлива формула:
Доказательство . Из рисунка 5 следует формула
Если воспользоваться этой формулой, то из подобия треугольников ADC и EBC , получаем:
что и требовалось доказать.
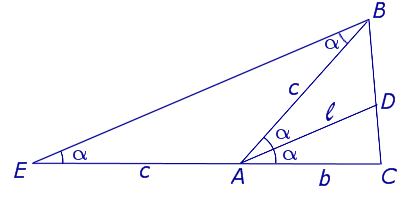
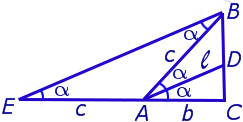
Теорема 3 . Длину биссектрисы треугольника (рис.6) можно найти по формуле:
Доказательство . Рассмотрим рисунок 6
откуда с помощью Теоремы 2 получаем:
что и требовалось доказать.
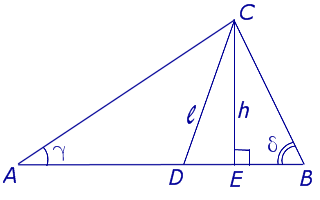
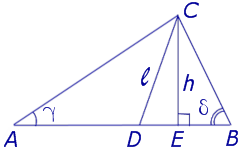
Задача . Из вершины C треугольника ABC (рис.7) проведена биссектриса CD и высота CE .
Доказать, что выполнено равенство:
Решение . Поскольку CD – биссектриса угла ACB , то
Поскольку CE – высота, то
что и требовалось доказать.
Из решения этой задачи вытекает простое следствие.
Следствие . Длины биссектрисы CD и высоты CE связаны следующей формулой:
Источник
Биссектриса треугольника онлайн
С помощю этого онлайн калькулятора можно найти биссектрису треугольника. Для нахождения длины биссектрисы треугольника введите длины сторон треугольника, выберите сторону, к которой проведена биссектриса и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Определение 1. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника (Рис.1).
 |
Биссектриса треугольника также называют биссектрисей угла треугольника или биссектрисей внутреннего угла треугольника.
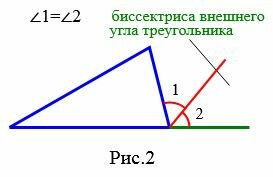
Биссектриса внешнего угла треугольника − это биссектриса угла, которая является смежным с внутренним углом треугольника (Рис.2).
 |
Любой треугольник имеет три биссектрисы.
Теорема 1. Биссектрисы треугольника пересекаются в одной точке.
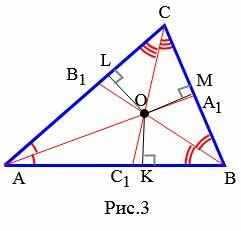 |
Доказательство. Проведем биссектрисы AA1, BB1 и обозначим через O точку их пересечения (Рис.3). Из точки O проведем перпендикуляры OK, OM и OL по сторонам треугольника ABC. По теореме 1 статьи Биссектриса угла. Свойства − OK=OL OK=OM. Следовательно OL=OM. Но последнее равенство означает, что точка O равноудалена от сторон AC и BC, т.е. находится на биссектрисе CC1 (Определение 2 статьи Биссектриса угла. Свойства).
Точка пересечения биссектрис треугольника называется инцентром треугольника. Инцентр треугольника является центром вписанной в треугольник окружности (Рис.4).
 |
Доказательство следует из теоремы 1, поскольку точка O равноудалена от сторон треугольника ABC и, следовательно, является центром окружности равной OK=OL=OM.
Длина биссектрисы треугольника
Рассмотрим треугольник на Рис.5.
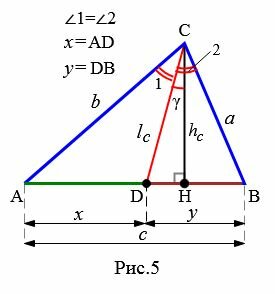 |
Длина биссектрисы треугольника можно вычислить следующими формулами:
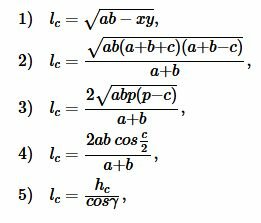 |
где p − полупериметр треугольника ABC, \( \small \gamma -\) угол между биссектрисой \( \small l_c\) и вершиной \( \small h_c:\)
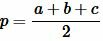 , , 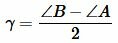 |
Доказательство. 1) Из теоремы Стюарта следует:
 | (1) |
А из теоремы о биссектрисе треугольника следует, что если lc является биссектрисей треугольника ABC (Рис.5), то имеет место следующее соотношение:
 | (2) |
Поскольку 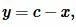
 | (3) |
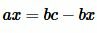 |
 | (4) |
 |
 | (5) |
Подставим (4) и (5) в (1):
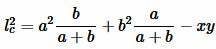  |
 . . | (6) |
 . . |
Доказательство. 2) Подставим (4) и (5) в (6):
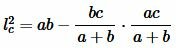 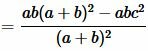 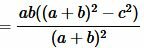 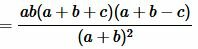 , , |
 . . | (7) |
 . . | (8) |
Доказательство. 3) Сделаем следующее обозначение:
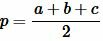 . . | (9) |
Сделаем преобразования формулы (7), учитывая (9):
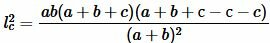 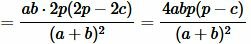 . . |
 . . | (10) |
Доказательство. 4) Для доказательства четвертой формулы, снова обратимся к рисунке Рис.5. Запишем формулы площадей треугольников ABC, ADC и BDC:
 , , |
 , , |
 . . |
Учитывая, что 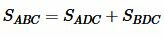
 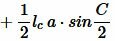 |
 . . |
 . . | (11) |
Для \( \small \sin C \) применим формулу синуса двойного угла:
 . . | (12) |
Подставляя (12) в (11) получим:
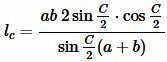 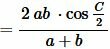 . . |
 . . | (13) |
Доказательство. 5) Докажем пятую формулу. Из вершины C проведена вершина CH. Имеем прямоугольный треугольник CHD, для которого имеет место следующее равенство:
 . . |
 . . |
Остается показать, что 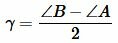
Поскольку биссектриса lc делит угол C пополам, то:
Источник