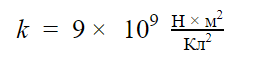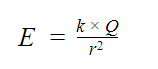Что такое напряженность электрического поля вывести формулу

Напряженность электрического поля

О чем эта статья:

8 класс, 10 класс

Что такое электрическое поле

Однажды Бенджамин Франклин, чей портрет можно увидеть на стодолларовой купюре, запускал воздушного змея во время дождя с грозой. Столь странное занятие он выбрал не просто так, а с целью исследования природы молнии. Заметив, что на промокшем шнуре волоски поднялись вверх (т. е. он наэлектризовался), Франклин хотел прикоснуться к металлическому ключу. Но стоило ему приблизить палец, раздался характерный треск и появились искры. Сработало электрическое поле.

Это случилось в середине XVIII века, но еще целое столетие ученые не могли толком объяснить, как именно заряженные тела взаимодействуют друг с другом, не соприкасаясь. Майкл Фарадей первым выяснил, что между ними есть некое промежуточное звено. Его выводы подтвердил Джеймс Максвелл, который установил, что для воздействия одного такого объекта на другой нужно время, а значит, они взаимодействуют через «посредника».

В современной физике электрическое поле — это некая материя, которая возникает между заряженными телами и обусловливает их взаимодействие. Если речь идет о неподвижных объектах, поле называют электростатическим.

Объекты, несущие одноименные заряды, будут отталкиваться, а тела с разноименными зарядами — притягиваться.

Определение напряженности электрического поля

Для исследования электрического поля используются точечные заряды. Давайте выясним, что это такое.

Точечным зарядом называют такой наэлектризованный объект, размерами которого можно пренебречь, поскольку он слишком мал в сравнении с расстоянием, отделяющим этот объект от других заряженных тел.

Теперь поговорим непосредственно о напряженности, которая является одной из главных характеристик электрического поля. Это векторная физическая величина. В отличие от скалярных она имеет не только значение, но и направление.

Для того, чтобы исследовать электрическую напряженность, нужно в поле заряженного тела q₁ поместить еще один точечный заряд q₂ (допустим, они оба будут положительными). Со стороны q₁ на q₂ будет действовать некая сила. Очевидно, что для расчетов нужно иметь в виду как значение данной силы, так и ее направление, то есть вектор.

Напряженность электрического поля — это показатель, равный отношению силы, действующей на заряд в электрическом поле, к величине этого заряда.

Напряженность является силовой характеристикой поля. Она говорит о том, как сильно влияние поля в данной точке не только на другой заряд, но также на живые и неживые объекты.

Единицы измерения и формулы

Из указанного выше определения понятно, как найти напряженность электрического поля в некой точке:

E = F / q, где F — действующая на заряд сила, а q — величина заряда, расположенного в данной точке.

Если нужно выразить силу через напряженность, мы получим следующую формулу:

F = q × E

Направление напряженности электрического поля всегда совпадает с направлением действующей силы. Если взять отрицательный точечный заряд, формулы будут работать аналогично.

Поскольку сила измеряется в ньютонах, а величина заряда — в кулонах, единицей измерения напряженности электрического поля является Н/Кл (ньютон на кулон).

Принцип суперпозиции

Допустим, у нас есть несколько зарядов, которые перекрестно взаимодействуют и образуют общее поле. Чему равна напряженность электрического поля, создаваемого этими зарядами?

Было установлено, что общая сила воздействия на конкретный заряд, расположенный в поле, является суммой сил, действующих на данный заряд со стороны каждого тела. Из этого следует, что и напряженность поля в любой взятой точке можно вычислить, просуммировав напряжения, создаваемые каждым зарядом в отдельности в той же точке (с учетом вектора). Это и есть принцип суперпозиции.

Это правило корректно для любых полей, за некоторыми исключениями. Принцип суперпозиции не соблюдается в следующих случаях:

расстояние между зарядами очень мало — порядка 10 -15 м;

речь идет о сверхсильных полях с напряженностью более 10 20 в/м.

Но задачи с такими данными выходят за пределы школьного курса физики.

Напряженность поля точечного заряда

У электрического поля, создаваемого точечным зарядом, есть одна особенность — ввиду малой величины самого заряда оно очень слабо влияет на другие наэлектризованные тела. Именно поэтому такие «точки» используют для исследований.

Но прежде чем рассказать, от чего зависит напряженность электрического поля точечного заряда, рассмотрим подробнее, как взаимодействуют эти заряды.

Закон Кулона

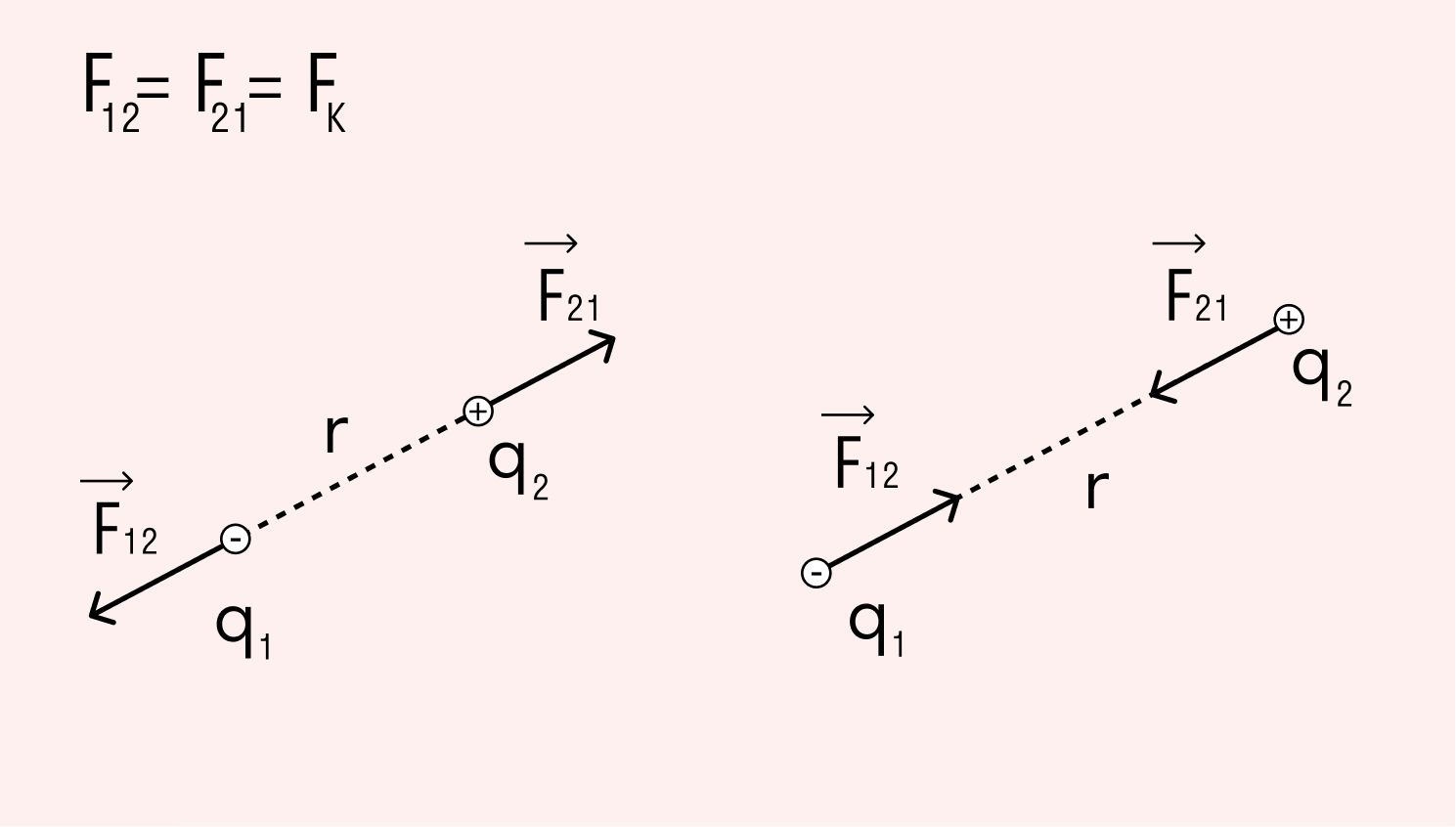
Предположим, в вакууме есть два точечных заряженных тела, которые статично расположены на некотором расстоянии друг от друга. В зависимости от одноименности или разноименности они могут притягиваться либо отталкиваться. В любом случае на эти объекты воздействуют силы, направленные по соединяющей их прямой.

Закон Кулона

Модули сил, действующих на точечные заряды в вакууме, пропорциональны произведению данных зарядов и обратно пропорциональны квадрату расстояния между ними.

Силу электрического поля в конкретной точке можно найти по формуле: 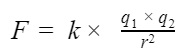где q₁ и q₂ — модули точечных зарядов, r — расстояние между ними.

В формуле участвует коэффициент пропорциональности k, который был определен опытным путем и представляет собой постоянную величину. Он обозначает, с какой силой взаимодействуют два тела с зарядом 1 Кл, расположенные на расстоянии 1 м.

Учитывая все вышесказанное, напряжение электрического поля точечного заряда в некой точке, удаленной от заряда на расстояние r, можно вычислить по формуле:

Итак, мы выяснили, что называется напряженностью электрического поля и от чего зависит эта величина. Теперь посмотрим, как она изображается графическим способом.

Линии напряженности

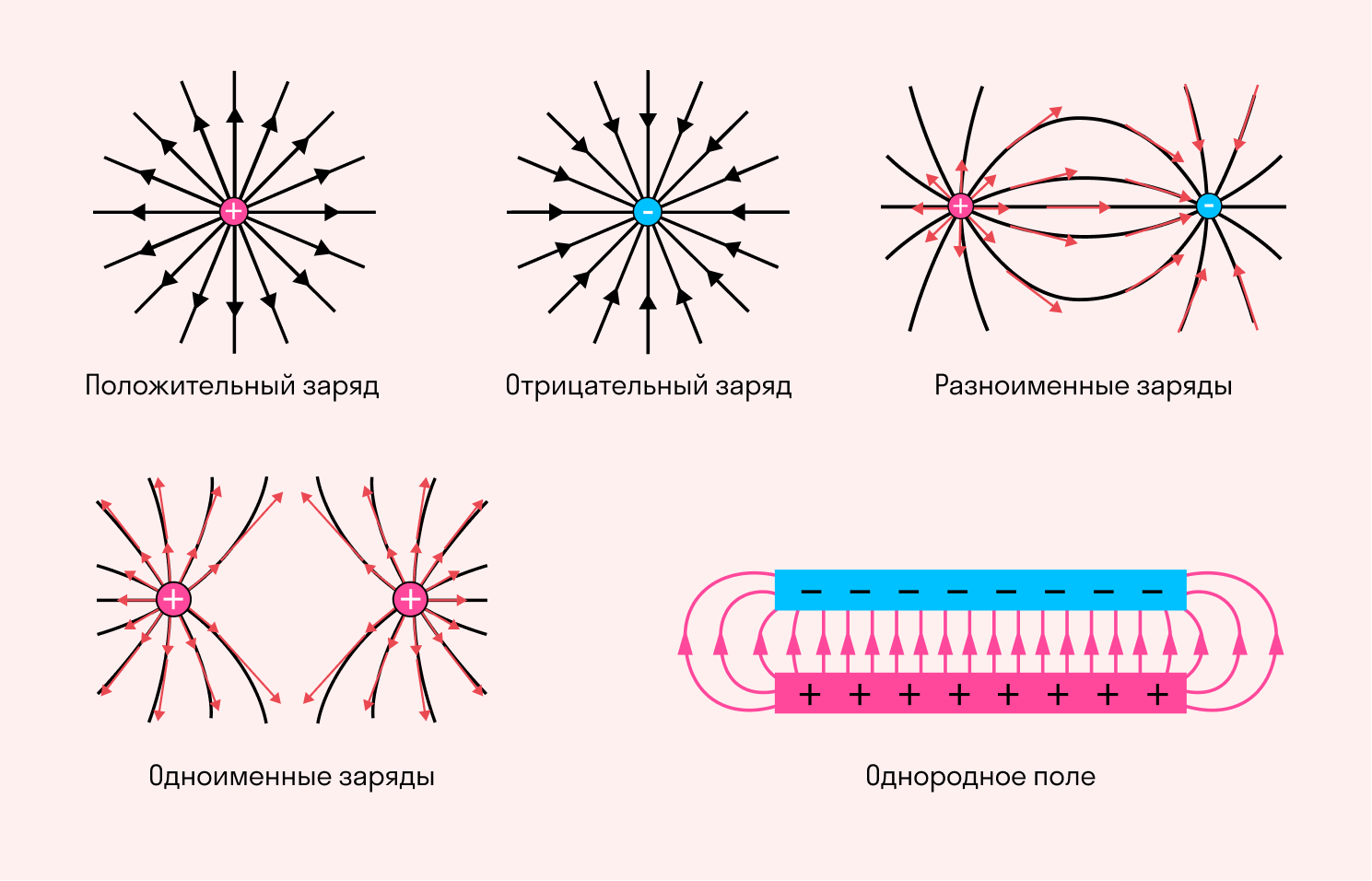
Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.

Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля.

При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.

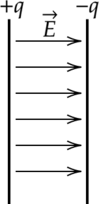
Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.

Источник

Формула напряженности электрического поля

Определение и формула напряженности электрического поля

Вектор напряженности $\bar$ – это силовая характеристика электрического поля. В некоторой точке поля, напряженность равна силе, с которой поле действует на единичный положительный заряд, размещенный в указанной точке, при этом направление силы и напряженности совпадают. Математическое определение напряженности записывается так:

где $\bar$ – сила, с которой электрическое поле действует на неподвижный, «пробный», точечный заряд q, который размещают в рассматриваемой точке поля. При этом считают, что «пробный» заряд мал на столько, что не искажает исследуемого поля.

Если поле является электростатическим, то его напряженность от времени не зависит.

Если электрическое поле является однородным, то его напряженность во всех точках поля одинакова.

Графически электрические поля можно изображать при помощи силовых линий. Силовыми линиями (линиями напряженности) называют линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности в этой точке поля.

Принцип суперпозиции напряженностей электрических полей

Если поле создано несколькими электрическими полями, то напряженность результирующего поля равна векторной сумме напряженностей отдельных полей:

Допустим, что поле создается системой точечных зарядов и их распределение непрерывно, тогда результирующая напряженность находится как:

интегрирование в выражении (3) проводят по всей области распределения заряда.

Напряженность поля в диэлектрике

Напряженность поля $\bar$ в диэлектрике равна векторной сумме напряженностей полей, создаваемых свободными зарядами $\bar_0$ и связанными (поляризационными зарядами) $\bar_p$:

В том случае, если вещество, которое окружает свободные заряды однородный и изотропный диэлектрик, то напряженность $\bar$ равна:

где $\varepsilon$ – относительная диэлектрическая проницаемость вещества в исследуемой точке поля. Выражение (5) обозначает то, что при заданном распределении зарядов напряженность электростатического поля в однородном изотропном диэлектрике меньше, чем в вакууме в $\varepsilon$ раз.

Напряженность поля точечного заряда

Напряженность поля точечного заряда q равна:

где $\varepsilon_<0>=8,85 \cdot 10^<-12>$ Ф/м (система СИ) — электрическая постоянная.

Связь напряженности и потенциала

В общем случае напряженность электрического поля связана с потенциалом как:

где $\varphi$ – скалярный потенциал, $\bar$ – векторный потенциал.

Для стационарных полей выражение (7) трансформируется в формулу:

Единицы измерения напряженности электрического поля

Основной единицей измерения напряженности электрического поля в системе СИ является: [E]=В/м(Н/Кл)

Примеры решения задач

Задание. Каков модуль вектора напряженности электрического поля $\bar$ в точке, которая определена радиус- вектором $\bar_<2>=7 \bar+3 \bar$ (в метрах), если электрическое поле создает положительный точечный заряд (q=1Кл), который лежит в плоскости XOY и его положение задает радиус вектор $\bar_<1>=\bar-5 \bar$, (в метрах)?

Решение. Модуль напряжения электростатического поля, которое создает точечный заряд, определяется формулой:

r- расстояние от заряда, создающего поле до точки в которой ищем поле.

Из формулы (1.2) следует, что модуль $\bar$ равен:

Подставим в (1.1) исходные данные и полученное расстояние r, имеем:

Ответ. $E=9 \cdot 10^<7>\left(\frac\right)$

Формула напряженности электрического поля не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Запишите выражение для напряженности поля в точке, которая определена радиус – вектором $\bar$, если поле создается зарядом, который распределен по объему V с плотностью $\rho=\rho(r)$ .

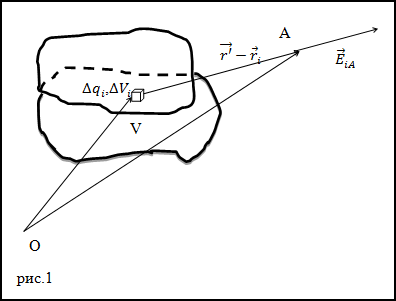
Решение. Сделаем рисунок.

Проведем разбиение объема V на малые области с объемами $\Delta V_$ заряды этих объемов $\Delta q_$, тогда напряженность поля точечного заряда в точке А (рис.1) будет равна:

Для того чтобы найти поле, которое создает все тело в точке А, используем принцип суперпозиции:

где N – число элементарных объемов, на которые разбивается объем V.

Плотность распределения заряда можно выразить как:

Из выражения (2.3) получим:

$\Delta q_=\rho\left(\bar_\right) \Delta V_(2.4)$

Подставим выражение для элементарного заряда в формулу (2.2), имеем:

Так ка распределение зарядов задано непрерывное, то если устремить $\Delta V_i$ к нулю, то можно перейти от суммирования к интегрированию, тогда:

Источник

Электрическое поле. Напряженность. Принцип суперпозиции

Электрическое поле. Напряженность электрического поля. Линии напряженности электрического поля (силовые линии). Однородное электрическое поле. Напряженность электростатического поля точечного заряда. Принцип суперпозиции полей. Теорема Гаусса. Электростатическое поле равномерно заряженных плоскости, сферы и шара.

Электрическое поле представляет собой векторное поле, существующее вокруг тел или частиц, обладающее электрическим зарядом, а также возникающее при изменении магнитного поля.

Напряженность электрического поля — это отношение вектора силы \(\vec\) , с которой поле действует на пробный заряд \(q\) , к самому пробному заряду с учетом его знака.

Единицы измерения: \(\displaystyle [\text<В>/\text<м>]\) (вольт на метр).

всегда начинаются на положительных зарядах и заканчиваются на отрицательных.

— такое поле в данной области пространства. если вектор напряженности поля одинаков в каждой точке области.

При равномерном распределении электрического заряда \(q\) по поверхности площади \(S\) поверхностная плотность заряда \(\displaystyle \sigma\) постоянна и равна

Напряженность электростатического поля точечного заряда Q в точке A, удаленной на расстояние \(r\) от заряда \(Q\) , определяется формулой:

Принцип суперпозиции полей

Пусть заряды \(\displaystyle q_1, q_2, q_3. , q_n\) по отдельности создают в данной точке поля \(\vec_1\) , \(\vec_2\) . \(\vec_n\) . Тогда система этих зарядов создает в данной точке поле \(\vec\) , равное векторной сумме напряженностей полей отдельных зарядов.

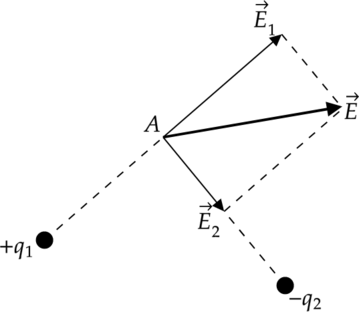
Разберемся, что такое принцип суперпозиции на примере электрического поля. Благодаря ему, можно найти напряженность двух точечных зарядов, в каждой точке поля \(А\) . Рассмотрим рисунок:

здесь видно, что для нахождения направления результирующего вектора \(\vec\) , нужно сложить вектора \(\vec_1\) и \(\vec_2\) по правилу параллелограмма. Это и есть принцип суперпозиции.

Поток вектора напряженности электростатического поля \(\vec\) через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную \(\varepsilon_0\) .

Заряженная плоскость

Её электрическое поле однородно, то есть его напряжённость одинакова на любом расстоянии от плоскости, линии напряжённости параллельны. По теореме Гаусса:

Заряженная сфера

Рассмотрим электрическое поле равномерно заряженной сферы. Поток напряжённости через любую замкнутую поверхность внутри сферы равен нуля, так как внутри этой поверхности нет заряда. Отсюда следует, что внутри сферы напряжённость равна нулю.

Проведём сферическую поверхность радиусом \(r>R\) . Пусть её заряд равен \(q\) . По теореме Гаусса:

Заряженный шар

Рассмотрим электрическое поле равномерно заряженного шара. Напомним, что объём шара равен \(V=\dfrac<4><3>\pi R^3\) . Тогда его заряд \(q=\dfrac<4><3>\pi R^3\rho\) . Напряжённость поля вне шара \(r>R\) можно найти так же, как и вне сферы:

Для нахождения напряжённости внутри шара применим теорему Гаусса для сферической поверхности радиусом \(r . По теореме Гаусса:

Источник

Читайте также:  При каких температурах можно стирать пуховик